SIAM News Blog
Research

A Batch-based, Stochastic Algorithm for Large-scale Ptychography

By
<strong>Figure 1.</strong> Schematic of a ptychography experiment. Figure courtesy of [1].
Figure 1. Schematic of a ptychography experiment. Figure courtesy of [1].

Ptychography is a popular imaging technique that finds use in diverse scientific applications, including biology [5], optics [7], and crystallography [3]. By combining both coherent diffractive imaging and scanning transmission electron microscopy, ptychographic experiments scan a coherent beam across an object of interest to “take a picture” of it (see Figure 1). The scans may have overlapping positions with each other, yielding a phaseless measurement that looks nothing like the object in question. However, we can use the collective set of measurements to recover the image, i.e., the phase of the object. Mathematically, we aim to solve the following problem:

\[\begin{aligned} &\textrm{To find} \; \omega \in \mathbb{C}^{m^2} \enspace \textrm{and} \enspace z \in \mathbb{C}^{n^2}\\ &\textrm{such that} \; |\mathcal{F}(\omega \circ S_j(z)) |^2 = d_j, \; j=1, \ldots, N. \end{aligned} \tag1\]

Here, \(z \in \mathbb{C}^{n^2}\) is the object of interest with \(n \times n\) pixels and \(\omega \in \mathbb{C}^{m^2}\) is the localized two-dimensional (2D) probe with \(m \times m\) pixels, where typically \(m < n\). The set of phaseless measurements is denoted by \(\{d_j\}_{j=1}^N\) such that \(d_j = |\mathcal{F} (\omega \circ S_j (z))|^2\), where \(\mathcal{F}\) is the 2D discrete Fourier operator and \(S_j: \mathbb{C}^{n^2} \rightarrow \mathbb{C}^{m^2}\) is a binary mask that represents an \(m \times m\) window over the image \(z\) at scanning step \(j\).

&lt;strong&gt;Figure 2.&lt;/strong&gt; A complex sample image \(z = |z|e^{i\theta}\) of size \(350 \times 350\). &lt;strong&gt;2a.&lt;/strong&gt; The magnitude image \(|z|\). &lt;strong&gt;2b.&lt;/strong&gt; The phase image \(\theta\); the bottom right corner shows the image’s probe \(\omega\) of size \(256 \times 256\). &lt;strong&gt;2c.&lt;/strong&gt; The scanning pattern of the numerical experiments. Figure courtesy of [1].
Figure 2. A complex sample image \(z = |z|e^{i\theta}\) of size \(350 \times 350\). 2a. The magnitude image \(|z|\). 2b. The phase image \(\theta\); the bottom right corner shows the image’s probe \(\omega\) of size \(256 \times 256\). 2c. The scanning pattern of the numerical experiments. Figure courtesy of [1].

Large-scale ptychography requires a substantial number of phaseless measurements to reconstruct a high-resolution image. Unfortunately, the simultaneous processing of all of these measurements can be computationally demanding in both memory and time. To mitigate this issue, we developed a batch-based, stochastic algorithm for an existing optimization model [2]. This algorithm randomly samples a small number of measurements each iteration with which perform an image reconstruction. Unlike a deterministic algorithm that processes all measurements during every iteration, our proposed algorithm detailed in [1] is computationally efficient and avoids bad reconstructions — which is especially important since \((1)\) can have multiple reconstructed solutions.

&lt;strong&gt;Figure 3.&lt;/strong&gt; Image reconstruction of the magnitude and phase components. Figure courtesy of the authors.
Figure 3. Image reconstruction of the magnitude and phase components. Figure courtesy of the authors.

We compare the stochastic algorithm and its deterministic, full-batch counterpart via a numerical example. The complex-valued image \(z = |z|e^{i \theta}\) in Figure 2 consists of the magnitude image \(|z|\) (see Figure 2a) and the phase image \(\theta\) (see Figure 2b). The probe \(\omega\) in the bottom right corner of Figure 2b scans the complex-valued image. During numerical experiments, we repeatedly scan the image until we have \(N=100\) phaseless measurements. Figure 2c depicts the scanning pattern of the probe.

To increase the difficulty of the image reconstruction process, we add Gaussian noise to the phaseless measurements. We then run both the stochastic and deterministic algorithms up to 600 total epochs, where each epoch represents one complete pass with all phaseless measurements. For the stochastic algorithm, we examine batch sizes \(b= 5, 10, 20,\) and \(50\).

&lt;strong&gt;Figure 4.&lt;/strong&gt; Structural similarity index measure (SSIM) values of the reconstruction of the magnitude and phase components. Figure courtesy of the authors.
Figure 4. Structural similarity index measure (SSIM) values of the reconstruction of the magnitude and phase components. Figure courtesy of the authors.

Figure 3 illustrates the reconstruction results of our proposed stochastic algorithm and the deterministic algorithm. To measure reconstruction quality, we use the structural similarity index measure (SSIM) for both the magnitude and phase components (see Figure 4). The stochastic and deterministic algorithms reconstruct the magnitude component with comparable quality, although the stochastic algorithm’s SSIM is lower by at most four percent. On the other hand, the stochastic algorithm more clearly reconstructs the phase component, with a SSIM of at least 73 percent; the deterministic algorithm fails to recover the left half of the phase component. Overall, the stochastic algorithm successfully reconstructs the magnitude and phase components with satisfactory quality, whereas the deterministic algorithm only succeeds in reconstructing the magnitude component.

&lt;strong&gt;Figure 5.&lt;/strong&gt; Magnitude and phase structural similarity index measures (SSIMs) versus computational time (in seconds) for the blind algorithms. Each algorithm runs for 600 epochs. Figure courtesy of the authors.
Figure 5. Magnitude and phase structural similarity index measures (SSIMs) versus computational time (in seconds) for the blind algorithms. Each algorithm runs for 600 epochs. Figure courtesy of the authors.

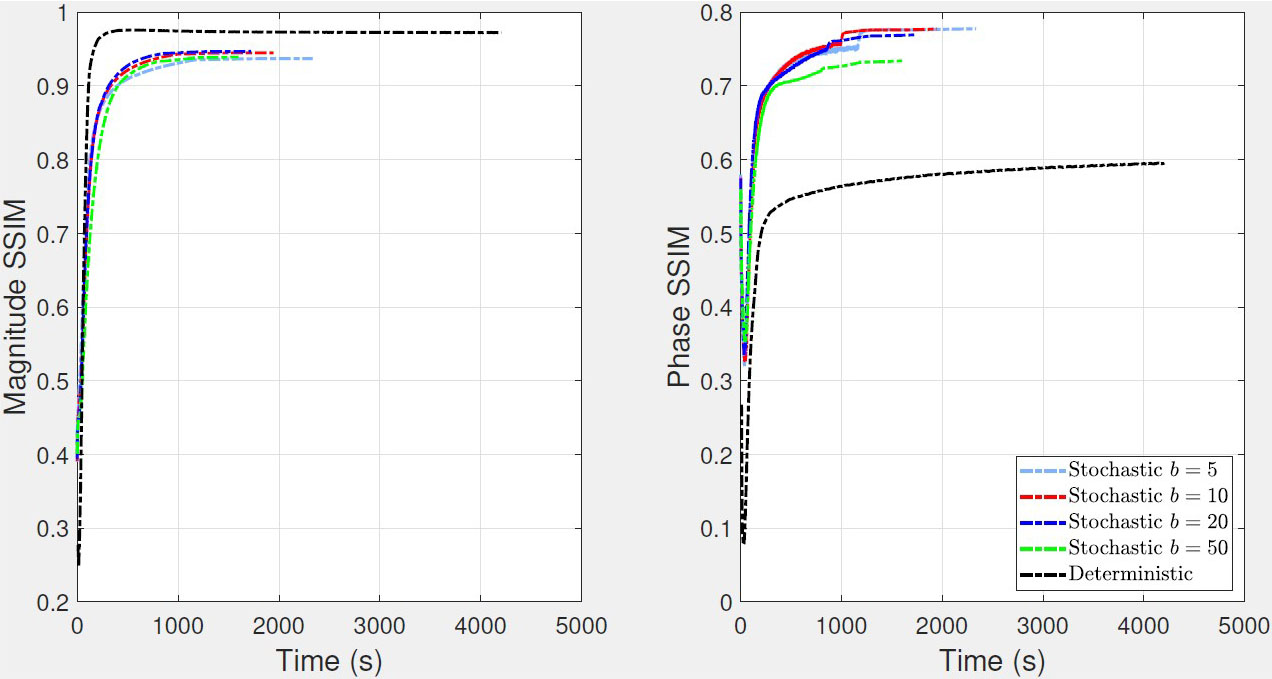
Figure 5 displays the computational efficiency of the stochastic and deterministic algorithms. The stochastic algorithm completes its run in 1,500 to 2,500 seconds, while the deterministic algorithm requires more than 4,000 seconds (i.e., over an hour). In short, the stochastic algorithm may be roughly two times faster than its deterministic counterpart, especially when the batch size is \(b \geq 10\). Moreover, running all 600 epochs may be unnecessary for this algorithm; running the stochastic algorithm for only 500 seconds still results in a magnitude SSIM of at least 90 percent and a phase SSIM of at least 70 percent. Increasing the algorithm’s batch size does improve its speed, but only by a few hundred seconds.

Here, we demonstrated the potential of our stochastic algorithm in large-scale image ptychography. The proposed algorithm is computationally efficient and yields satisfactory image reconstructions. In the future, we hope to improve the stochastic algorithm by incorporating variance reduction, such as the stochastic variance reduced gradient method [4] or StochAstic Recursive grAdient algoritHm (SARAH) reduction technique [6].

Kevin Bui delivered a minisymposium presentation on this research at the 2023 SIAM Conference on Computational Science and Engineering (CSE23), which took place in Amsterdam, the Netherlands, last year. He received funding to attend CSE23 through a SIAM Student Travel Award. To learn more about Student Travel Awards and submit an application, visit the online page. 

SIAM Student Travel Awards are made possible in part by the generous support of our community. To make a gift to the Student Travel Fund, visit the SIAM website. 

Zichao (Wendy) Di also delivered a minisymposium presentation on this research at the 2023 SIAM Conference on Optimization, which took place in Seattle, Wash., last year.

References
[1] Bui, K., & Di, Z.W. (2024). A stochastic ADMM algorithm for large-scale ptychography with weighted difference of anisotropic and isotropic total variation. Inverse Probl., 40(5), 055006.
[2] Chang, H., Lou, Y., Ng, M.K., & Zeng, T. (2016). Phase retrieval from incomplete magnitude information via total variation regularization. SIAM J. Sci. Comput., 38(6), A3672-A3695.
[3] De Caro, L., Altamura, D., Arciniegas, M., Siliqi, D., Kim, M.R., Sibillano, T., … Giannini, C. (2016). Ptychographic imaging of branched colloidal nanocrystals embedded in free-standing thick polystyrene films. Sci. Rep., 6(1), 19397.
[4] Johnson, R., & Zhang, T. (2013). Accelerating stochastic gradient descent using predictive variance reduction. In NIPS'13: Proceedings of the 26th international conference on neural information processing systems (pp. 315-323). Lake Tahoe, NV: Curran Associates Inc.
[5] Marrison, J., Räty, L., Marriott, P., & O’Toole, P. (2013). Ptychography – A label free, high-contrast imaging technique for live cells using quantitative phase information. Sci. Rep., 3(1), 2369.
[6] Nguyen, L.M., Liu, J., Scheinberg, K., & Takáč, M. (2017). SARAH: A novel method for machine learning problems using stochastic recursive gradient. In 34th international conference on machine learning (ICML 2017) (pp. 2613-2621). Sydney, Australia: Proceedings of Machine Learning Research.
[7] Shechtman, Y., Eldar, Y.C., Cohen, O., Chapman, H.N., Miao, J., & Segev, M. (2015). Phase retrieval with application to optical imaging: A contemporary overview. IEEE Signal Process. Mag., 32(3), 87-109.

About the Authors

Kevin Bui

Senior research engineer, Samsung Research America

Kevin Bui is a senior research engineer at Samsung Research America. He holds a Ph.D. in mathematics from the University of California, Irvine. Bui’s research focuses on the development of algorithms and models for image processing, especially image restoration and segmentation. 

Zichao (Wendy) Di

Computational mathematician, Argonne National Laboratory

Zichao (Wendy) Di is a computational mathematician at Argonne National Laboratory with a joint appointment in the Mathematics and Computer Science Division and X-ray Science Division. Her research explores the generalization of multilevel methods for the solution of optimization problems like vector quantization and optimal control, inverse problems, and information integration and multimodal data analysis.