A Bifurcation in Moore’s Law?

According to the TOP500 list, the speed of the world’s fastest computer has increased over the past 25 years from \(10^{12}\) to \(10^{18}\) flops — from teraflops to exaflops, or six orders of magnitude.

What about the desktop machine that I actually use? It’s gone from around \(10^8\) to \(10^{11}\) flops. For example, the computation that was originally reported to take one second on page 178 of Numerical Linear Algebra [1] now takes me half a millisecond. That’s just three orders of magnitude.

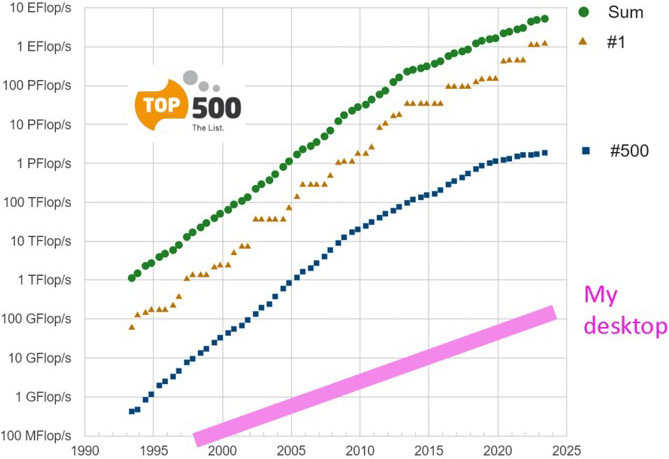
It would seem that some kind of Moore’s law bifurcation is taking place between the ordinary and the high end of computing. Computational scientists talk exaflops, but most of us are living teraflops.

The hardware basis of the bifurcation is clear: the top machines have thousands or even millions of processors, and most of us don’t work in that mode. But I’m more interested in the scientific and sociological aspects. Throughout my career as a numerical analyst, I’ve had the sense that although many of us don’t use the top machines, that kind of computing was our ultimate motivation. Now I’m not so sure. High-performance computing is certainly indispensable in some applications, but is it becoming a less accurate model of the heart of computational science? 

I mentioned these thoughts during a recent “26 years at Oxford” valedictory talk to the Numerical Analysis Group at the University of Oxford. I showed the plot in Figure 1 and asked, “How many of you are playing the high-performance game?” Just one person raised their hand out of roughly 60 attendees. I’m guessing that more hands might have gone up in an American audience, but still a small number. 

If others have thoughts about this trend, I’d be glad to hear from you. 

References

[1] Trefethen, L.N., & Bau, D. (1997). Numerical linear algebra (1st ed.). Philadelphia, PA: Society for Industrial and Applied Mathematics.