A Lagrange Multiplier Problem Without Multipliers

Here is a calculus-free solution of the standard vector calculus problem:

Minimize

\[\begin{equation}\tag{1} f (x, y, z) = ax^2 + by^2 + cz^2 \end{equation}\]

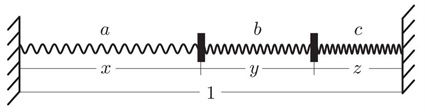
subject to \(g (x, y, z) = x + y + z = 1\), where \(a\), \(b\), and \(c\) are positive constants.Solution. Figure 1 shows three springs with Hooke’s constants \(a\), \(b\), and \(c\), connected end to end. If each spring is assumed to have relaxed length of zero, (1) gives twice the potential energy of the system. If this energy is minimal, the system is in equilibrium and the tensions of the springs are thus equal:

\[ax = by = cz. \tag2 \]

We have solved the problem by showing that the minimizing lengths should be in inverse proportion to the corresponding coefficients (“the stiffer, the shorter”), implying

\[x = \frac{\frac{1}{a}}{\frac{1}{a} + \frac{1}{b} + \frac{1}{c}},\]

with similar expressions for \(y\) and \(z\). 

We can compare this with the “standard” solution: Lagrange’s necessary condition for the minimum

\[\begin{equation}\tag{3}
\nabla f = \lambda \nabla g                  
\end{equation}\]

yields

\[\begin{equation}\langle 2ax, 2by, 2cz \rangle =  \lambda \langle 1, 1, 1 \rangle,
\end{equation}\]

which is the same as our result (2) (without the physical interpretation).

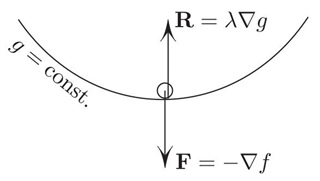
Incidentally, Lagrange’s method (3)––for general functions \(f\) and \(g\)––admits a simple static interpretation. Consider a particle constrained frictionlessly to the surface \(g =\) constant and subject to the force field \(\boldsymbol{\mathrm{F}} = –\nabla  f\) in space; we thus interpret \(f\) as the potential energy, which we are trying to minimize. But minimality at some \(M\) means that \(M\) is an equilibrium, where \(\boldsymbol{\mathrm{F}}\) must be cancelled by the reaction force \(\boldsymbol{\mathrm{R}}\): 

\[\begin{equation}\tag{4}
\boldsymbol{\mathrm{F}} = –\boldsymbol{\mathrm{R}}.    
\end{equation}\]

Without friction, the reaction is normal to the surface: \(\boldsymbol{\mathrm{R}} = \lambda \nabla g\), and (4) is the same as (3). The Lagrange condition (3) is thus a special case of Newton’s first law. 

Acknowledgments: The work from which these columns are drawn is funded by NSF grant DMS-1412542.