A Mathematical Model to Support Hospital Workflow Management During a Pandemic
As with all pandemics, the worldwide spread of COVID-19 is significantly hindering patient flow management and severely straining hospital resources. Therefore, some healthcare professionals must make difficult decisions regarding patient care and resource allocation. While checklists for patient triage do exist, the dynamics of pandemics make efficient execution of these lists especially challenging. Senior management thus requires a tool that facilitates end-to-end demand visibility to identify and predict hospital bed constraints.
Multiple governmental and private agencies have focused on the creation of dashboards to supply the general public with assessments of COVID-19. A significant amount of literature concerning mathematical models in epidemiology provides a rigorous framework for the prediction of COVID-19 dynamics [9, 10]. However, providing the necessary information at the local hospital scale to optimize the management of patient workflow is complex, primarily because researchers still do not fully understand the disease. Every hospital must therefore adapt to COVID-19’s daily changes. As guidelines take time to implement, following the most up-to-date information yields significant variety in clinical practices.
The Appropriate Data Set and Agile Mathematical Modeling
The French government has released records of most public hospitals around the country during the COVID-19 crisis. This file reveals the number of patients in hospitals, the number of patients in the intensive care unit (ICU), the number of patients that are recovered and discharged, and the number of patients that have died in a medical institution. These numbers are updated daily and date back to March 18, 2020. Because of the sparsity of available data, we begin with a very simple model that reproduces the workflow to match the disease management of each patient (see Figure 1).
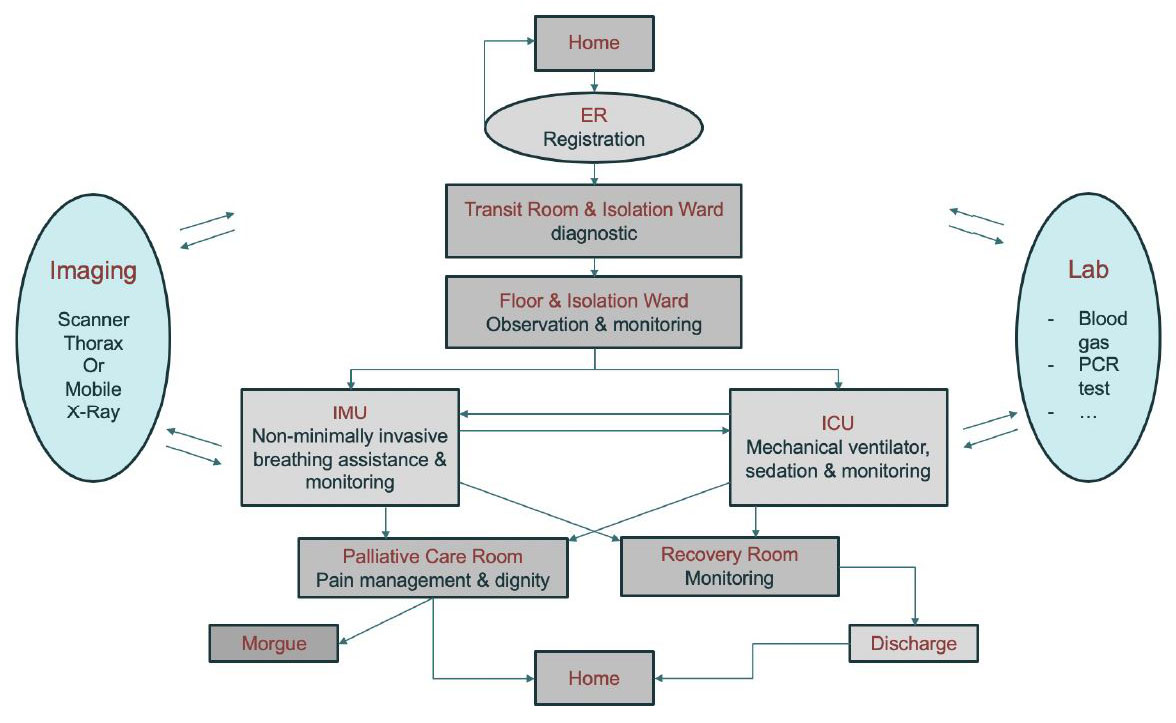
Most patients who require hospitalization are first placed on a medicine floor for further assessment and treatment. Non-invasive monitoring, as well as imaging and blood tests, help determine patients’ conditions and continue for the duration of their hospital stay. These resources—i.e., imaging and laboratory work—are shared by all patients in the hospital and may slow down the process when overwhelmed with users. Some people who receive medical attention do well with conservative management techniques and are discharged after only a few days. Other patients’ health conditions may deteriorate, necessitating a move to the intermediate care unit (IMU) for additional care or the ICU for ongoing monitoring and sometimes mechanical ventilation.
The IMU and ICU require extensive supplies and resources. Ventilators are not the only limiting factor, as patients under mechanical ventilation need sedation and might be connected to additional systems that handle organ failure. We can add these constraints to our mathematical model with no technical difficulties due to a bottom-up workflow description [5, 8], as long as mandatory data is available. Additional levels of care for which we should account include recovery floor and palliative care floor — for patients who are not responsive to treatment. Of course, there are many exceptions and singularities to these standard paths. For example, a patient may go directly from admission to the ICU when his/her condition is too unstable. In some hospitals, recovering COVID-19 patients and palliative care patients might share the same floor. To summarize, we create a simple workflow graph that seeks to determine (i) the probability of a patient transitioning from one care unit to another and (ii) a statistical estimate of the patient’s duration of stay in each care unit.
The discrete model is stochastic, so we need to run many simulations to build a statistical estimate of quantities of interest. The number of unknown parameters that we must retrieve by fitting the data is relatively large. To avoid overfitting, researchers should devise a strategy that lowers the number of unknowns based on either clinical literature or validated hypothesis. One can retrieve the model’s unknown parameters via a stochastic optimization method since the workflow process—like that of the hospital—is discrete, noisy, and nonlinear.
A patient’s condition is dominated by the disease’s evolution. Furthermore, medical procedures accumulate delays; the durations of both biological and managerial processes are often described by a lognormal distribution with a long tail. This does not contradict the fact that a simple exponential distribution may not ideally depict a patient’s length of stay (LOS) in the hospital. Overall, LOS adds up the time distribution of every step in a Markov process and might be described at the convolution of each step’s probability distribution [7]. For example, we found it necessary to introduce an artificial two-phase decomposition of patient stay in the ICU to bypass the limitation of a single distribution that may not represent an adequate model of LOS in this unit, according to clinical studies [1].
To guide the optimization process, we employ a stability analysis of the model that ranks the most sensitive parameters, which should be estimated first. Performance depends on staff conditions and patient population, and the clinicians are clearly experienced with LOS in each step and provide an ad hoc window of time that we can fine-tune as a second pass of the algorithm. It is difficult to recover the true rate of death at the beginning of a new pandemic.
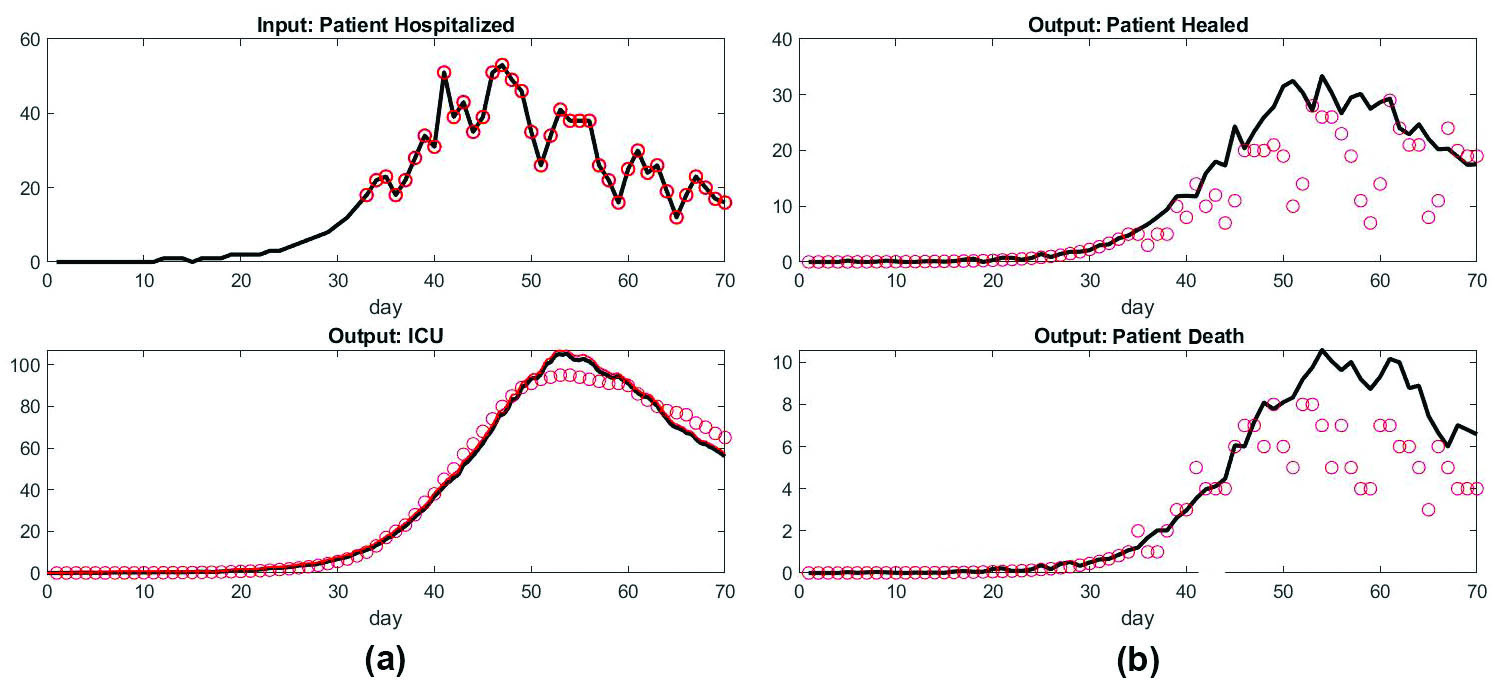
Our first, simplified model essentially requires the calibration of six parameters with a genetic algorithm that compares the model to France’s data set [4]. Figure 2 depicts the model’s success compared with France’s data set from March 18, 2020 to April 24, 2020.
Retrieving Information to Rationalize a Strategy
A manager may have the following simple yet essential questions. How many beds are needed on each floor and how many are available in the critical care unit? How many supplies should be ordered to support patient care and protect staff from infection? How long must the facility operate at maximum capacity, and is there enough staff to sustain this workload? One key factor involves anticipating the load of each care unit and required resources, either to match the patient increase or reallocate resources and begin rescheduling previously cancelled surgeries, for example.
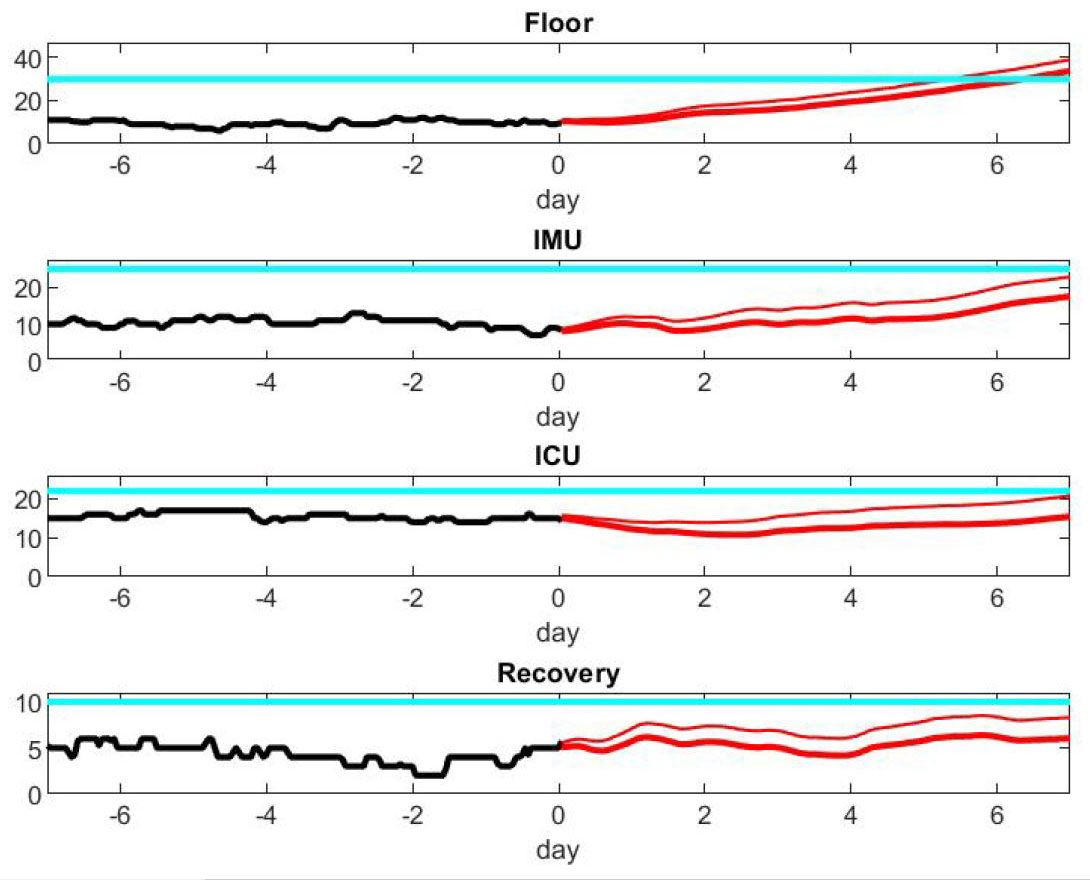
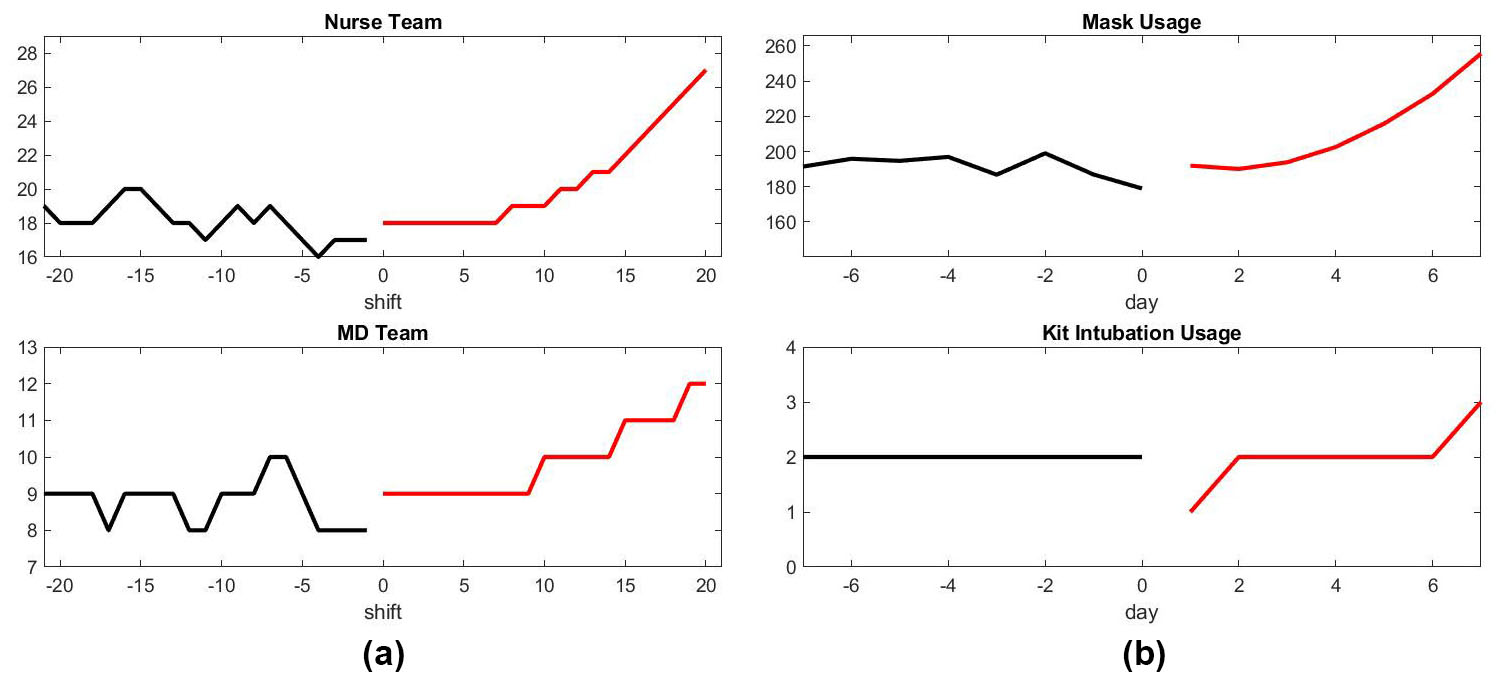
Our model could also allow managerial staff to make multiple decisions regarding patient care. Figure 5 compares patient output with and without a shortage of nurses. These results are speculative since it is difficult to quantify patient risk beyond published results [2, 3, 6]. We hope that new data accumulated during the COVID-19 crisis will provide the base for mathematical modeling to rigorously conduct this estimate in future works.
There are admittedly several limitations to our approach. Smaller hospitals yield less predictable outcomes, and the characteristics of the patient population that visits the emergency room change with time. Systematic testing would likely provide early diagnostics and impact the health system’s performance, as evidenced by the statistics of countries that adopted this strategy from the onset. Due to the heterogeneity of the patient population and disease patterns that depend heavily on patient characteristics, our next step to improve this model involves the inclusion of patients’ medical history from their electronic medical records. We plan to feed our model of hospital workflow with an epidemic model that maintains accuracy in the hospital’s ecosystem. Ultimately, we anticipate that the future of computational models in digital health during a pandemic will extensively include sociological and economical modeling components.
The figures in this article were provided by the authors.
Acknowledgments: We would like to thank Patrick Doolan for sharing his view on management and risk evaluation based on his experience in the energy sector.
References
[1] Esteban, A., Anzueto, A., Frutos, F., Alía, I., Brochard, L., Stewart, T.E., …, Tobin, M.J. (2002). Characteristics and outcomes in adult patients receiving mechanical ventilation. JAMA, 287(3), 345-55.
[2] Ferrer, J., Boelle, P.-Y., Salomon, J., Miliani, K., L’Heriteau, F., Astagneau, P., & Temime, L. (2014). Management of nurse shortage and its impact on pathogen dissemination in the intensive care unit. Epidem., 9, 62-69.
[3] Friedrich, B.U., & Hackmann, M.B. (2017). The returns to nursing: evidence from a parental leave program. (Working Paper No. 23174). National Bureau of Economic Research.
[4] Garbey, M., Joerger, G., Furr, S., & Fikfak, V. (2020). A model of workflow in the hospital during a pandemic to assist management. Preprint, medRxiv.
[5] Garbey, M., Joerger, G., Rambourg, J., Dunkin, B., & Bass, B. (2017). Multiscale modeling of surgical flow in a large operating room suite: understanding the mechanism of accumulation of delays in clinical practice. Proc. Comp. Sci., 108, 1863-1872.
[6] Hotchkiss, J.R., Strike, D.G., Simonson, D.A., Broccard, A.F., & Crooke, P.S. (2005). An agent-based and spatially explicit model of pathogen dissemination in the intensive care unit. Crit. Care Med., 33(1), 168.
[7] Ickowicz, A., & Sparks, R. (2016). Modelling hospital length of stay using convolutive mixtures distributions. Stat. Med., 36(1), 122-135.
[8] Joerger, G., Rambourg, J., Gaspard-Boulinc, H., Conversy, S., Bass, B.L., Dunkin, B.J., & Garbey, M. (2018). A cyber-physical system to improve the management of a large suite of operating rooms. ACM Trans. Cyber-Phys. Syst., 2(4), 34.
[9] Pujari, B.S., & Shekatkar, S. (2020). Multi-city modeling of epidemics using spatial networks: application to 2019-nCov (COVID-19) coronavirus in India. Preprint, medRxiv.
[10] Yang, C., & Wang, J. (2020). A mathematical model for the novel coronavirus epidemic in Wuhan, China. Math. Biosci. Eng., 17(3), 27082724.
About the Authors
Marc Garbey
Professor, Weill Cornell Medical College
Marc Garbey is a professor of computational science in Surgery at Houston Methodist Hospital and Weill Cornell Medical College, as well as a professor at Laboratoire des Sciences de l’Ingénieur pour l’Environnement – UMR CNRS 7356 at the University of La Rochelle, France.
Guillaume Joerger
Chief Technology Officer, ORintelligence, LLC
Guillaume Joerger is the chief technology officer at ORintelligence, LLC.
Shannon Furr
Information Systems Director, ORintelligence, LLC
Shannon Furr is the director of information systems at ORintelligence, LLC.
Vid Fikfak
Assistant Professor, University of Texas
Vid Fikfak is an assistant professor in the Department of Surgery at the University of Texas’ Health Sciences Center.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



