A Mathematical Tale of Fibers, Fluids, and Flagella

Under a microscope, a cell scoots along by its own power and hoovers up small crumbs of nutrition from the water around it. An example of such an organism is a choanoflagellate, which has a thin, whip-like appendage called a flagellum that controls its feeding and motion. While similarly proportioned apparatuses would be useless on a human scale, flagella are common among single-celled organisms like bacteria, the sometimes-toxic dinoflagellate algae, and even human sperm cells.

Motion in the microscopic world—particularly in fluids—involves an entirely different set of forces than those that govern macroscopic environments. Flagella operate efficiently under these forces and allow microscopic life to move around in fluids, where large viscous forces are present even in substances such as water. The motion of choanoflagellates and the way in which flexible fibers or strands of cells passively respond to liquid flow all constitute a set of complex problems with many potential applications in engineering and medicine.

“With the advent of microfluidic devices and computational technology, there has been an incredible resurgence in studies of the flow of tiny creatures at the microscale,” Lisa Fauci, an applied mathematician at Tulane University and a former president of SIAM, said. “There are possibilities of creating nanorobots that can be guided with external magnetic fields to break up blood clots or deliver drugs to a tumor.”

However, potential applications are not the only reason that Fauci is drawn to flexible fibers in fluids. “From the start, I was interested in problems in biological fluid dynamics,” she said. “What is really interesting and hard about fluid mechanics in a biological setting rather than an engineering setting [is that] the structure interacting with the fluid is elastic. It’s flexible, and its shape responds to the fluid flow.”

The fluids themselves in microscopic biological systems are also often complicated, regardless of whether the system of interest is blood, a reproductive tract, or the inside of a cell. Even free-swimming cells in water inhabit a world full of proteins and other fibrous biological detritus that certainly affects their movement. Fauci elaborated on these concepts during her Past President’s Address at the hybrid 2022 SIAM Annual Meeting, which took place in Pittsburgh, Pa., this July.

Fibers on Fibers

Fauci was among the pioneers who modeled microfluid environments via computers at a time when machines were becoming powerful enough to run increasingly realistic simulations. “There was interest in studying processes like sperm motility in the female reproductive tract and phytoplankton motion in the ocean through the lens of fluid mechanics,” she said. “I started working on these types of problems using computer simulations and new methodologies.”

In the microscopic regime dominated by viscous forces, Fauci and her collaborators often start with an incompressible Newtonian fluid that is governed mathematically by the linearized Navier-Stokes equations. This approximation results from the assumption that the fluid’s viscosity dominates over both its inertia and macroscopic external forces such as gravity. In fluid dynamics terms, this is the limit at which the Reynolds number—inversely proportional to viscosity—is zero. The resulting equations that govern the fluid are

\[-\nabla \rho+\mu\nabla^2\mathbf{u}+\mathbf{g}=0\]\[\nabla \cdot \mathbf{u}=0,\]

where \(\mathbf{u}\) is the velocity field for the fluid, \(\mu\) is the viscosity, \(\rho\) is the pressure, and \(\mathbf{g}\) is the force per unit volume from non-fluid influences like flagella.

The forms of the solutions to this equation naturally depend on forces \(\mathbf{g}\). To describe flexible fibers in Newtonian fluids, Fauci’s colleague at Tulane and frequent collaborator Ricardo Cortez introduced highly localized forces that can model both the fibers’ response and—where applicable—polymers that are suspended in the fluid:

\[\mathbf{g}=\mathbf{f} \varphi_{\epsilon}(r), \quad \textrm{where} \quad r=|x-x_0| \quad \textrm{and} \quad \varphi_{\epsilon}(r)=\frac{15\epsilon^4}{8\pi(r^2+\epsilon^2)^{7/2}}\]

is a regularized version of a Dirac delta function for small parameter \(\epsilon\). The exact solutions to the linearized Navier-Stokes equation with this force are

\[\mathbf{u}(x)=\mathbf{S}(x;\epsilon)\cdot \mathbf{f}=\frac{1}{8\pi\mu(r^2+\epsilon^2)^{3/2}}[\mathbf{f}(r^2+2\epsilon^2)+(\mathbf{f}\cdot (x-x_0))(x-x_0)],\]

where the matrix \(\mathbf{S}\) is a “regularized Stokeslet” [3]. The Newtonian fluid that these solutions describe serves as either the background for the simulation of passive fiber motion or the environment for a complex fluid of polymers.

For the latter, Fauci and her collaborators developed a mechanical model on a lattice that treats the molecules like springs and dashpots: a mechanical damper of the same type that prevents slamming in automatic door-closing mechanisms1 [4]. Cells lash their flagella within this two-layered background to move and feed (see Figure 1). “We’re using computational methods to model flagellar fibers that are moving through a fibrous network,” Fauci said. “So, fibers on fibers.”

Just Keep Swimming

The active fiber motion of flagella is not the only flexible-fiber system worth studying; microscopic biological environments are full of stringy proteins and even cells that are borne on microcurrents [1]. “Diatom chains are phytoplankton that are just swept around,” Fauci said. Phytoplankton—photosynthesizing, water-dwelling microorganisms—as a group are responsible for the production of roughly half of the planet’s oxygen. In other words, the passive motion of diatoms around the globe contributes to the chemistry of the atmosphere and oceans and links the microscopic to climate change.

Yet active flagella hold a special place in Fauci’s research program, and not just in the context of motion. Choanoflagellates sometimes anchor themselves to surfaces and use their flagella to snag food, reversing the same mechanisms that they originally evolved for swimming purposes [2]. This behavior, as well as their general shape, links choanoflagellates to the oldest surviving lineage of multicellular animals: the sponges (see Figure 2).

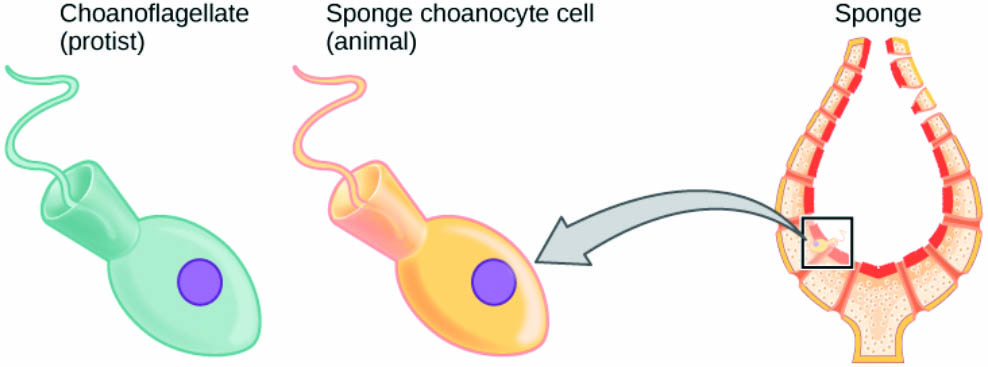
“As a mathematician, you have your toolkit with which you can solve these equations, figure out velocity fields and forces, and so forth,” Fauci said. “But it involves working with evolutionary biologists as well, who frame a very simple question [such as] is it better for me to be stuck to a wall? Or is it better for me to be free swimming?”

Choanoflagellates obviously do both, but sponges and more structurally complex animals forwent the single, free-swimming life in favor of communal grouping. More efficient food capture might have played a role in this development, in addition to the obvious advantages of collective safety in numbers. Such biological curiosities have driven Fauci as much as anything. “It’s really fabulous for me to spend my career in a mathematics department,” she said. “We can study whatever we want. It’s not ‘let’s get some technology out there.’ It’s basic science. It’s ‘how is this working?’”

¹ Interestingly, 19th-century physicist James Clerk Maxwell developed this type of mechanical lattice to describe the since-debunked “luminiferous aether.”

References

[1] Musielak, M., Karp-Boss, L., Jumars, P.A., & Fauci, L.J. (2009). Nutrient transport and acquisition by diatom chains in a moving fluid. J. Fluid Mech., 638, 401-421.
[2] Nguyen, H., Koehl, M.A.R., Oakes, C., Bustamante, G., & Fauci, L. (2019). Effects of cell morphology and attachment to a surface on the hydrodynamic performance of unicellular choanoflagellates. J. Royal Soc. Interface, 16(150), 20180736. 
[3] Schuech, R., Cortez, R., & Fauci, L. (2022). Performance of a helical microswimmer traversing a discrete viscoelastic network with dynamic remodeling. Fluids, 7(8), 257.
[4] Wróbel, J.K., Cortez, R., & Fauci, L. (2014). Modeling viscoelastic networks in Stokes flow. Phys. Fluids, 26, 113102.