A Persistent Homology Approach to Characterize Honeybee Behavior During Food Exchange

Trophallaxis—the direct exchange of food among nestmates—is one of the most prominent instances of eusociality in insects. It is part of a critical division of labor for honeybees (Apis mellifera L.); forager honeybees gather food from distant sources and distribute it via regurgitation to workers that remain in the hive. This process enables the efficient dissemination of nutrients and is crucial to the colony’s growth and survival. Previous studies have provided valuable insights into this food distribution process, but a mechanistic understanding is still missing — how do these individual exchanges cause nutrients to flow across the colony?

We performed a series of experiments to systematically quantify trophallaxis and ultimately develop an agent-based model that can replicate it. To do so, we employed an experimental setup with a group of honeybees that had been deprived of food for 24 hours. After observing their behavior for several minutes, we introduced multiple "donor" bees that had retained free access to food until that point. Interesting patterns emerged in the collective behavior during the experiment’s different phases. The deprived bees initially moved around the experimental arena in a manner that appeared to be stochastic, but they formed clusters after the donors entered the area — presumably to exchange food. These clusters eventually dispersed, and the stochastic motion resumed in a pattern that we conjecture reflects the end of food distribution. Snapshots of these three behavioral phases appear in Figure 1.

Several questions arise from these observations. Can we systematically characterize the experiment’s three phases—pre-trophallaxis, trophallaxis, and post-trophallaxis—and estimate the time spent on food distribution within the group? How many clusters do the bees form, and what size are they? How long do these clusters last? Do the results change as a function of the number of bees or the fraction of donors?

To answer these queries, we recorded high-speed video of the experiment [3] and used image-processing techniques to separate bees from the background and produce a point-cloud representation of their positions. Researchers may study the cluster patterns in such a data set in many potential ways. For example, one can choose a scale parameter \(\epsilon\), connect all the points within a proximate Euclidean distance of \(\epsilon\), and calculate the properties of these \(\epsilon\)-connected components. While this approach is certainly useful for preliminary analysis, it also leads to challenges — notably, the choice of \(\epsilon\). Too small of an \(\epsilon\) means that most of the points remain isolated; if the value is too large, all of the points connect together into a single component. Neither option is very useful from the standpoint of our research questions.

Topological data analysis (TDA) [7]—an approach that characterizes the shape of real-world data—serves as an elegant solution to this problem. TDA varies the resolution parameter \(\epsilon\) that connects the points together, then determines the homology of the resulting complex in terms of its connected components \(\beta_0\), two-dimensional (2D) holes \(\beta_1\), three-dimensional voids \(\beta_2\), and so on. This approach has grown in popularity for a variety of applications over the past decade, including some biological aggregation problems [1, 4]. Since we are concerned with the clustering aspect of bees on a 2D plane, examining the connected components is sufficient. We produce a point-cloud data set from a single video frame and compute \(\beta_0\) for a range of \(\epsilon\) values. Figure 2a depicts the results of carrying out this procedure on a snapshot from the experiment. A vector of these counts—which one can visualize in several ways (persistence diagrams, barcodes, etc.)—captures the cluster structure in rich detail.

Since this is a dynamical systems problem with multiple behavioral regimes, we must also consider how we can effectively capture the homology’s evolution. Again, previous work has proposed a number of methods that accomplish this objective [2, 5, 6]. We used the CROCKER method (Contour Realization Of Computed \(k\)-dimensional hole Evolution in the Rips complex) [5], which is a contour-based visual representation of the \(\beta\) vector that captures the clustering behavior as a function of both \(\epsilon\) and time. CROCKER plots utilize color codes for the number of clusters that exist at each \(\epsilon\) value. For example, the dark red color in the upper regions (higher \(\epsilon\) values) of the \(\beta_0\) CROCKER plot in Figure 2b signifies that the complex contains between zero and three clusters; the blue contour that corresponds with lower \(\epsilon\) values represents 36-39 clusters. At any given time point on the horizontal axis, the \(\epsilon\) values at which each of these contours lie reveal the degree of clustering. For instance, consider “A” in Figure 2 — the complex constructed with \(\epsilon=100\) from the point cloud at \(t=200\). This complex contains ten clusters, a value that falls in the orange range of the colorbar to the right of the CROCKER plot. “B” in Figure 2 has \(\epsilon=250\), which leads to a value of \(\beta_0=4\) that is color coded in bright red; at \(\epsilon=600\)—as in “C” in Figure 2—all of the bees are in a single connected component (\(\beta_0=1\)) that corresponds to dark red.

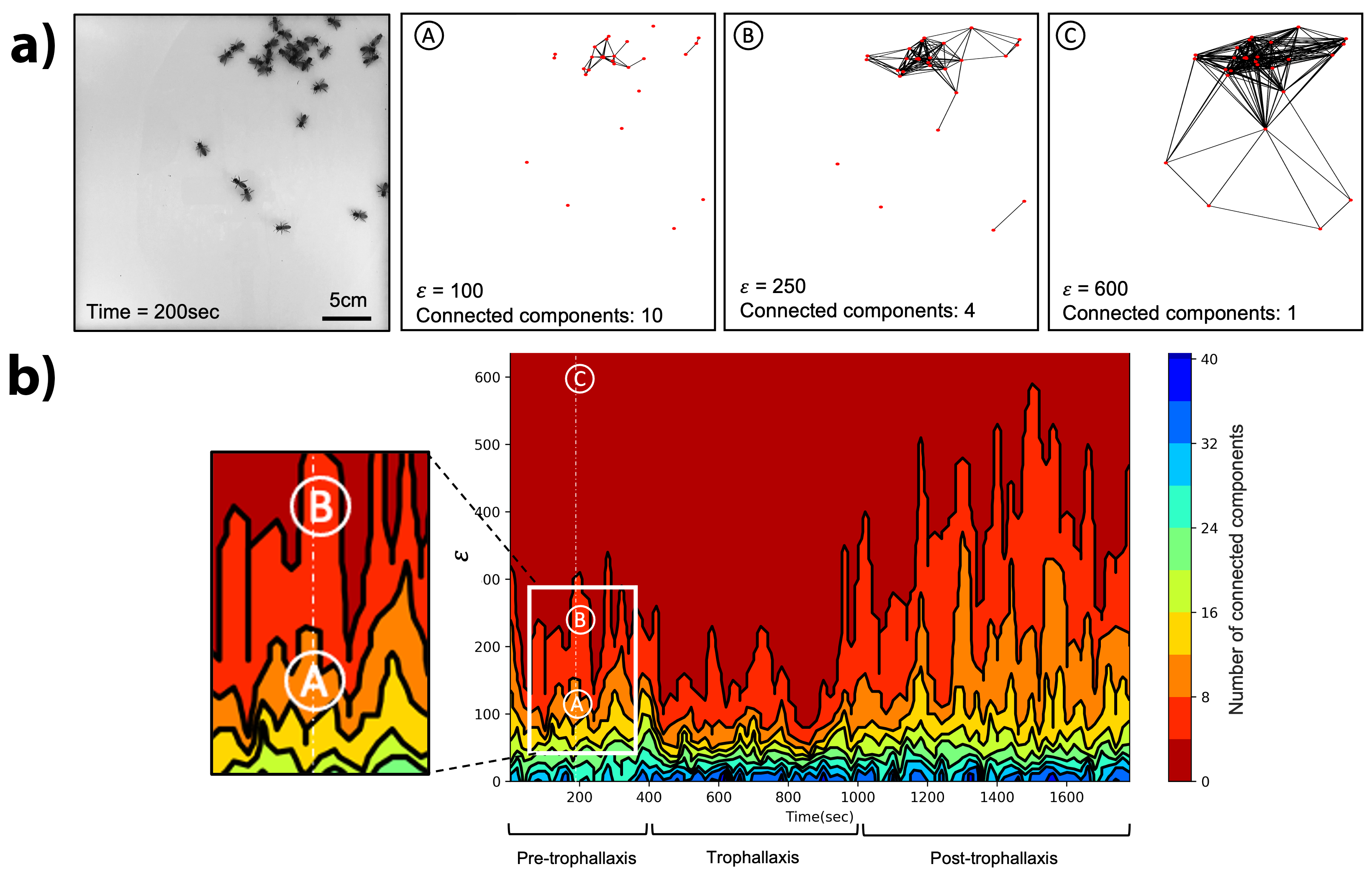
We can use the geometry of the various contours in such a plot to study how clustering changes over time and reveal regime shifts in the collective behavior of honeybees. For example, a quick visual inspection of the CROCKER plot in Figure 2 clearly reveals shifts in the patterns of the contours at \(t \approx 450\) and \(t \approx 1{,}000\) seconds. The first of these time points coincides with the introduction of donor bees into the experimental arena. The deprived bees were dispersed randomly before that time, so there are a large number of small clusters in the complex (the blue and green contours in Figure 2b) and not many large clusters; this result is reflected in the height of the contour that divides orange (four-eight clusters) from bright red (zero-four clusters). In other words, a higher value of \(\epsilon\) is necessary to capture all of the bees in a small number of clusters, which reflects their largely random spatial distribution.

During the middle phase of the experiment, the clustering that is visible in Figure 1b lowers the uppermost contour; since the bees are close to each other, a small \(\epsilon\) value connects them in a few big components. The light blue and green contours do not alter significantly during the time span of the experiment. These contours correspond to lower \(\epsilon\) values—i.e., the formation of clusters with one to two bees—and therefore change very little across the different clustering phases. Finally, we also notice that the dark blue contours, which correspond to the highest number of connected components on the colorbar, are only present during the trophallaxis and post-trophallaxis phase. This phenomenon is caused by the increased overall number of bees that follows the introduction of fed bees at the beginning of the trophallaxis phase. The maximum number of connected components (equal to the total number of bees) thus increases and introduces the dark blue contours.

Biologically, clustering is a natural product of trophallaxis because the bees must physically gather together to distribute food. We can therefore naturally label the period when a lot of clustering occurs as the trophallaxis phase. Following this reasoning, we conjecture that the second regime shift at \(t \approx 1{,}000\) happens once the food is mostly distributed across the group and no more exchanges are taking place. During this phase, the bees—who are no longer hungry—spread apart in the arena in a low clustering configuration that is similar to the first phase. While the first and third phases are both clustered relatively loosely when compared with the second, a clear distinction still exists between them. The clustering in the third phase is looser than in the first (as evidenced by the higher peaks in the uppermost contour of Figure 2b’s CROCKER plot). This result could stem from the underlying biological behavior; the bees have no reason to be close to each other after trophallaxis since they are not hungry.

Animation 1 presents the homology’s dynamics as captured by the CROCKER plot. The video illustrates how the clustering changes with time (as represented by the vertical dark line on the CROCKER plot). We see how the clustering varies with increasing \(\epsilon\) values at \(t \approx 120\) (as represented by the horizontal white line and the white dot at its intersection with the dark line). The corresponding experimental data frame that was captured at the time stamp equal to the \(x\) coordinate of the dark line is displayed below the CROCKER plot. At \(t \approx 120\), we show the overlay of the point cloud data and the changing Rips complex as a function of epsilon (\(\epsilon\)), equal to the \(y\) coordinate of the white line.

We can automatically detect these regime shifts by applying a changepoint detection approach to the first principal component of the CROCKER matrix, thereby formalizing the aforementioned reasoning. We have successfully replicated all of these analyses for multiple runs across different densities and numbers of bees, which confirms that CROCKER plots are useful representations for the quantification of regime shifts that occur during trophallaxis. There are a number of applications for this approach, beginning with a formal assessment of the effects of different parameters—such as the time spent on food distribution, the average number of clusters, and the average cluster size during trophallaxis—on trophallaxis observations. TDA results captured in CROCKER plots can also help us calibrate and validate models of this interesting and important behavior; this outcome could ultimately yield insights about the decision-making process at the individual level that leads to global food management at the colony level.

Elizabeth Bradley presented this research during a minisymposium at the 2021 SIAM Conference on Applications of Dynamical Systems, which took place virtually in May 2021.

References

[1] Amézquita, E.J., Quigley, M.Y., Ophelders, T., Munch, E., & Chitwood, D.H. (2020). The shape of things to come: Topological data analysis and biology, from molecules to organisms. Dev. Dyn., 249(7), 816-833.
[2] Cohen-Steiner, D., Edelsbrunner, H., & Morozov, D. (2006). Vines and vineyards by updating persistence in linear time. In Proceedings of the twenty-second annual symposium on computational geometry (pp. 119-126). New York, NY. Association for Computing Machinery.
[3] Fard, G.G., Bradley, E., & Peleg, O. (2020). Data-driven modeling of resource distribution in honeybee swarms. In ALIFE 2020: The 2020 conference on artificial life (pp. 324-332). International Society for Artificial Life.
[4] McGuirl, M.R., Volkening, A., & Sandstede, B. (2020). Topological data analysis of zebrafish patterns. PNAS, 117(10), 5113-5124.
[5] Topaz, C.M., Ziegelmeier, L., & Halverson, T. (2015). Topological data analysis of biological aggregation models. PloS One, 10(5), e0126383.
[6] Xian, L., Adams, H., Topaz, C.M., & Ziegelmeier, L. (2020). Capturing dynamics of time-varying data via topology. Preprint, arXiv:2010.05780.
[7] Zomorodian, A., & Carlsson, G. (2005). Computing persistent homology. Discrete Comput. Geom., 33(2), 249-274.