A Pressure Puzzle: More is Less

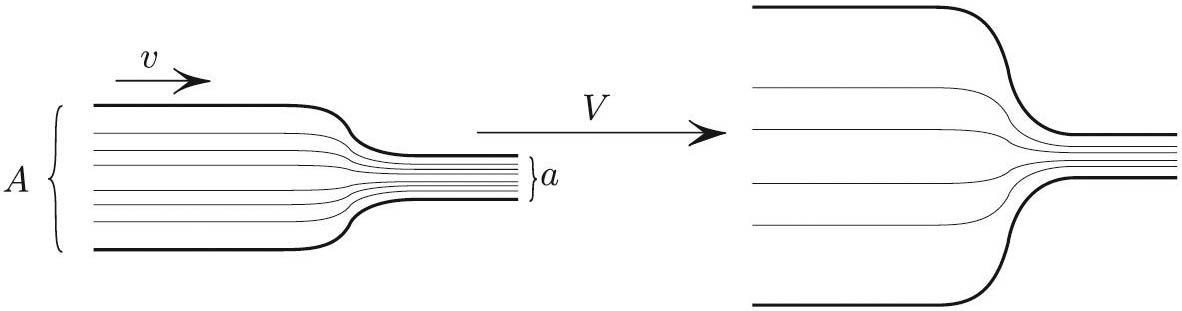
Water—treated here as an ideal fluid—flows steadily through a pipe with a narrowing, driven by excess pressure \(p\) in the wider portion. Wishing to increase the flow rate, I widen the wider portion even more (see Figure 1) while maintaining the same excess pressure \(p\) as before. Will this widening achieve the desired result and increase the flow rate? Readers may wish to pause here before reading on.

The answer is the opposite of what one might expect: the flow rate will actually decrease. But how can widening any part of the pipe decrease the flow rate? The resolution of this paradox is that I “forgot” that the driving pressure remains fixed. In an extreme case where the pipe barely narrows, one must push water very quickly to sustain the pressure differential. Therefore, narrowing the wide part increases the flow. In other words, a disparity in thickness increases the resistance because a greater disparity in thickness means a greater change of speed when the water enters a narrower section — and this requires more effort.

Here is a formal proof. By Bernoulli’s law,

\[\require{cancel} \frac{\rho v ^2 }{2} + p+\cancel{p_{\rm atm }}= \frac{\rho V ^2 }{2}+\cancel{p_{\rm atm }},\tag1\]

where \(p\) is the driving pressure and \(v\), \(V\) are the velocities, as marked in Figure 1. Since the water is incompressible, the volumes that enter and leave per second are equal:

\[Av = aV,\]

where \(A\), \(a\) are the cross-sectional areas (larger quantities are denoted by capitals). Substituting \(v= \frac{a}{A} V\) into \((1)\) and solving for \(V\) gives

\[V ^2 = \frac{2p/ \rho }{1- \bigl( \frac{a}{A} \bigl) ^2}.\tag2\]

Fixing the exit cross-section \(a\) and letting \(A\downarrow a\) yields \(V \rightarrow \infty\), and so the flux \(aV \rightarrow \infty\); this confirms the aforementioned intuitive conclusion. Maintaining a fixed \(p\) when \(A\approx a\) requires huge flux.

At the other extreme, widening the supply pipe \((A \rightarrow \infty)\) while still fixing the exit \(a\) leads to a saturation limit for the flux \(aV\), since \(a\) is fixed and

\[V ^2 \rightarrow 2p/ \rho,\tag3\]

according to \((2)\). 

What does all of this have to do with the well-known fact that water shoots out of a hole in the side of a barrel with velocity \(V\) depending only on the depth of the hole: \(V= \sqrt{ 2gh}\), where \(h\) is the depth? One can think of a hole in the barrel as a narrowing in a pipe where the driving pressure is hydrostatic, generated by the water column above the level of the hole and given by \(p = \rho g h\).

According to \((3)\), \(V= \sqrt{  2p/ \rho}\); substituting \(p = \rho g h\) indeed yields \(V= \sqrt{  2 g h }\). Incidentally, this is precisely the velocity that a free-falling drop (released from rest) would gain after distance \(h\). The idea of the previous sentence provides an alternative and immediate derivation of \(V = \sqrt{  2gh }\) for the velocity of the water that is shooting out of the hole in the barrel.