A Spin on Some Simple Geometry

Most middle schoolers probably know that rotating a rigid triangle does not change its area — a fact that is perhaps not mentioned because it seems so obvious and useless. High schoolers learn the Pythagorean theorem (at least, I hope they do) but are not told that the theorem is a consequence of the area’s invariance.

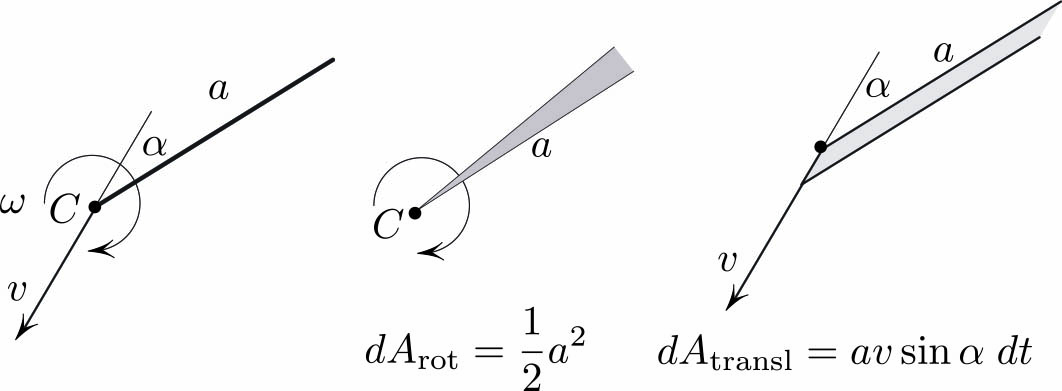
Before we start rotating triangles and causing their sides to move, we need the simple observation in Figure 1: a moving segment of constant length sweeps the area at the rate

\[\underbrace{\frac{1}{2} \omega a ^2}_{\textrm{rotation}}  + \underbrace{v a \sin  \alpha}_{\textrm{translation}}.\tag1\]

The Theorem of Cosines

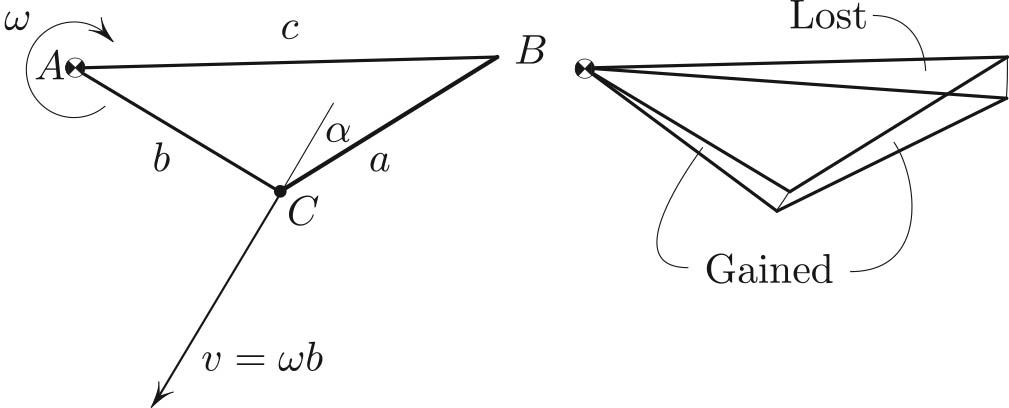
The theorem of cosines amounts to the statement \(\frac{d}{dt} \textrm {area}=0 \) when the triangle rotates on its vertex.¹ Rotating clockwise as in Figure 2, the area is gained by two of the sides and lost by side \(AB\). For the sides \(AC\) and \(AB\) that rotate clockwise with \(\omega =1\), the rates are \(\frac{1}{2} a ^2\) and \(-\frac{1}{2} c ^2\). For the remaining side \(BC\), we substitute \(v = \omega b =b\) into \((1)\) and note that \(\sin  \alpha = \sin  (\angle C-  \pi /2)=\) \(-  \cos \angle C\) in Figure 2. Therefore, \(CB\) sweeps the area at the rate

\[\frac{1}{2} a ^2 + b a \sin  \alpha = \frac{1}{2} a ^2 - ba \cos C. \]

To summarize, the rate of change of the area of \(\Delta ABC\) is

\[\underbrace{\frac{1}{2} b ^2 }_{ AC} + \underbrace{\frac{1}{2} a ^2 - ba \cos C }_{ CB} - \underbrace{\frac{1}{2} c ^2 }_{ BA }=0, \tag2\]

where each underbrace represents the rate at which the area is swept by the corresponding side. We obtained the theorem of cosines:

\[c ^2 = a ^2 + b ^2 - 2ab \cos C.\tag3\]

Each underbraced term in \((2)\) has a meaning that is lost in \((3)\), but I still prefer the beauty of \((3)\) — a shallow attitude, perhaps.

Milking the Invariance 

By rotating the triangle around other points, we can (re)discover some identities. Here are two examples.

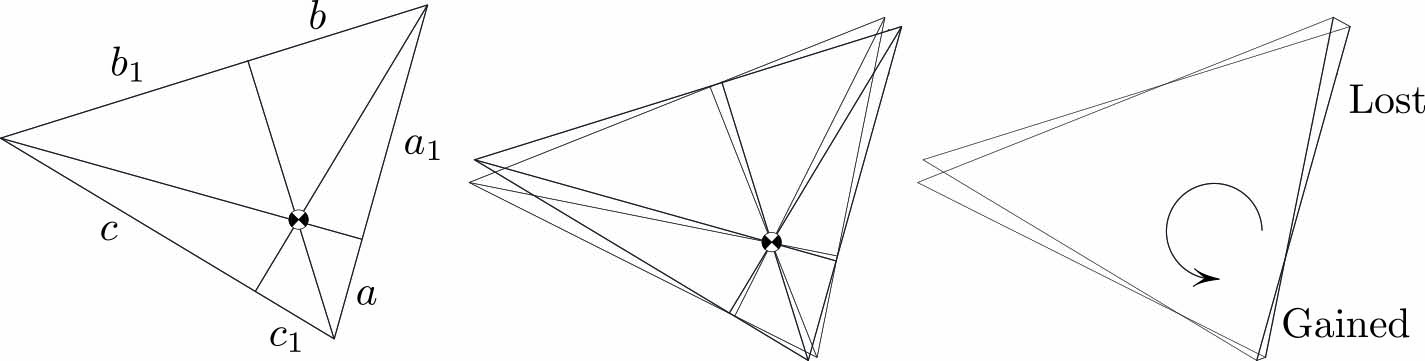
Example 1. When rotating about the orthocenter, Figure 3 gives

\[ a^2 + b ^2 + c ^2 = a_1 ^2 + b_1 ^2 + c_1 ^2.\tag4\]

The left side of the formula represents the rate at which the area is acquired, and the right side represents the rate of loss; equality amounts to the area’s constancy. A quick alternative proof of \((4)\) goes by application of the Pythagorean theorem, but this is of course not the point.

Example 2. Let us now rotate the triangle around its centroid, i.e., the point of intersection of the medians (see Figure 4). The constancy of the area translates to

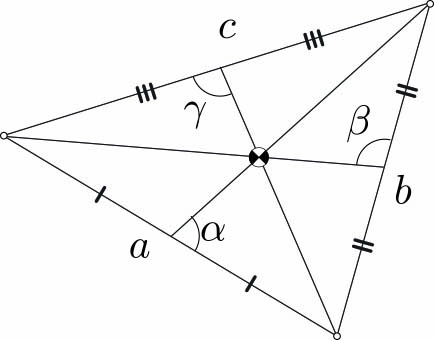
\[a\, m_a \cos \alpha + b\,m_b \cos \beta + c\,m_c \cos \gamma = 0,\tag5\]

where \(m_a\), \(m_b\), and \(m_c\) are the lengths of the medians. To justify \((5)\), we note that the midpoint of side \(a\) moves with speed (keeping \(\omega =1\))

\[m_a/3,\]

at the right angle to the median. Furthermore, rotation of the side around the midpoint contributes nothing to the change of area. The side thus sweeps the area at the rate

\[\frac{1}{3} m_a  a \sin \biggl( \frac{ \pi }{2} - \alpha \biggl) =\frac{1}{3} m_a  a\cos \alpha;\]

adding the rates for all three sides yields \((5)\).

One can further milk the area (or volume) invariance for other figures (or solids in \(\mathbb{R}^3\)).

¹ We think of the time as the angle of rotation, thus making the angular velocity \(\omega =1\).

The figures in this article were provided by the author.