A Western Sunrise
In a distant galaxy, a lone planet orbits its sun; all other celestial bodies are far away. The planet’s axis is not tilted relative to the ecliptic (the plane of its orbit).
For many days, a creature living on the planet’s equator has been watching the sun rise in the east and set in the west. One evening, the sun sunk as usual below the western ocean and the light began to fade — but then it stopped fading, the sky brightened, and the sun rose back up from where it just set, from the west! The sun then described the arc overhead and set in the east. After a brief period of darkness, the sun reappeared in the east, made its overhead arc, and set in the west — just as in previous days. How did this happen?
A Solution
Let us first consider the planet with zero axial spin. To the creature on such a planet, the sun will travel east—as in Figure 1—and make one revolution in the sky per year. For eccentric orbits, this eastward progression is very uneven: fast for a short time and slow most of the time. This spike occurs when the angular velocity \(\omega_{\rm orbital}\) of the planet’s position vector relative to the sun spikes during the close passage to the sun, near the perihelion. The key to the puzzle’s solution is that during the quick passage between points \(A\) and \(B\) in Figure 1, the sun travels by more than \(180 ^\circ\) in the sky — and does so rapidly.
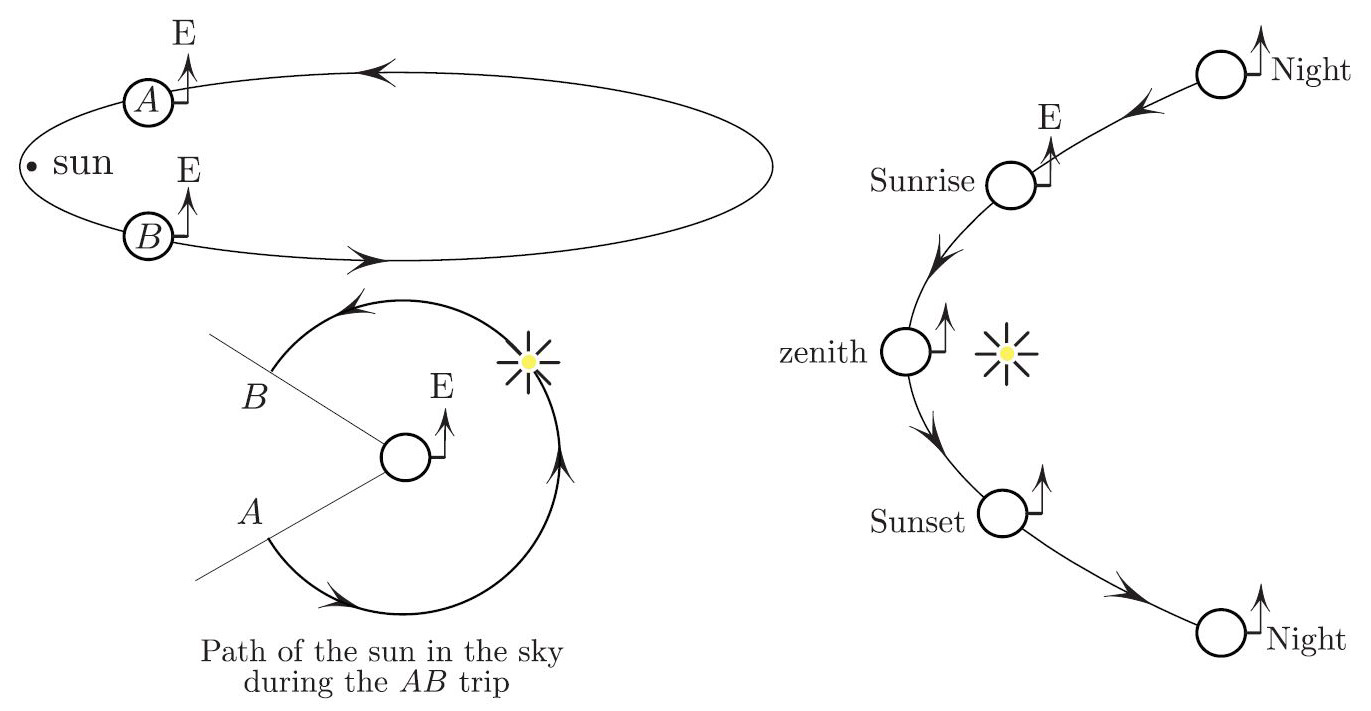
Let us now spin our planet on its axis with angular velocity \(\omega_{\rm spin}\) in the same direction as travel around the sun, i.e., counterclockwise in Figure 1, just like Earth. The sun—as seen in the sky—will thus acquire angular velocity \(\omega_{\rm spin}\) east to west (the conventional direction), in addition to the preexisting \(\omega_{\rm annual}\) in the opposite direction. In the planet’s sky, the sun will therefore travel with angular velocity
\[\omega_{\rm sun} = \omega _{\rm spin}- \omega_{\rm orbital},\tag1\]
measured from east to west. With a sufficiently eccentric orbit (see Figure 1), \(\omega_{\rm orbital}\) experiences a spike that can dominate \(\omega _{\rm spin}\) and makes \(\omega_{\rm sun}\) change sign. This occurrence manifests as the reversal of the sun’s motion in the sky. With sufficient eccentricity, the sun’s backward travel by \(> 180^\circ\) for the spinless planet happens so quickly that the spin does not appreciably change this angle. It is thus possible for the sun to make a west-to-east trip in the sky by more than \(180^\circ\) once a year.
Back to Earth
For those of us on Earth, \(\omega _{\rm spin} >> \omega_{\rm orbital}\) so that \(\omega _{\rm sun}\) does not change sign — although it does vary. A very slight slowdown of the sun’s travel from east to west occurs as we get closer to the sun. This year we passed the perihelion on January 2; the sun advanced the slowest in our sky around that day, but of course not slow enough to move backwards.
Sliding Days
Another interesting consequence of the eccentricity of Earth’s orbit is the “sliding” of the daylight time for a few days around each solstice. For example, at \(40^\circ\) latitude—roughly the latitude of State College, Pa.—there is a period of about three weeks around December 21 when both sunrise and sunset occur later and later with each passing day. The daylight interval slides from day to day and becomes the shortest on December 21, after which it continues sliding while also elongating. Around January 4 or so, the sunrise times reverse and begin getting earlier with each passing day.
On Focus
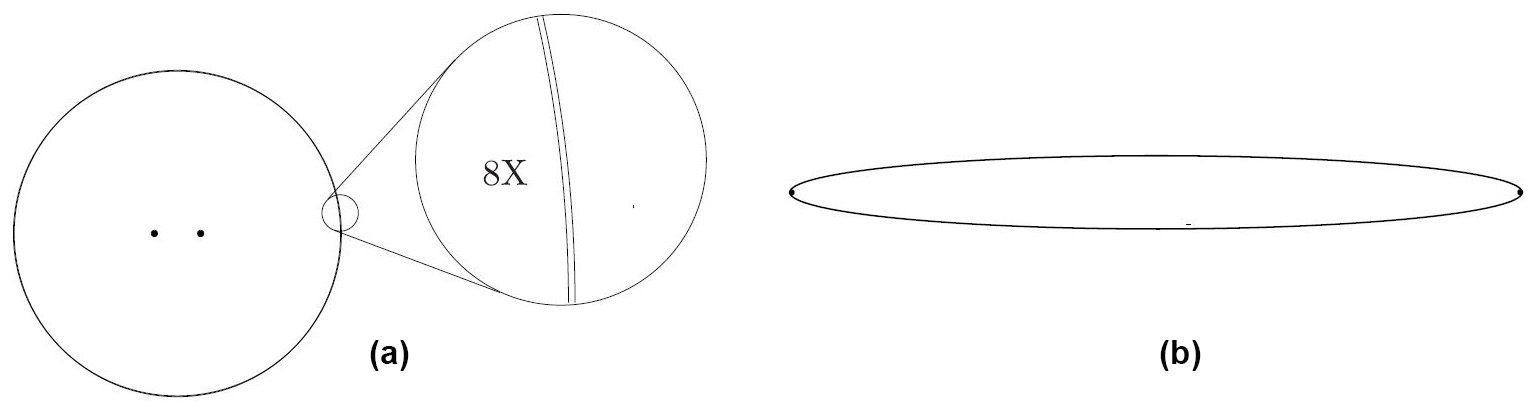
It is interesting to note the close proximity of the foci of an elongated ellipse to the vertices of the ellipse, i.e., the closeness of the planet as it passes by the sun. Figure 1 illustrates this phenomenon with anatomical correctness: the semiaxes \(a=1\) and \(b= 0.25\) and the distance in question is \(< 0.032\) (this distance is \(a-c\), with \(c = \sqrt{ a ^2 - b^2 }\) as the distance from the focus to origin). The focus is over 96 percent of the way from the center of the ellipse to its vertex. For the \(1:10\) aspect ratio, the foci seem to almost lie on the ellipse in the resolution of Figure 2.
As a flip side of this coin, consider a nearly round ellipse. The distance between the foci for such an ellipse is large relative to \(a-b\): it is \(2 \sqrt{ a ^2 - b ^2 } = 2\sqrt{ (a+b)(a-b) } > 2\sqrt{ 2b } \sqrt{ (a-b)}\). Figure 2 illustrates the way in which a tiny deformation causes a relatively great split of the center into foci. A circular room serves as a good whispering gallery if the speaker and listener are symmetrically positioned relatively close to the center, as in Figure 2. This is so because the circle is almost indistinguishable from an ellipse with these foci.1
The figures in this article were provided by the author.
1The ellipse is in fact close to the circle in the \(C^2\)-norm, which is what matters for the focusing properties.
About the Author
Mark Levi
Professor, Pennsylvania State University
Mark Levi (levi@math.psu.edu) is a professor of mathematics at the Pennsylvania State University.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



