Active Hydraulics as Analog Computers to Solve Complex Problems

Mathematical models for complicated physical systems rarely have exact solutions. In turn, models that do have exact solutions often fail to quantitatively describe real-world phenomena, though they may sometimes provide qualitative insights that facilitate the construction of more realistic theories.

Now, a new set of active matter experiments have matched an exact solution for a particular system known as the six-vertex or ice-type model. Researchers previously used this model—which dates back to the 1930s and was solved in the 1960s—in a wide range of applications, none of which explicitly matched the precise solution to the equations. However, physicists Camille Jorge and Denis Bartolo of the University of Lyon in France recently found that tiny beads in a square grid of tubes behave specifically and quantitatively as predicted by the six-vertex model’s solution [3].

Unlike typical physics models where particles only act under external forces, an active matter framework allows the basic agents to move on their own. For this reason, active matter research has found applications in flocking animals [2], tangling proteins, and nonequilibrium systems for which Newtonian physics descriptions are too unwieldy.

Bartolo and his collaborators developed a form of active matter that they call active hydraulics: plastic particles that move at a constant velocity without being driven by fluid pressure. The direction of motion is entirely determined by local conditions, which are themselves set by surrounding particles in the fluid. The particles collectively and spontaneously form currents inside tubes based on the tubes’ configurations, which prompts the active hydraulic system to “solve” the six-vertex model within tubes that form a square lattice.

This finding has important implications for the description and control of other active matter systems, including organisms like bacteria, artificial particles for drug delivery, and microrobotics. It also serves as a strong demonstration of active matter’s usefulness as a kind of analog computer. The creation of different lattice configurations or introduction of biases in particle motion could potentially simulate many types of systems in statistical physics, materials science, and mathematical biology — ultimately providing a set of tools beyond computer models for complex systems.

“We didn’t intend to look at the six-vertex model,” Jorge said, noting that the experiment offers hints about how to reverse engineer solutions for more sophisticated models. “Maybe it’s a new, easier way to do physics — not starting from the very fundamental basics of physics, but just trying to have a broad description that captures the essence of the phenomenon.”

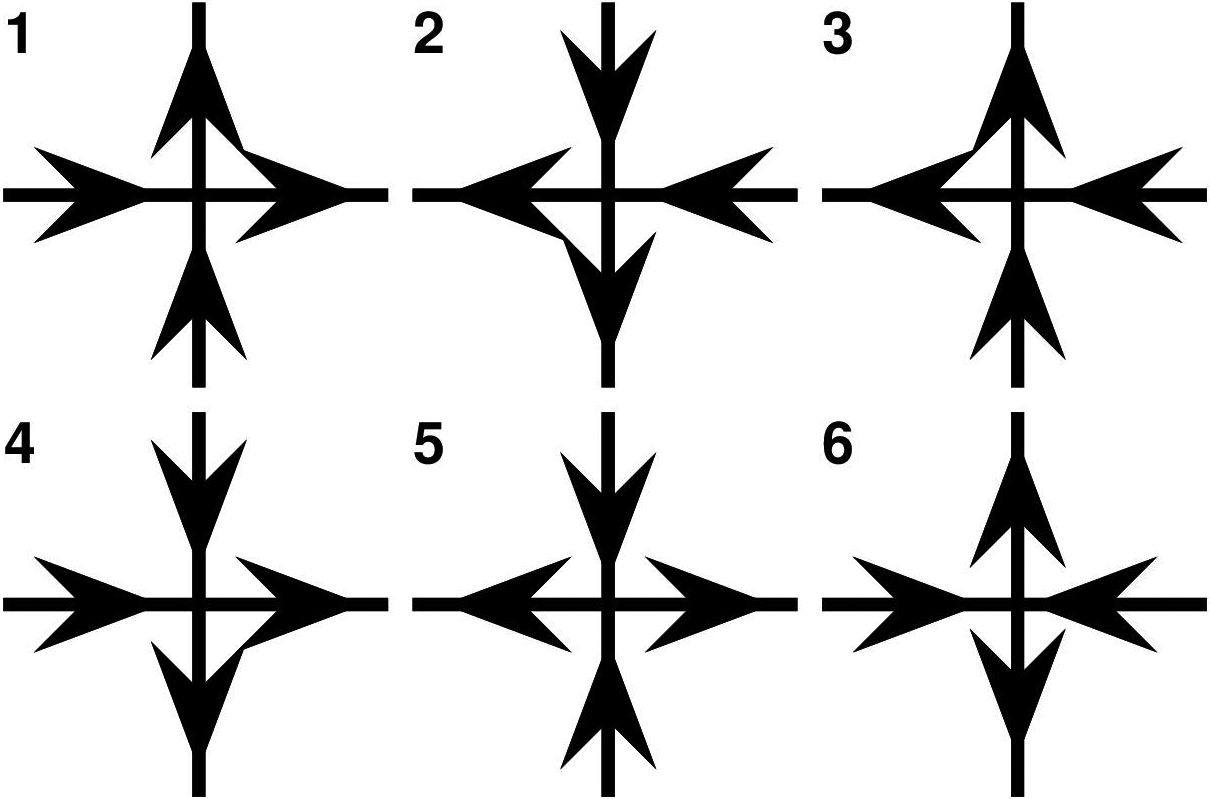
The Six-vertex Model

The six-vertex model is based on Nobel Prize-winning chemist Linus Pauling’s attempts to understand the structure of water ice [5]. By the 1930s, experiments revealed that the oxygen atoms in ice form a variety of tetrahedral structures, with hexagonal rings of molecules in two of the dimensions.¹ However, the crystallographic methods of the time were unable to determine the positioning of the hydrogen atoms. Pauling realized that he could model the structure by linking each oxygen atom with four hydrogen atoms: two with tight molecular bonds to create H₂O, and two with looser hydrogen bonds to assemble the entire crystal structure. He speculated that doing so would explain some of ice’s stranger properties.

Although this six-vertex model did not actually explain ice particularly well on a quantitative level, flattening the three-dimensional lattice to form a system of square cells (like graph paper) yielded a mathematical description with an exact solution. In this model, each intersection in the lattice has two arrows that point towards the intersection and two that point outwards — leading to six possible configurations (see Figure 1). As an aside, the arrows in Pauling’s original version pointed from the oxygen atom towards the hydrogen atom in a neighboring H₂O molecule.

The system is described by its partition function

\[Z=\sum_k \textrm{exp}(-E_k/k_B T),\]

where \(k_B\) is the Boltzmann constant, \(T\) is temperature, and

\[E_k=\sum^6_{i=1} n_{i,k}\epsilon_i\]

is the energy for each possible configuration. Here, \(n_{i,k}\) is the number of vertices in the lattice and \(\epsilon_i\) is the energy of each vertex type. One can set the energy of each state for ice itself equal to zero, so \(Z\) simply tallies all of the possible configurations in the lattice. The antiferroelectric state—which exhibits a local electric field even in the absence of an external field, with electric polarization alternating between adjacent sites in a lattice—is denoted by

\[\epsilon_1=\epsilon_2=\epsilon_3=\epsilon_4>0 \quad \textrm{and} \quad \epsilon_5=\epsilon_6=0,\]

such that vertex types \(5\) and \(6\) are preferred energetically. The six-vertex model can thus describe the phase transition between a disordered state and an antiferroelectric state, among other systems.

Spinning Fluids Got to Go ‘Round

On the experimental side, Bartolo’s laboratory previously developed a type of active matter that was meant to resolve a common problem in these systems. For most varieties of active matter, self-organization often arises via collisions or other local interactions that are difficult to model, leaving only macroscopic heuristic descriptions. The researchers surmounted this difficulty by exploiting an obscure electromagnetic effect that was originally described by Georg Hermann Quincke in the 19th century.

Quincke discovered that nonconducting spheres (e.g., made of glass or plastic) rotate at a fixed rate in a uniform electric field. As such, Bartolo and his colleagues placed tiny Plexiglas beads—which they dubbed “Quincke rollers”—between horizontal glass plates and applied a vertical electric field, which caused the beads to roll along the bottom plate at a constant velocity but in a random direction [1]. “In a straight pipe, the liquid has to flow because of the activity,” Jorge said. “It’s a spontaneous symmetry breaking. The liquid can flow from the left to the right or the right to the left without applying any pressure.”

With these initial results in hand, Jorge and Bartolo built a square lattice of pipes. For ordinary fluids, it would be impossible to maintain a steady velocity through any part of this configuration. However, the spontaneous motion of the Quincke rollers allowed the researchers to execute an entirely new class of experiments with several profound results.

“When we [performed] the experiment, we had a constant magnitude of the current,” Jorge said. The current maintained the same magnitude of \(J_0 \approx 1,300\) particles/second in each segment of the lattice — an effective quantization of the fluid motion that can be represented mathematically as a spin. “When we put all these spins on a map, we had two arrows in and two out at each node of the network,” Jorge continued. “We immediately recognized the six-vertex model from our physics background.”

The flow of the active hydraulic particles was steady but did not have a defined order. However, the team found that the six vertex types are not equally likely to appear, even though they are all energetically equivalent; types \(5\) and \(6\) (where currents flow head-to-head into a junction) were roughly half as likely to occur as the configurations where currents flow through the junction in a straight line.² Placing cylindrical posts in the centers of the junctions enabled the experimenters to change the system’s effective energy configuration. They induced a phase transition as a function of the post radius; at larger radii, the 5th and 6th junction types came to dominate the others, simulating a phase transition that is evident in six-junction models for antiferroelectric materials (see Figure 2).

In this completely ordered phase, the current only flows in closed loops, forming a self-similar pattern across scales — that is, a fractal. All of these results exactly match the six-vertex model’s predictions, which no other experiments have replicated as precisely. The implications are noteworthy.

Four Rules for Active Hydraulics

Because the square lattice is a simple configuration, the six-vertex model and related models are able to exhibit exact solutions. Jorge, Bartolo, and their colleagues have already investigated the use of active hydraulics on more complex two-dimensional geometries [4], but the main value of these experiments stems from the resulting general principles.

For instance, a hexagonal (honeycomb) lattice consists of three—rather than four—pipes that are attached to each vertex. To satisfy mass conservation under a steady flow, some segments have no net current (any local motion averages to zero across the whole segment), thus creating more complicated configurations than in the square lattice instance. Even more elaborate behavior arises in triangular lattices, for instance, where six pipes enter each vertex.

Jorge and Bartolo identified four rules to help scientists understand active hydraulics in more complicated geometries.

1. Mass is conserved so that all of the current that flows into a junction will flow out again: \(\sum J_k=0.\)
2. The current is quantized, which means that it can be represented as \(0\), \(+J_0\), or \(-J_0\) depending on the direction at which it flows into a junction.
3. The system’s phase is defined by the relative weight of each junction diagram, as in the six-vertex model.
4. If more than four pipes meet at a vertex, the geometry of the junction shapes the possible current configurations. For instance, a 32-vertex model—which offers many possible ways for the active fluid to enter and leave each junction, as well as zero-current segments—describes the triangular lattice.

In principle, these rules should apply to any lattice system. Since only a few models of this type have exact mathematical solutions, similar experiments could potentially provide a new technique for “calculating” solutions that would otherwise require approximate or numerical methods.

¹ This is technically known as a “wurtzite” (vurt-zite) configuration, though so much space is present inside the crystal structure of ice that the solid form of water is less dense than the liquid form. Most other materials are denser when solid.

² In other words, each of the first four junction types occur about 20 percent of the time, while the remaining two occur only 10 percent of the time.

References
[1] Bricard, A., Caussin, J.-B., Desreumaux, N., Dauchot, O., & Bartolo, D. (2013). Emergence of macroscopic directed motion in populations of motile colloids. Nature, 503(7474), 95-98. 
[2] Francis, M.R. (2023, November 1). Wildebeest self-organization via active matter theory. SIAM News, 56(9), p. 12.
[3] Jorge, C., & Bartolo, D. (2025). Active-hydraulic flows solve the six-vertex model (and vice versa). Phys. Rev. Lett., 134(18), 188302.
[4] Jorge, C., Chardac, A., Poncet, A., & Bartolo, D. (2024). Active hydraulics laws from frustration principles. Nat. Phys., 20(2), 303-309.
[5] Pauling, L. (1935). The structure and entropy of ice and of other crystals with some randomness of atomic arrangement. J. Am. Chem. Soc., 57(12), 2680-2684.