An Incompetence Problem

When ruminating recently on the question of finding a person who one can trust to do a job well (speaking of many occupations that range from lawyers and politicians to teachers, plumbers, and physicians), I thought of the following toy problem with no implied connection to reality.

Consider an occupation in which each member is classified as either “competent” or “incompetent” (this idealized binary division excludes gray areas). An incompetent person knows no better and thinks that everyone is competent. On the other hand, a competent individual correctly estimates the proportion \(p\) of competents. With the entire population assembled in a conference hall, everybody is asked to drop money in an urn according to their estimates of the percentage of competents in the room. An incompetent thus contributes 1 dollar while a competent contributes \(p\leq 1\) dollars, where \(p\) is the actual proportion of competents (let us treat \(p\) as a continuous variable). Once everyone has chipped in, we find that the average contributed amount is \(q\) dollars, where \(q\in(0,1]\) (note that \(q=0\) is impossible as a consequence of the rules).

The question is as follows: Can we recover the actual proportion \(p\) of competents from the knowledge of \(q\)? In other words, can we filter out the polluting contribution of the incompetents? 

Let us first find the competents’ total contribution. With \(N\) people in the room, \(Np\) of them are competent, each contributing \(p\) for the total contribution of \((Np)p= N p ^2\). And there are \(N(1-p)\) incompetents, each contributing 1 dollar for the total contribution of \(N(1-p)\). To summarize,

\[\underbrace{ \hbox{total collected} }_{N  q}=  \underbrace{  \hbox{by competents}}_{N p^2 } + \underbrace{ \hbox{by incompetents}}_{N(1-p)},\]

or

\[q= p ^2 -p +1 = \biggl( p-\frac{1}{2} \biggl)  ^2 + \frac{3}{4}.\tag1\]

From \((1)\), we recover two possible values:

\[p = \frac{1}{2} \pm \sqrt {q - \frac{3}{4}};\]

these are equidistant from the 50 percent mark (see Figure 1). We can think of \(q\) as an estimated probability of competence as measured by the imperfect process tainted by the “votes” of the incompetents. Here are a few observations.

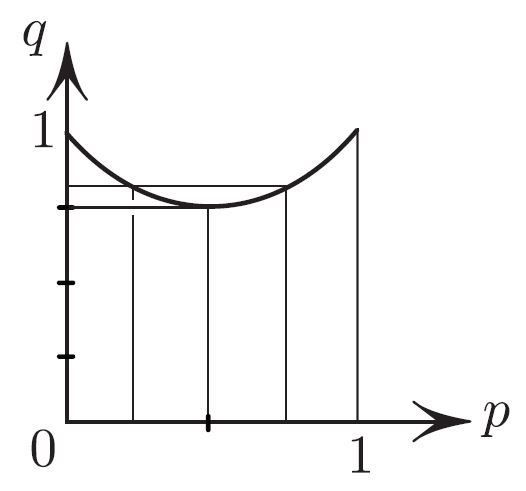
1. \(q\geq 3/4\) always, regardless of the split. 
2. The minimal \(q= 3/4\) occurs when the split is even \((p=1/2)\). One half (the competents) contributes \(1/2\) dollar each and members of the incompetent half each chip in \(1\) dollar; the average contribution is thus \(q=3/4\) dollars. Figure 1 reflects this conclusion.
3. \(p\) is determined uniquely only when \(q\) is least possible: \(q= 3/4\).
4. The good-sounding \(q=1\) is not necessarily good; it could also occur due to \(p=0\), where everyone is incompetent and thinks that they and all of their colleagues are great.
5. \(q>p\) for all values of \(p<1\). This is apparent from \((1)\) or the fact that incompetents contribute the maximum possible amount, thus raising \(q\) above \(p\).

After carrying out this thought experiment with no input from reality, I became curious and went online. A cursory search on lawyers yielded estimates of \(p=0.5\) from 1981 [1] and \(p=0.3\) from 2015 [2]. Of course, there is so much ambiguity in these estimates that making conclusions about trends—which do not look good at face value—would be a sign of incompetence itself. Yet regardless of the finer points, the estimate \(p\leq 1/2\) is certainly not comforting.

References

[1] Cramton, R.C. (1981). Lawyer competence and the law schools. Univer. Arkansas at Little Rock Law Rev., 4(1). Retrieved from https://lawrepository.ualr.edu/cgi/viewcontent.cgi?referer=https://www.google.com/&httpsredir=1&article=1418&context=lawreview.
[2] Tung, J.R. (2015). There’s a 70 percent chance you’re incompetent, survey suggests. FindLaw. Retrieved from https://blogs.findlaw.com/strategist/2015/10/theres-a-70-percent-chance-youre-incompetent-in-your-law-practice-survey-suggests.html.