Volume 56 Issue 06 July/August 2023
Research

Astroids Under Water

By

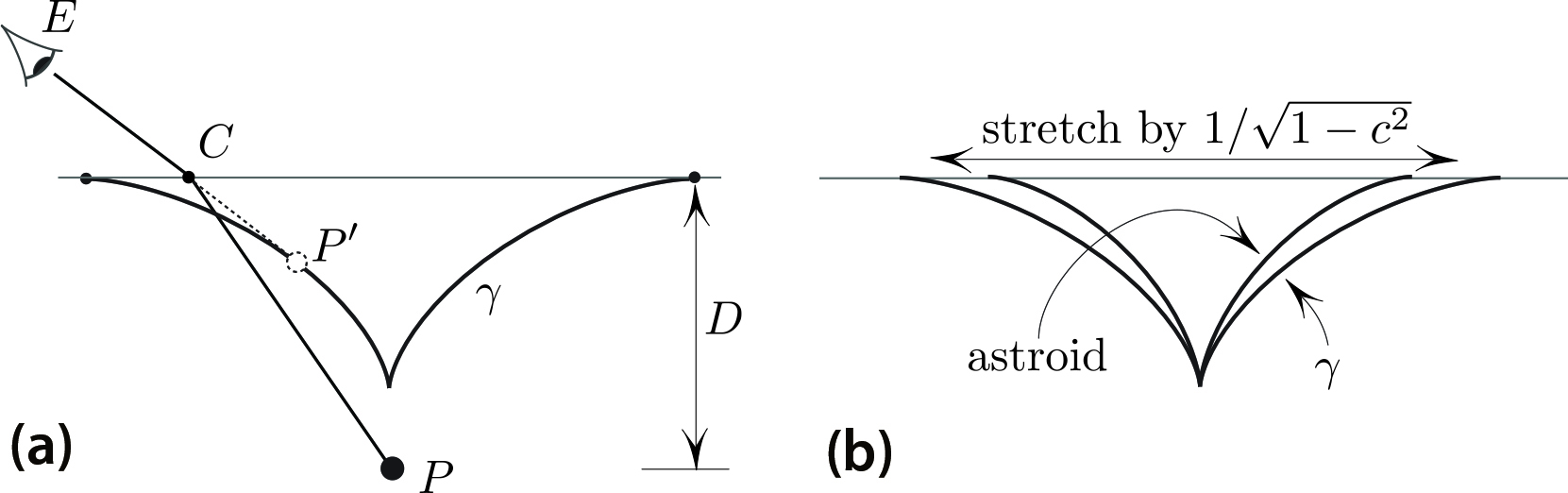
The observer in Figure 1 is looking at a pebble at the bottom of a clear lake. As the eye \(E\) moves, so does the pebble’s image \(P ^\prime\). The image \(O ^\prime\) stays on one special cusped curve \(\gamma\) wherever \(E\) is above water. This \(\gamma\) is the envelope of refracted rays that are emitted by the pebble. After writing about this curve in my May SIAM News article (“Some Shallow Observations”), I discovered—via a slightly boring calculation—that this curve is obtained by stretching astroid \[x^{2/3}+ y^{2/3}= a^{2/3}\tag1\] in the \(x\)-direction by the factor \(1/\sqrt{1-c^2}\), where \(c=v_{\rm {water}}/v_{\rm {air}}\approx 0.7\) is the speed of light in the water relative to that in the air and \[a=Dc,\] where \(D\) is the depth of the pebble.

<strong>Figure 1.</strong> The set \(\gamma\) of images of the pebble <strong>(1a)</strong> is the stretched astroid <strong>(1b)</strong>.
Figure 1. The set \(\gamma\) of images of the pebble (1a) is the stretched astroid (1b).

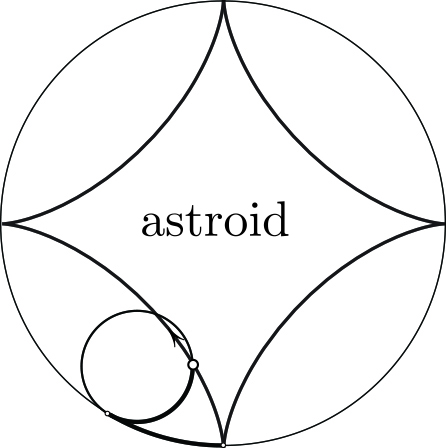
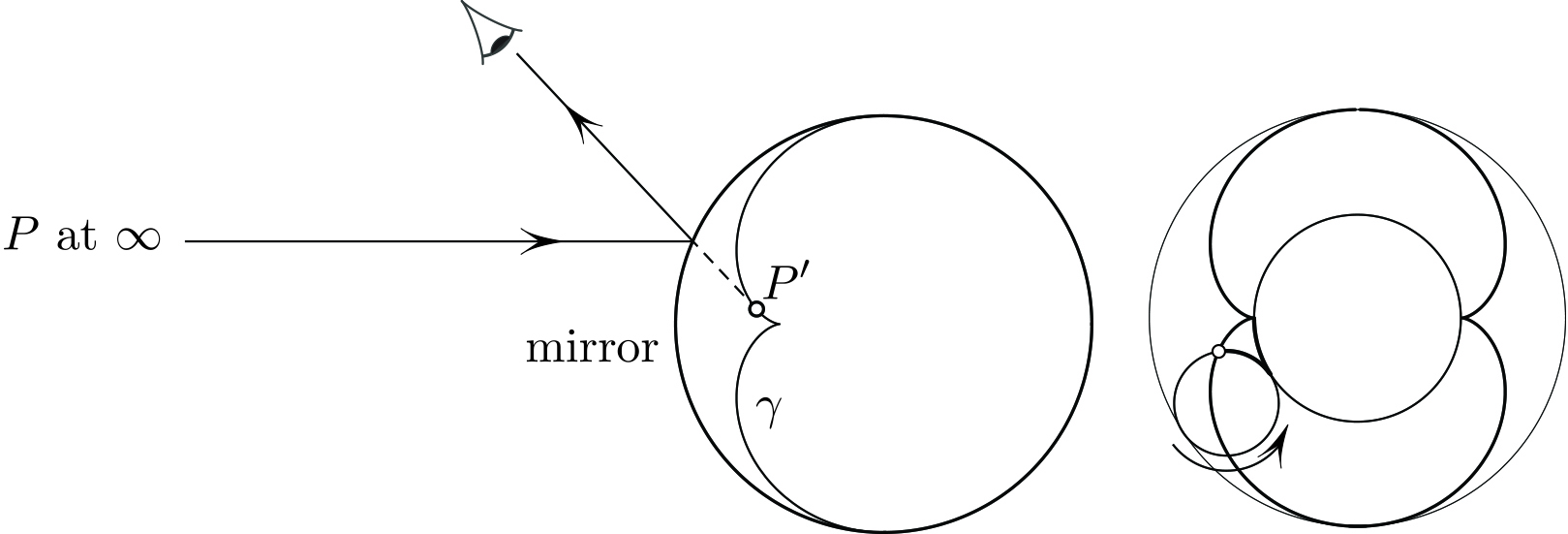
Circles Rolling on Circles The astroid in \((1)\) is a “hypocycloid” — more precisely, a path traced by a point of a circle of radius \(a/4\) that rolls without slippage on the inside of a circle of radius \(a\) (see Figure 2). Interestingly, another kind of cycloid arises as the set of images of a distant object in a circular mirror (see Figure 3). As we walk around a shiny post, the Sun’s reflection inside the post follows the nephroid (more precisely, the left half of it in Figure 3).

<strong>Figure 2.</strong> A circle that rolls on the inside of a larger stationary circle—with a \(\textrm{1:4}\) ratio of radii—generates the astroid.
Figure 2. A circle that rolls on the inside of a larger stationary circle—with a \(\textrm{1:4}\) ratio of radii—generates the astroid.

Cycloids arise in two entirely different settings mentioned here. Is this a coincidence or a manifestation of some more general fact? I do not know. Back to Stretched Astroids Returning to the claim that \(\gamma\) is a stretched astroid, the proof relies on two facts of independent interest (which I also mentioned in the May article): (i) The ratio of the depth of \(P ^\prime\) to that of \(P\) is \[c \frac{\cos^3 \alpha}{\cos^3 \beta},\] where \(\alpha\) is the angle of the above-water ray with the vertical, with \(\beta\) defined similarly underwater, and \(c\) is as before. And (ii): \[\frac{CP^\prime}{CP} =c \frac{\cos^2 \alpha}{\cos^2 \beta},\] where \(C\) is the crossing point (see Figure 1). From (i), (ii), and Snell’s law, one gets parametric equations of \(\gamma\); elimination of the parameter results in the claim.

<strong>Figure 3.</strong> The set of images of an object at infinity (say, the Sun) in a circular mirror is a nephroid — i.e., a (hyper) cycloid generated by a circle that rolls on the outside of a stationary circle with a \(\textrm{1:2}\) ratio of radii.
Figure 3. The set of images of an object at infinity (say, the Sun) in a circular mirror is a nephroid — i.e., a (hyper) cycloid generated by a circle that rolls on the outside of a stationary circle with a \(\textrm{1:2}\) ratio of radii.

This proof is disappointingly algebraic for such a geometrical result. It would be nice to find a more geometrical and insightful proof than the one outlined here.

The figures in this article were provided by the author.

About the Author

Mark Levi

Professor, Pennsylvania State University

Mark Levi (levi@math.psu.edu) is a professor of mathematics at the Pennsylvania State University.