Balancing a Knife, Euler’s Elastica, and the Mathematical Pendulum
While putting dishes in the sink, I tried to balance a knife on the edge of a pot and noticed an interesting effect: the knife balanced, and stably so, if the blade touched the water (see Figure 1). But nothing worked when the pot was empty; the blade was too light.
The Mechanism

Before looking at the photo, one might think that the blade’s buoyancy would make the balancing act even more impossible, thus giving the handle further advantage. So what is responsible for the balance and stability? In Figure 1, the blade lifts some water up above the level of the remaining surface; this creates suction that pulls the blade down. The lifted water is then added to the blade’s weight, and the equilibrium is automatically stable because the restoring suctional torque is an increasing function of the outward tilt (up to a point). Surface tension also pulls the blade down, but this force is negligible. However, the role of surface tension is indispensable in another way — namely in preventing air from entering the space underneath the blade. To test this role, I added dish soap to the water to see if the decreased tension would cause the knife to tip out. At first nothing happened, but I realized that was because the soap simply dropped to the bottom of the pot. When I mixed the soap with some water and then put it in, the knife tipped out. Soap can decrease water’s surface tension by more than half, down from approximately \(72\) dyn/cm.
A Surprisingly Large Force
To estimate the magnitude of the force that is required to break the knife’s contact with the water, let us consider a slightly simpler case: a horizontal plate of area \(A\) touching the water’s surface (our knife is slightly tilted, hence the difference). The force required to break contact with the water turns out to be approximately
\[F = 2A \sqrt{\rho g \sigma }, \tag1 \]
where \(\rho\) is the water’s density and \(\sigma\) is the surface tension; I derive this formula at the end. The force is surprisingly large: for the area \(A = 1m ^2\), it is about \(5\) kg, i.e., roughly \(10\) pounds. In contrast, the surface tension results in the force \(f\) approximately proportional to the plate’s perimeter \(P\):
\[f\approx \sigma P, \]
which is a much smaller quantity than \(F\) for the areas that are the size of our knife.
Euler’s Elastica
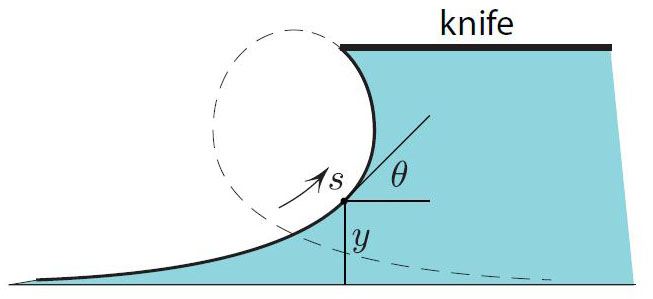
Consider the shape of the water’s surface along the straight edge of the knife in Figure 1, assuming that this edge is also parallel to the surface. Figure 2 depicts the two-dimensional section of this shape, which is governed by the equilibrium condition: Curvature \(\kappa\) is caused by the pressure difference \(p\) between the two sides of the water’s surface1 and is inverse proportional to the surface tension \(\kappa = p/ \sigma\). Since the hydrostatic \(p = \rho gy\) (the excess of the air pressure over water pressure), we have
\[\kappa = c y, \tag2 \]
where \(c = \frac{\rho g}{\sigma }\). The exact same equation describes Euler’s elastica: equilibrium shapes of elastic rods, except that \(c\) can also be negative.
The Pendulum
By differentiating \((2)\) with respect to the arc length \(s\) along the curve and recalling that \(\kappa =\theta ^\prime\) and \(y ^\prime = \sin \theta\) (here, \(^\prime = d/ds\)), we get
\[\theta ^{\prime\prime} = c\sin \theta.\]
This is precisely the equation of the pendulum, with \(\theta = 0\) corresponding to the upside-down (unstable) equilibrium. In other words, if we travel along the curve in Figure 2 with unit speed, the tangent’s direction swings exactly as if it were a pendulum (with gravity pointing to the left in Figure 2). The curve in Figure 2 satisfies \(\theta \rightarrow 0\) as \(s \rightarrow - \infty\) and \(\theta \rightarrow 2 \pi\) as \(s \rightarrow + \infty\). This corresponds to heteroclinic solution of the pendulum equation, with the pendulum approaching the unstable equilibrium in both future and past.
Derivation of (1)
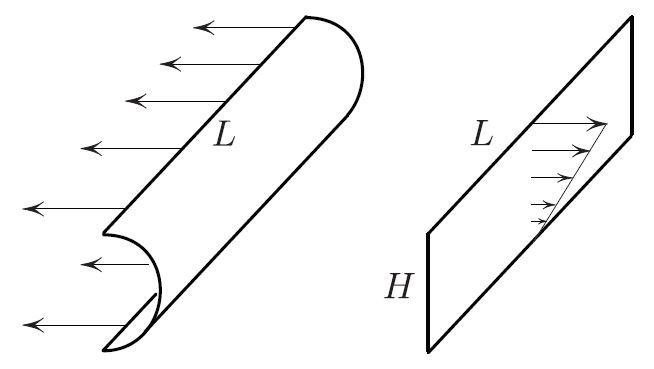
The force \(F\) is the weight of the lifted water of volume \(\approx AH\), where \(H\) is the maximal possible height, so that
\[ F\approx \rho g AH. \tag3 \]
We must find the maximal possible for which the surface tension can still keep the air from under the plate.
According to Figure 3, the equilibrium condition is
\[2 \sigma L = p_{\rm average}\cdot H L.\tag4 \]
After simple algebra, substituting \(p_{\rm average} =\frac{1}{2} \rho g H\) into \((4)\) yields
\[H = \sqrt{ \frac{4 \sigma }{\rho g}}.\]
Substituting this value into \((3)\) gives the lifting force \((1)\). This is the theoretical maximum; the true value may be less because the angle \(\theta\) near the top need not be \(\pi\), as it is in Figure 3.
1 Actually, one could call it the air’s surface with almost equal justification.
The figures in this article were provided by the author.
About the Author
Mark Levi
Professor, Pennsylvania State University
Mark Levi (levi@math.psu.edu) is a professor of mathematics at the Pennsylvania State University.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



