BLIS: Extending BLAS Functionality

A wide range of computational mathematics applications build upon the Basic Linear Algebra Subprograms (BLAS) — a fact that underscores the importance of community software for dense linear algebra (DLA). The BLAS-like Library Instantiation Software (BLIS) project is both a widely used open-source BLAS implementation on central processing units (CPUs) and a toolbox/framework for the rapid instantiation of BLAS-like DLA functionality [5]. The recent 1.0 release of BLIS in May 2024 extended its portability to a wide variety of architectures, including x86-64 (Intel and AMD), ARM (ARM32, AArch64, and Ampere Altra), IBM Power Systems, and RISC-V (especially SiFive X280). In addition, this release significantly expanded BLIS’s multithreading capabilities to support diverse end-user applications and enable scalability to hundreds of cores. BLIS 1.0 also incorporates proposed changes to BLAS that consistently handle exceptions [1], like the propagation of NaN and Inf. Ultimately, the updated software is an excellent open-source solution for all CPU BLAS needs. In fact, readers may already be using BLIS, as it is included in the AMD Optimizing CPU Libraries and NVIDIA Performance Libraries; it is even packaged in major Linux distributions.

But BLIS is so much more than simply a BLAS implementation. Have you ever needed to contort your code to fit the functionality of traditional BLAS? Has the performance, portability, maintainability, or readability of your code suffered as a result? The next major release—BLIS 2.0—will represent a fundamental shift in BLIS’s seamless capability to enable the extension of BLAS to new high-performance operations. Users will be able to implement BLAS-like operations by remixing BLIS’s “building blocks” with specified components. These features are already available for early evaluation ahead of the forthcoming release. In this article, we explore the nuances of BLIS 2.0 and explain its ability to enable high performance and novel capacities with low code complexity.

Portable High Performance

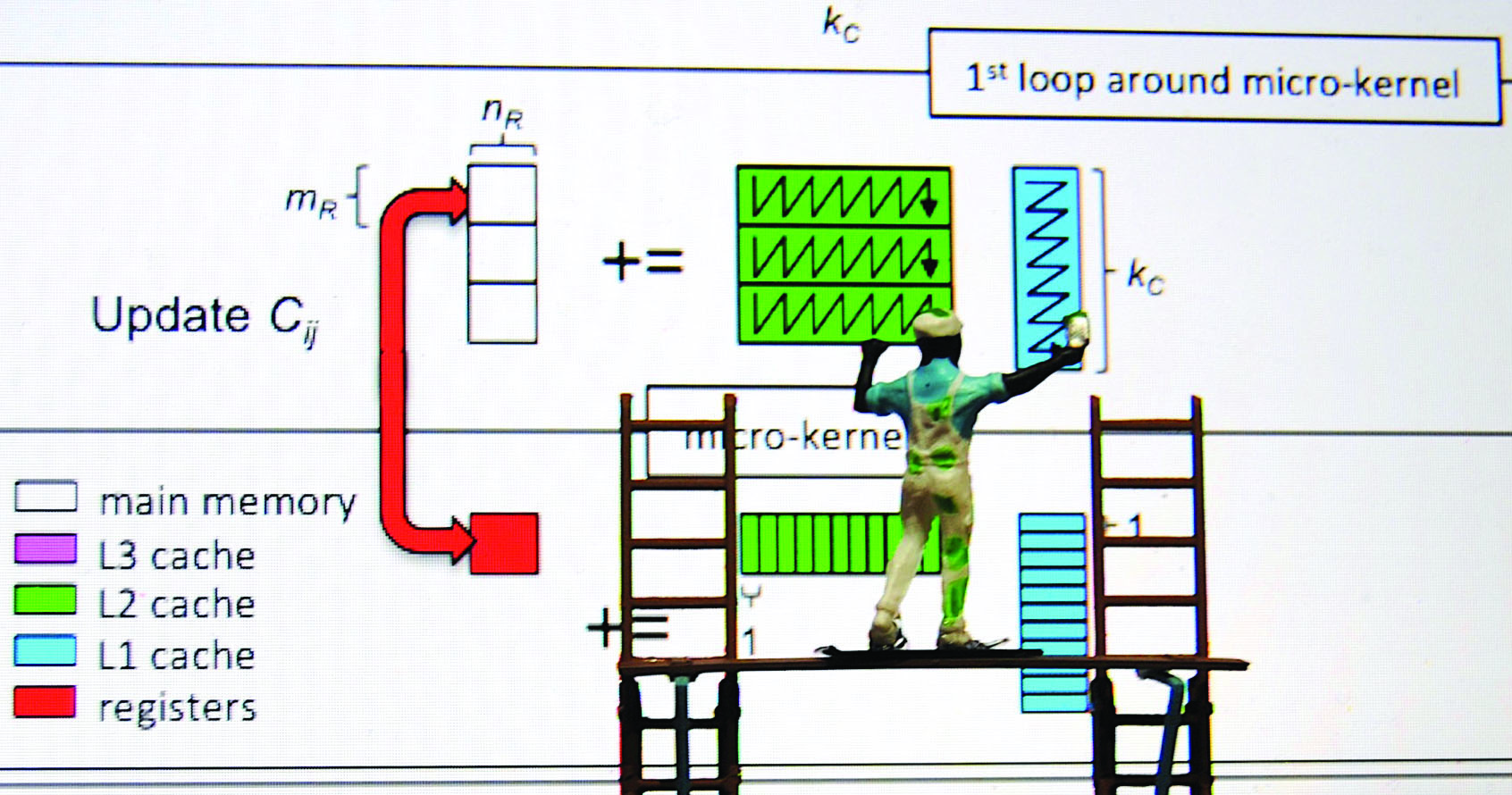
High-performance implementations of the types of operations that BLAS supports require the careful orchestration of data movement between memory layers, amortizing overhead over useful computation. Goto’s algorithm exploits this balance nearly optimally for the matrix-matrix multiplication GEMM operation within Level 3 BLAS. Figure 1 illustrates the implementation of this algorithm in BLIS. For \(C := \alpha A B + \beta C\), the successive partitioning of operands allows for data resuse in caches. Along the way, submatrices of \(A\) and \(B\) are packed to improve data locality. When targeting a new CPU architecture, BLIS only requires a specialized microkernel; all other parts of the algorithm are implemented in ISO C99. The five loops are parallelizable with OpenMP directives or other threading mechanisms. Implementations of related matrix-matrix operations (e.g., other capabilities in Level 3 BLAS) employ a modified version of the same algorithm that takes advantage of special structures in one or more operands.

BLIS Plugins and New Functionality

Modern DLA computations in scientific computing, machine learning, and data science often necessitate BLAS-like operations that—when implemented in terms of traditional BLAS—require extra data movement, workspace, or post-processing efforts from main memory. We can restructure and optimize this BLAS-adjacent overhead by organizing the algorithmic framework to enable the modular incorporation of additional or modified operations.

To support this process, a novel plugin mechanism in BLIS 2.0 lets users define new microkernels, packing routines, or other operations in their own code and easily incorporate these components—along with BLIS-supplied ones—into an innovative BLAS-like operation that retains high performance. A simple application programming interface (API) allows users to tweak existing operations like GEMM or design new algorithms from scratch via BLIS’s control tree abstraction. For example, users can cast the following operations as BLIS plugins:

• “Sandwiched” matrix multiplication operations compute \(C := A X B + C\), where \(X\) might be a diagonal or tridiagonal matrix. BLIS can fuse multiplication by \(X\) into packing, thereby reducing memory traffic and improving performance.
• The computation of \(M = ( X + \delta Y )( V + \epsilon W)\)—followed by the result’s addition to multiple distinct submatrices—is a critical building block for the practical high-performance implementation of Strassen’s algorithm [2]. BLIS can incorporate the linear combination of matrices into the packing; \(M\)'s addition to multiple matrices is a post process in the microkernel.
• Calculation of the \(k\)-nearest neighbors for all points in a \(d\)-dimensional point set is an important primitive in clustering analysis. Previous research used a BLIS-like framework [6] to implement this operation and achieve impressive speedups.
• Tensor contractions arise in machine learning, quantum computing, quantum chemistry, data science, and other fields. A typical implementation requires the costly transformation of data into a GEMM-compatible ordering of elements. Practitioners can fuse this data movement into packing and microkernel post-processing to achieve near-peak performance. The TBLIS tensor contraction library [3] leverages this fact and will employ a BLIS plugin in its next release.

BLIS 2.0 utilizes user-defined plugins to provide support for these and many other extended linear algebra operations. It leverages the core BLIS framework and its performance portability, built-in threading layer, and other features to help users easily and rapidly instantiate high-performance algorithms.

Mixing and Matching Precisions

BLIS 2.0 enables BLAS and BLAS-like operations where one or more operands have different precisions (single, double, etc.) or domains (real or complex). For example, \(C := \alpha A B + \beta C\) may involve double-precision complex matrices \(C\) and \(A\) and single-precision real matrix \(B\), for which the computation should be performed in double-precision arithmetic. The implementation of mixed-precision/mixed-domain capabilities for all Level 3 operations (except TRSM) builds upon the same mechanisms that support plugins. Other planned changes will allow users to register new data types and offer built-in support for low-precision computations, such as bfloat16.

The following key insights tame the exponential growth in combinations within the implementation: (i) Users can incorporate conversions between precisions into the packing that already transpires in Goto’s algorithm, (ii) post-processing can take place within the microkernel, and (iii) users can pack matrix data into appropriate formats that leverage real-domain computation to support the mixing of domains. This three-pronged approach only requires a number of kernels that scales quadratically with the number of data types. As with user-defined plugins, combining the appropriate components permits a small number of explicit kernels to enable a wide range of functionality without changes to the native BLIS interface, wherein an operand’s precision and domain is specified in an object. This flexibility highlights the advantages of APIs beyond the traditional BLAS interface.

Get Involved With BLIS

A vibrant developer and user community greatly bolsters the continued growth of BLIS. The BLIS GitHub page features BLIS releases, documentation, performance data, and examples of further reading. Submit an issue or a pull request, ask a question, or simply give us a “star.” Then, join the more than 200 members of the BLIS Discord server who are eager to discuss BLIS, linear algebra, and scientific computing. Finally, consider attending our upcoming “BLIS Retreat” in late September—an annual event that originated in 2014—for the opportunity to mingle and interact with contributors from academia, industry, and the broader community.

References
[1] Demmel, J., Dongarra, J., Gates, M., Henry, G., Langou, J., Li, X., … Rubio-González, C. (2022). Proposed consistent exception handling for the BLAS and LAPACK. Preprint, arXiv:2207.09281.
[2] Huang, J., Smith, T.M., Henry, G.M., & van de Geijn, R.A. (2016). Strassen’s algorithm reloaded. In SC ’16: Proceedings of the international conference for high performance computing, networking, storage and analysis (pp. 690-701). Salt Lake City, UT: Institute of Electrical and Electronics Engineers.
[3] Matthews, D.A. (2018). High-performance tensor contraction without transposition. SIAM J. Sci. Comput., 40(1), C1-C24. 
[4] Van Zee, F.G., & Smith, T.M. (2017). Implementing high-performance complex matrix multiplication via the 3m and 4m methods. ACM Trans. Math. Soft., 44(1), 7.
[5] Van Zee, F., van de Geijn, R., Myers, M., Parikh, D., & Matthews, D. (2021). BLIS: BLAS and so much more. SIAM News, 54(3), p. 8. 
[6] Yu, C.D., Huang, J., Austin, W., Xiao, B., & Biros, G. (2015). Performance optimization for the \(k\)-nearest neighbors kernel on x86 architectures. In SC ’15: Proceedings of the international conference for high performance computing, networking, storage and analysis (pp. 1-12) Austin, TX: Association for Computing Machinery.