Bypassing Covert Resilience in Contentious Online Networks

Tragic acts of terrorism—such as February’s mass stabbing in Austria by a 23-year-old Syrian asylum seeker who was allegedly radicalized online by the Islamic State [8, 9]—accentuate the dangers of radicalization via the internet. Terrorist organizations exploit popular social media platforms to advance their ideology-driven agendas through recruitment, fundraising, and the spread of propaganda — all of which ultimately causes severe harm in communities around the world. From a national security perspective, this drive towards radicalization raises pressing questions about our ability to monitor, quantify, understand, predict, and even mitigate such efforts before they materialize as tragedies. 

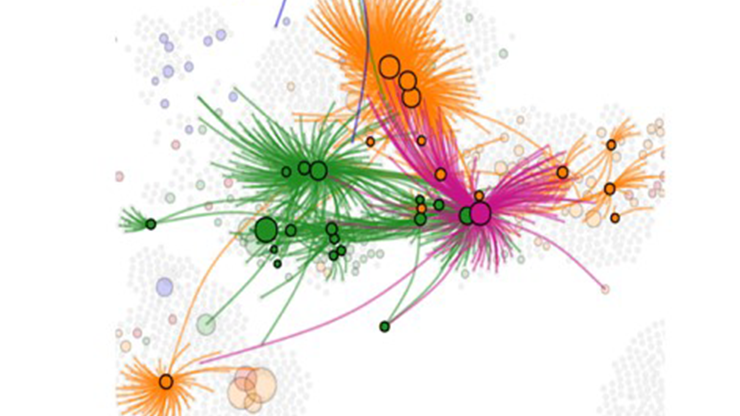
Over the past several years, we have used physics, network analysis, data science, and artificial intelligence to investigate online radicalization. We collected and analyzed large-scale, high-resolution dynamical data from online communities, many of which express support for ideologies that are linked to terrorist activity. We have studied these communities’ behaviors and tactics over long periods of time, across varied dynamical scales, and on different social media platforms where terrorist organizations tend to thrive. Our research has uncovered intriguing resilience strategies that often bypass social media platforms’ security protocols, which would have otherwise permanently banned these online groups (see Figure 1). Quantitatively, we have identified unique statistical patterns in the early dynamics that point to the onset and rapid growth of large-scale ideological movements in the form of a strong online presence; these patterns affirm the influence of terrorist organizations in the online domain and their subsequent connection to violent offline activity [4]. 

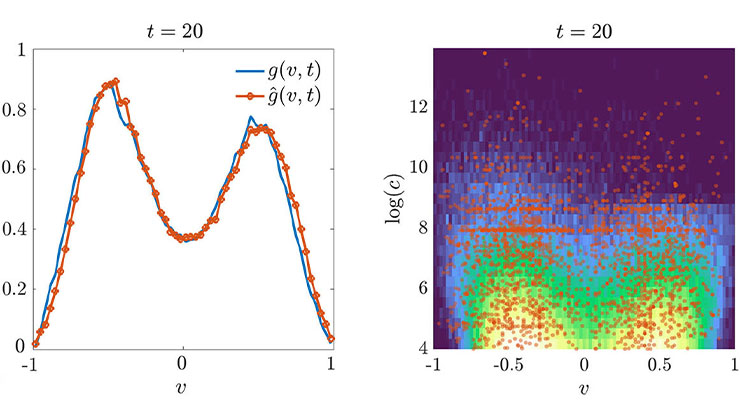
Our data reveals the following takeaways (see Figure 2): 

1. The distribution of online group sizes near the onset follows a power law with an exponent that is equal to \(2.46\) \((p = 0.64)\)
2. The probability that two unlinked online groups of sizes \(s_1\) and \(s_2\) at time \(t\) will be linked at time \(t+1\) is proportional to the product of their sizes \(s_1 \times s_2\)
3. The time-averaged group size distribution follows a similar pattern, where the exponent is equal to \(2.33\) \((p = 0.86)\). 

These statistical patterns serve as the basis for a new first-principles dynamical theory of online aggregation within and across social media platforms [6, 7]. The theory accounts for unique societal features, namely heterogeneity, fragmentation, and a growing user population. Heterogeneity refers to the uniqueness of each user/person and its influence on their behavior within the platform (e.g., joining an ideological online group). Fragmentation is the act of shutting down online communities when social media platform moderators spot activity that violates the guidelines of allowable images, language, and/or conduct. Lastly, a growing population accounts for the increasing number of users that platforms experience every day — i.e., a time-varying population.

At the microscopic level, the actions of dissimilar individuals appear to be of negligible relevance to a macro-level observer (e.g., a moderator) because they are small, sparse, and seemingly unrelated. However, a large number of small interacting cells can merge and—while remaining under the radar—rapidly form a large movement that emerges at seemingly unpredictable times. Our theory quantifies the onset of such movements at the macroscale (i.e., platform level) and the relationship between the group’s heterogeneity and growth rate; it also predicts the size distribution at the onset to be \(2.5\) (akin to empirical pattern 1). To build the theory, we used a merging probability that is proportional to the product of the linking groups’ sizes (akin to empirical pattern 2). When we account for total fragmentation, the time-averaged size distribution follows a power-law distribution with an exponent of \(2.5\) (akin to empirical pattern 3).

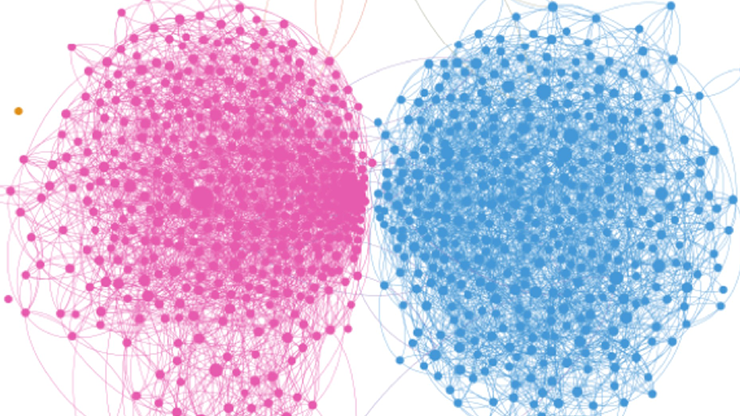
In the context of mathematical physics, our framework constitutes a novel generalization of nonlinear fluid equations with shockwave solutions. For example, if platform moderators do not effectively identify and shut down suspicious groups, and if the population and heterogeneity remain rather invariant, then the resulting equation reduces to the inviscid Burgers’ equation: the simplest nonlinear fluid physics equation that describes a fluid without viscosity. On the other hand, we can add extra terms to the equation—i.e., diffusive terms that are typical of turbulence in viscous fluids—to represent additional interactions. This framework can also accommodate other online mechanisms, such as higher-order interactions that resemble coordination among three or more groups, monomer fragmentation that accounts for users who leave a group due to loss of interest, and shifts in background population due to an influx of new users with opposite ideological alignment [6] (see Figure 3).

In principle, we could use our developed framework to test/guide myriad intervention strategies that seek to bypass covert resiliency in contentious online networks. From a control theory perspective, our findings indicate that the flux of new users and heterogeneity of the platform’s user base can control the onset time and growth curve. More specifically, increasing the flow of new users may hamper a movement’s development at the macroscopic level, and meeting a specific influx rate threshold entirely prevents the movement’s macroscopic formation. In addition, if we impact the individual user’s ideological alignment even slightly, then we can significantly affect the onset time and growth rate of the emerging macroscopic movement. Finally, our framework is expandable in order to consider interconnectivity across different platforms, where the equations take on a tensor form. Using this expansion, we have found good agreement between real complex online data and natural data [3, 5].

More empirical efforts are needed to specifically identify the communities that are best captured by our theoretical analysis and experimentally test the effectiveness of our control strategies. We believe that the good agreement we have attained thus far is a solid first step in this ongoing research journey. Furthermore, we developed our framework in a generic way so that it may apply to many decentralized systems of heterogeneous objects across disciplines [1, 5]. Full details are available in our new textbook [2].

Pedro Manrique delivered a minisymposium presentation on this research at the 2024 SIAM Annual Meeting, which took place in Spokane, Wash., last year.

References
[1] Huo, F.Y., Manrique, P.D., & Johnson, N.F. (2024). Multispecies cohesion: Humans, machinery, AI, and beyond. Phys. Rev. Lett., 133, 247401.
[2] Huo, F.Y., Manrique, P.D., Zheng, M., & Johnson, N. (2025). Introduction to online complexity: The new social physics of extremes, misinformation, and AI. Oxford, UK: Oxford University Press.
[3] Huo, F.Y., Restrepo, D.J., Manrique, P.D., Woo, G., & Johnson, N.F. (2025). Physics reveals and explains patterns in conflict casualties. Europhys. Lett. 
[4] Johnson, N.F., Zheng, M., Vorobyeva, Y., Gabriel, A., Qi, H., Velasquez, N., … Wuchty, S. (2016). New online ecology of adversarial aggregates: ISIS and beyond. Science, 352(6292), 1459-1463.
[5] Manrique, P.D., Huo, F.Y., El Oud, S., & Johnson, N.F. (2024). Non-equilibrium physics of multi-species assembly applied to fibrils inhibition in biomolecular condensates and growth of online distrust. Sci. Rep., 14(1), 21911.
[6] Manrique, P.D., Huo, F.Y., El Oud, S., Zheng, M., Illari, L., & Johnson, N.F. (2023). Shockwavelike behavior across social media. Phys. Rev. Lett., 130, 237401.
[7] Manrique, P.D., Zheng, M., Cao, Z., Restrepo, E.M., & Johnson, N.F. (2018). Generalized gelation theory describes onset of online extremist support. Phys. Rev. Lett., 121, 048301.
[8] Taha, R. (2025, February 16). Austria stabbing 'Islamist attack,' interior minister says. Deutsche Welle. Retrieved from https://www.dw.com/en/austria-stabbing-islamist-attack-interior-minister-says/a-71629831.
[9] Zivulovic, B. (2025, February 17). Austria says stabbing attack suspect swore allegiance to Islamic State. Reuters. Retrieved from https://www.reuters.com/world/europe/three-intensive-care-after-deadly-austrian-knife-attack-2025-02-16.