Challenges and Opportunities of Scaling Up Quantum Computation and Circuits

Rapid advancements in various quantum computing architectures have ignited a sense of cautious optimism about the realization of quantum advantage, especially as the field transitions from predominantly theoretical explorations to more applied functionalities. In addition to addressing challenges that pertain to single quantum bit (qubit) noise, fidelity, and decoherence, vendors are now emphasizing the scalability of their quantum systems as a critical component of their success. Current architectures—including trapped ions, superconducting circuits, and Rydberg atoms—face scalability hurdles in terms of the number of qubits and their fidelity [1]. These hurdles have inspired both academic and industry researchers to develop scaling strategies that are reminiscent of the early (but still relevant) stages of classical supercomputing. Here, we discuss some of quantum computing’s opportunities and challenges in the realms of circuit optimization and scalability.

The design of compact quantum circuits plays an important role in the noisy intermediate-scale quantum (NISQ) computing era and the broader quest for scalable quantum systems. Compact circuits are essential because they enable the efficient use of existing NISQ devices that have a small number of physical qubits, limited connectivity between qubits, and moderate quantum gate fidelity. The design and implementation of compact quantum circuits can maximize the computational power of NISQ devices by permitting users to run larger quantum circuits, thus allowing for the investigation of more realistic problems with the overarching near-term goal of demonstrating quantum advantage. Compact quantum circuits are also crucial for scalability because they reduce the overhead that stems from adding more qubits or gates to a quantum system. Doing so both enables quantum computations on present NISQ devices and paves the way for the eventual construction and deployment of large, fault-tolerant quantum computers — ultimately ushering in a new era of quantum computing that can solve hard optimization problems and address complex challenges across various domains, from cryptography to finance [3].

Current NISQ machines have spawned a class of variational quantum algorithms that aim to solve optimization problems by using an optimization algorithm on a classical computer to adjust the parameters of a quantum circuit. The optimization methods for quantum circuits draw from existing optimization algorithms—such as gradient descent—and require that the quantum devices provide the current state of parameters and the associated gradient vector. In theory, the hybrid quantum-classical algorithm setup should be modular and workable with any optimization algorithm. But in the current era of quantum computing, several issues become apparent when users seek to deploy these systems.

The most challenging component of parameterized quantum circuits (PQCs) is the presence of barren plateaus: regions on the optimization surface that yield low-quality solutions and prevent further optimization. For an \(n\)-qubit quantum circuit that attempts to minimize a cost function \(C(\boldsymbol{\theta})\), the variance of gradient is as follows:

\[\operatorname{Var}\left[\partial_{k} C(\boldsymbol{\theta})\right] \propto\left(\frac{\operatorname{Tr}\left(U^{2}\right)}{2^{3 n}}-\frac{\operatorname{Tr}(U)^{2}}{2^{4 n}}\right), \tag1\]

when any part of the circuit exhibits a unitary \(t\)-design [8]. A unitary \(t\)-design arises when \(U \in \mathbb{U}(d)\) matches the Haar random distribution up to the first \(t\) moments. To better understand quantum \(t\)-designs, consider the expressiveness superoperator

\[\mathcal{A}^{t}(.)=\int_{\mathbb{U}(d)} d U_{H} U^{\otimes^{t}}(.) (U^{\otimes^{t}})^{\dagger}-\int_{\mathcal{U}} d \mathcal{U} U^{\otimes^{t}}(.)(U^{\otimes^{t}})^{\dagger}, \tag2\]

where the first term is computed over the Haar measure and the second is computed with the given quantum circuit [4, 9].

If \(\left|\mathcal{A}^{t}(.)\right|_{2}^{2}=0\), the circuit exhibits a \(t\)-design. Concerningly, these \(t\)-designs occur even for shallow PQCs, and there is no obvious way to alleviate them. Although practitioners have proposed methods like identity initialization or the selection of initial parameters from a better distribution [7], a general solution does not yet exist. The role of optimization algorithms themselves in barren plateaus is an unexplored area of research, and any investigation in this direction could give rise to a proper quantum optimization algorithm and provide insight into the barren plateau phenomenon during the optimization process (as opposed to simply studying initial conditions).

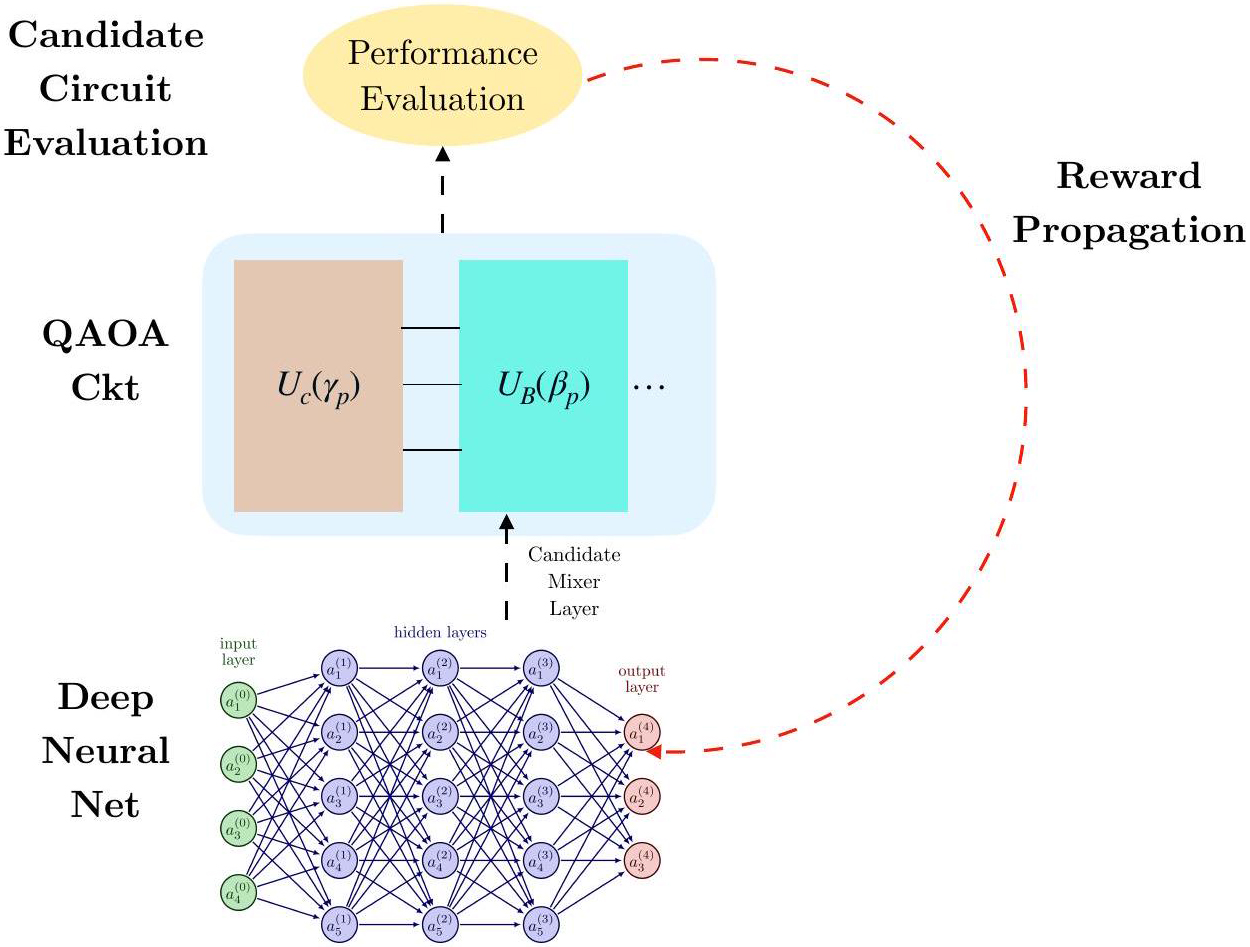
Another angle that seems to promise some relief for the barren plateau problem is the design of algorithms for circuit architecture search that fit within a given constraint — e.g., better performance and less depth (see Figure 1). These algorithms must search for reusable motifs to help find general quantum circuit designs that perform well on a given task while consuming few resources. Improving circuit architecture search may allow researchers to scale the quantum circuit’s processing ability to handle larger, more complex datasets without getting stuck in barren plateaus.

As previously mentioned, a challenging, underexplored direction of variational quantum algorithms is the optimization algorithm’s role in addressing the barren plateau and the scalability of quantum circuits. The current theory of barren plateaus is predicated upon the implicit assumption that the optimizer for parameter updates is itself robust to noise; however, this postulation is often not true in practice. For example, optimizers like stochastic gradient descent and adaptive moment estimation produce suboptimal updates when the gradient is noisy [5]. In contrast, the quantum natural gradient optimizer [10] exhibits much better performance because it computes the Fubini-Study metric tensor for each step of gradient descent. A pure quantum optimizer would take advantage of the structure in quantum density matrices and unitary gates to update parameters, while also requiring fewer measurements and remaining more robust to any type of noise in quantum circuits; the development of such an optimizer would help address the need for scalability in quantum computing. Furthermore, leveraging gradient-free optimization and learning is another underexplored area that could significantly benefit from the insights of classical gradient-free numerical optimization research [6].

The novel adaptive approach to quantum computing allows scientists to design compact quantum algorithms that can adapt to specific problems and NISQ device constraints. This ability is in contrast to traditional quantum algorithms, which are meant to solve general problems and may not be optimal in terms of efficient, compact circuit design. Traditional algorithms often do not account for the shortcomings of NISQ devices, such as the limited number of physical qubits, qubit connectivity, and the fidelity of gate operations.

Although it is still under development, the adaptive approach offers several advantages over traditional quantum algorithms and has been successfully applied in the variational quantum eigensolver and the Quantum Approximate Optimization Algorithm [2, 11]. First, this technique can lead to more efficient and compact algorithms that are tailored to the specific problem at hand. And because the algorithm can adapt to the noise characteristics of the hardware, the adaptive approach is more robust to noise. Users can also modify the algorithm for different hardware constraints, which makes the tactic more flexible than traditional methods. But a downside is that designing compact quantum circuits, which requires an enormous number of gradient evaluations, can be both time consuming and nonscalable.

The scale of problems in the realm of real-life scientific computing, optimization, and machine learning will undoubtedly remain vast, dwarfing even the most optimistic projections for the number of qubits or quantum volume of future architectures. Decomposition algorithms will hence retain their relevance, but the mechanics of communication will likely undergo a transformation. The area of parallelization faces unique challenges and opportunities in this context. The no-cloning theorem states that we cannot create an identical copy of an arbitrary quantum state. Consequently, if a large-scale problem domain is decomposed and separate quantum machines handle its individual parts, the transmittal of information from one quantum processing unit to another via quantum teleportation necessitates the destruction of what has been transmitted at the source. Methods like the EPR pair of qubits for teleportation (named after the Einstein-Podolsky-Rosen paradox) can achieve this transfer with remarkable speed. Consequently, we are on the brink of reimagining parallel computing with the underlying assumption of extremely fast communication, but with the caveat that such communication cannot duplicate arbitrary information. Another largely unexplored area is the use of quantum and hybrid quantum-classical algorithms to initialize classical numerical methods and vice versa. Ultimately, we will continue to encounter new avenues for exploration as we reconsider algorithmic architectures such as multilevel and multiscale algorithms, domain decompositions, domain adaptations, and data reduction.

References

[1] Alexeev, Y., Bacon, D., Brown, K.R., Calderbank, R., Carr, L.D., Chong, F.T., … Thompson, J. (2021). Quantum computer systems for scientific discovery. PRX Quantum, 2(1), 017001.
[2] Grimsley, H.R., Economou, S.E., Barnes, E., & Mayhall, N.J. (2019). An adaptive variational algorithm for exact molecular simulations on a quantum computer. Nat. Commun., 10(1), 3007.
[3] Herman, D., Googin, C., Liu, X., Sun, Y., Galda, A., Safro, I., … Alexeev, Y. (2023). Quantum computing for finance. Nat. Rev. Phys., 5, 450-465.
[4] Holmes, Z., Sharma, K., Cerezo, M., & Coles, P.J. (2022). Connecting ansatz expressibility to gradient magnitudes and barren plateaus. PRX Quantum, 3(1), 010313.
[5] Kingma, D.P., & Ba, J. (2014). Adam: A method for stochastic optimization. Preprint, arXiv:1412.6980.
[6] Kulshrestha, A., Liu, X., Ushijima-Mwesigwa, H., & Safro, I. (2023). Learning to optimize quantum neural networks without gradients. In 2023 IEEE international conference on quantum computing and engineering (QCE) (pp. 263-271). Bellevue, WA: IEEE Computer Society.
[7] Kulshrestha, A., & Safro, I. (2022). BEINIT: Avoiding barren plateaus in variational quantum algorithms. In 2022 IEEE international conference on quantum computing and engineering (QCE) (pp. 197-203). Broomfield, CO: IEEE Computer Society.
[8] McClean, J.R., Boixo, S., Smelyanskiy, V.N., Babbush, R., & Neven, H. (2018). Barren plateaus in quantum neural network training landscapes. Nat. Commun., 9(1), 4812.
[9] Sim, S., Johnson, P.D., & Aspuru-Guzik, A. (2019). Expressibility and entangling capability of parameterized quantum circuits for hybrid quantum-classical algorithms. Adv. Quantum Technol., 2(12), 1900070.
[10] Stokes, J., Izaac, J., Killoran, N., & Carleo, G. (2020). Quantum natural gradient. Quantum, 4, 269.
[11] Zhu, L., Tang, H.L., Barron, G.S., Calderon-Vargas, F.A., Mayhall, N.J., Barnes, E., & Economou, S.E. (2022). Adaptive quantum approximate optimization algorithm for solving combinatorial problems on a quantum computer. Phys. Rev. Res., 4(3), 033029.