Characterizing Musical Sounds with Topological Data Analysis

“Can one hear the shape of a drum?” Mathematician Mark Kac posed this famous question in 1966, and it has intrigued researchers ever since [4]. If you hear the sound of a drum—i.e., the set of overtones that it produces—can you infer its shape? Mathematically, the essence of this spectral geometry question wonders whether one can uniquely determine a shape based on the eigenvalues of the Laplacian operator that is defined on the shape. Many examples of isospectral manifolds are not isometric in settings with two or more dimensions [3]. But the problem is not yet closed, as listeners can indeed discern the shapes of certain geometric types according to their sounds. Kac’s thought-provoking query also impacts a myriad of fields beyond mathematics, including architectural acoustics, audio forensics, pattern recognition, radiology, imaging science, and musical science.

Composers commonly use drum sets with multiple pieces of varying sizes (rather than a single drum) to facilitate a tonic harmonic progression: the foundation of harmony in modern music. Drum sets can train the human brain to distinguish the overtones of individual drums via a comparative training/learning process that teaches listeners to hear the shape of a particular drum from the set.

To create tonal harmony, artisans in ancient China built a set of 65 chime bells—known as the Zenghouyi Bells—that date back to between 475 and 433 B.C.E., in the Warring States Period (see Figure 1a). They designed the shape of each chime bell to produce a distinct sound. The 65 bells gradually vary in size and weight, ranging from 153.4 centimeters (60.4 inches) to 20.4 centimeters (8.0 inches) in height and from 203.6 kilograms (448.9 pounds) to 2.4 kilograms (5.3 pounds) in weight. The Zenghouyi Bells comprise a tonal range from C2 to D7 and can play all 12 semitones in the middle area of the range, thus enabling different melodies, intervals, and temperaments. The same design principle appears in many other musical instruments, such as xylophones (see Figure 1b), pan flutes (see Figure 1c), and pianos (see Figure 1d). Due to the close physical proximity of the chime bells, resonance may occur when they are struck, giving rise to prolonged harmony. Chime bells were traditionally made of bronze—one of the most precious metals of the time—and used in various rituals, ceremonies, and entertainment events.

A fascinating connection exists between the progression patterns of musical instruments and mathematical filtration (see Figure 2a) — a popular technique in modern algebra and topological data analysis (TDA). TDA is a recent branch of applied mathematics that utilizes topological and geometric concepts to understand and extract topological patterns and structures in data. The main workhorse of TDA is persistent homology [2, 6], an extension of algebraic topology that employs filtration to create a mathematical microscopy of a point cloud. Persistent homology delineates the shape of data through comparative analysis of the topological invariant changes that are induced by filtration [6]. When paired with advanced machine learning and deep learning algorithms, it finds tremendous success in the field of data science. Persistent homology has become one of the most powerful tools for simplifying the geometric complexity and reducing the high dimensionality of biomolecular interactions [5], ultimately revolutionizing drug discovery and effectively forecasting emerging viral variants. 

However, persistent homology is not directly applicable to the tonal analysis of chime bells. First, one may regard the collection of chime bells as the result of a set of evolving chime bell manifolds, rather than the result of point cloud filtration. Additionally, no change in topological invariants is associated with the homotopic shape evolution of chime bells. And finally, persistent homology cannot present a frequency or tonal analysis of chime bells or many other musical instruments.

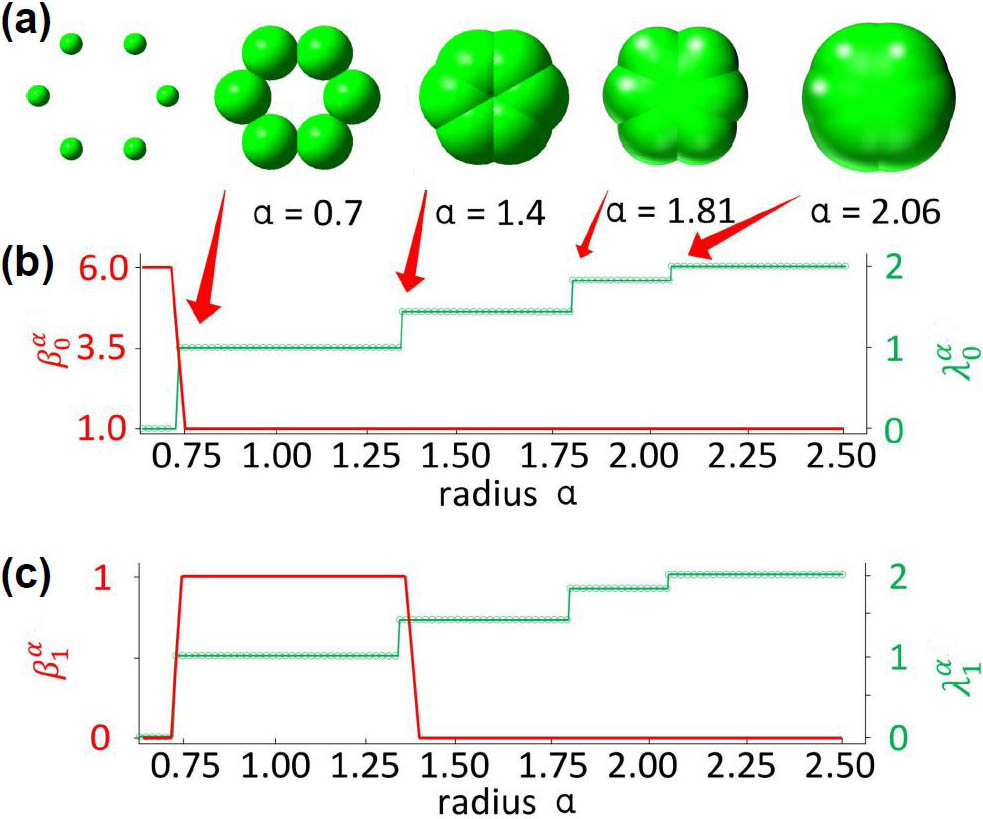
Recently, researchers proposed an evolutionary de Rham-Hodge method [1] as a multiscale generalization of the classical de Rham-Hodge theory: a landmark of 20th-century mathematics. This novel technique provides a multiscale geometric and topological analysis of filtration-induced manifolds; using these manifolds, one can define a family of evolutionary Hodge Laplacians on the set of chime bells to characterize their tonal evolution. In association with a family of de Rham complexes, evolutionary Hodge Laplacians reveal the full set of topological invariants—such as Betti numbers—in their kernel or null space dimensions.

The point cloud counterpart of the evolutionary de Rham-Hodge method on manifolds is called persistent spectral graph (also known as persistent Laplacians) on simplicial complexes [7, 8]. Like the evolutionary de Rham-Hodge method, persistent Laplacians both return the full set of topological invariants in their harmonic spectra (as does persistent homology) and capture the homotopic shape evolution of data during filtration in their first non-harmonic spectra (see Figures 2b and 2c); persistent homology cannot handle this latter task.

Sheaf theory created a generalization of persistent Laplacians, and the resulting persistent sheaf Laplacians enable the embedding of heterogeneous characters in topological invariants (e.g., encoding non-geometric information in a geometry-based simplicial complex) [10]. Persistent path Laplacians—another generalization that is built from the path complex—are designed for directed graphs and directed networks [9]. These new persistent topological Laplacians lay a mathematical foundation for tonal analysis in musical science and significantly extend the applicable domain and power of TDA.

References

[1] Chen, J., Zhao, R., Tong, Y., & Wei, G.-W. (2021). Evolutionary de Rham-Hodge method. Discrete Contin. Dyn. Syst. Ser. B, 26(7), 3785-3821.
[2] Edelsbrunner, H., & Harer, J. (2008). Persistent homology — a survey. Contemp. Math., 453, 257-282.
[3] Gordon, C., Webb, D., & Wolpert, S. (1992). Isospectral plane domains and surfaces via Riemannian orbifolds. Inventiones Math., 110(1), 1-22.
[4] Kac, M. (1966). Can one hear the shape of a drum? Am. Math. Mon., 73(4P2), 1-23.
[5] Liu, J., Xia, K.-L., Wu, J., Yau, S.S.-T., & Wei, G.-W. (2022). Biomolecular topology: Modelling and analysis. Acta Math. Sin. Engl., 38(10), 1901-1938.
[6] Lum, P.Y., Singh, G., Lehman, A., Ishkanov, T., Vejdemo-Johansson, M., Alagappan, M., … Carlsson, G. (2013). Extracting insights from the shape of complex data using topology. Sci. Rep., 3(1), 1-8.
[7] Mémoli, F., Wan, Z., & Wang, Y. (2022). Persistent Laplacians: Properties, algorithms and implications. SIAM J. Math. Data Sci., 4(2), 858-884.
[8] Wang, R., Nguyen, D.D., & Wei, G.-W. (2020). Persistent spectral graph. Int. J. Numer. Methods in Biomed. Eng., 36(9), e3376.
[9] Wang, R., & Wei, G.-W. (2023). Persistent path Laplacian. Found. Data Sci., 5, 26-55.
[10] Wei, X., & Wei, G.-W. (2021). Persistent sheaf Laplacians. Preprint, arXiv:2112.10906.