Coffee and Qubits: A Student Perspective on the 2025 SIAM-Simons Undergraduate Summer Research Program

This past summer, I was honored to participate in the third cohort of the SIAM-Simons Undergraduate Summer Research Program. This program provides funding for 10 undergraduate students to actively partake in applied mathematics and computational science research at various sites throughout the U.S. My research partner, Valentin Garcia, and I spent eight weeks at the University of Hartford; other locations included Duke University, Adelphi University, and Texas State University. In addition to learning about the scientific research process, we honed our communication skills and gained a better understanding of career prospects in applied mathematics, computational science, and data science.

Now that I’ve returned to the University of Washington Tacoma for my senior year of undergraduate education, I continue to notice the program’s many positive impacts on both my research skills and academic confidence. I will be graduating in the spring of 2026 with a B.S. in mathematics, and I feel both excited and prepared for a future career in the mathematical sciences. I wholeheartedly believe that the SIAM-Simons program is a great experience for any undergraduate student who is interested in a career in applied math or a related field, whether it be in academia, industry, or government.

A major benefit of the program is that it covers all costs—including travel, lodging, and meals—and provides participating students with a weekly stipend for other miscellaneous expenses. This generosity helps to eliminate financial barriers that may otherwise prevent undergraduate students from conducting research, making the opportunity accessible to a diverse array of applicants. I was able to devote all of my energy to research instead of worrying about finances, which was invaluable.

Students in the 2025 cohort focused on different topics depending on their assigned location. Research themes ranged from mRNA transport in neuronal cells to deforestation prevention and clustering methods. At our site, Valentin (an undergraduate student at Brown University) and I studied perfect state transfer (PST) and early state exclusion (ESE) in quantum spin chains under the mentorship of Anastasiia Minenkova, an assistant professor of mathematics at Hartford. For the majority of the program, we worked directly with Dr. Minenkova, learning about both the project at hand and the various possible career trajectories for applied mathematicians. Throughout the eight weeks, we also connected virtually with the other 2025 SIAM-Simons participants and attended sessions with guest speakers from academia and industry.

Each day, Valentin and I met with Dr. Minenkova in both the morning and afternoon. These standing meetings enabled us to set a goal for the day, review and work through any assigned articles as background reading, make note of ideas and questions, and reconvene. The flexible structure of the SIAM-Simons Undergraduate Summer Research Program meant that each mentor-mentee group could organize their time as they saw fit, which allowed us to determine how to best collaborate and adapt to the various steps of the research process.

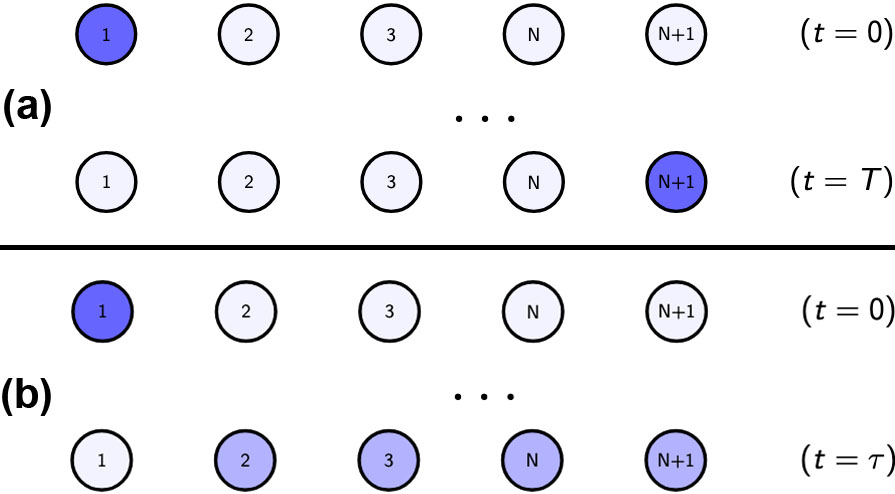
Our particular project involved quantum spin chains, which essentially comprise a one-dimensional row of quantum bits (qubits). We specifically focused on qubits that were experiencing nearest-neighbor interactions. While the interaction process itself is fairly complex, we can think of it as the transfer of the state of one qubit to another. If at some time \(T,\) the state of the first qubit in the chain equals \(0\) and the state of the last qubit equals exactly \(1\), then we say that the quantum spin chain has PST (see Figure 1a). In contrast, if there is a time \(\tau\) before the first instance of PST where the state of the first qubit equals \(0\) and the last is not exactly \(1\), then the chain is demonstrating ESE (see Figure 1b).

We can represent these systems’ Hamiltonians with a tridiagonal persymmetric matrix called a Jacobi matrix. Given the eigenvalues of a system, the corresponding Jacobi matrix is always unique. This useful feature permitted us to reconstruct the matrices from their eigenvalues alone (for context, other matrices may have the same eigenvalues but look completely different).

At the onset of the program, Valentin and I studied the fundamentals of Jacobi matrices and inverse eigenvalue problems. We then generated the matrices by writing code in MATLAB, which was a completely new undertaking for me. I personally found this part of the project to be extremely valuable because I gained firsthand experience with a new coding language that I will undoubtedly utilize in the future. We used the resulting matrices and graphs to note the specific eigenvalues that generated Hamiltonians with and without ESEs.

By the end of the summer, we had proved two theorems about order \(7\) quantum spin chains. First, a Jacobi matrix with positive and negative eigenvalues \(0,\) \(1,\) \(2m,\) and \(2m+1\)—where \(m\) is an integer that is greater than or equal to \(1\)—never has ESE. Second, a Jacobi matrix with positive and negative eigenvalues \(0,\) \(2m+1,\) \(2m+2,\) and \(2m+3\) has ESE \(2m\) times. When not working on these theorems, we drank copious amounts of Dunkin’ iced coffee and explored neat spots around campus and the surrounding area.

In late June, the students from all four locations met up in New York City to visit the Simons Foundation’s Flatiron Institute, where we presented our findings up to that point. This trip to the Flatiron Institute was a key highlight of the program. In addition to networking with each other, we toured the institute and met researchers who are currently working at the cutting edge of applied mathematics right in New York. Each floor of the building was dedicated to a different concentration of applied math, ranging from biology to quantum physics. I left feeling invigorated and knowing that the work I was doing actually has direct implications for many disciplines. Ultimately, however, the most impactful part of the visit was getting to interact with all of the participants in person. It isn’t often that I meet nine other people with the same shared interest as me in one space. Everyone was so passionate and knowledgeable about their topics, and I felt honored to stand next to them and learn from their presentations.

Later in the summer, Valentin and I also presented our results at Mount Holyoke College and spoke with students and professors about their own research endeavors. Mount Holyoke is a private women’s liberal arts college, so it was amazing to meet so many other women who are equally passionate about mathematics.    

Overall, I hope that my reflections help other undergraduate students seize similar opportunities to advance their intellectual prowess, even if such opportunities are out of their comfort zones. The SIAM-Simons program marked many firsts for me: I had never been to Connecticut, never coded in MATLAB, and never been so directly immersed in the field of quantum computing. But I recognized the value of the program and knew that it could positively impact my future, so I applied. In the mere eight weeks that I was in Hartford, my team achieved things that might have otherwise taken multiple semesters; we even published a preprint about our results [1] that has been accepted to SIAM Undergraduate Research Online. I gained invaluable experience, forged lifelong friendships, and connected with colleagues with whom I hope to collaborate in the future. I’m also looking forward to presenting our work at the 2026 SIAM Annual Meeting in Cleveland, Ohio, next July.

References
[1] Escobar, M.G., & Garcia, V. (2025). Early state exclusion in 7-qubit spin chains. Preprint, arXiv:2507.18767.