Conformal Deformation of Conductors

I’d like to describe an observation so simple that it would not be worth mentioning if not for its consequences. \

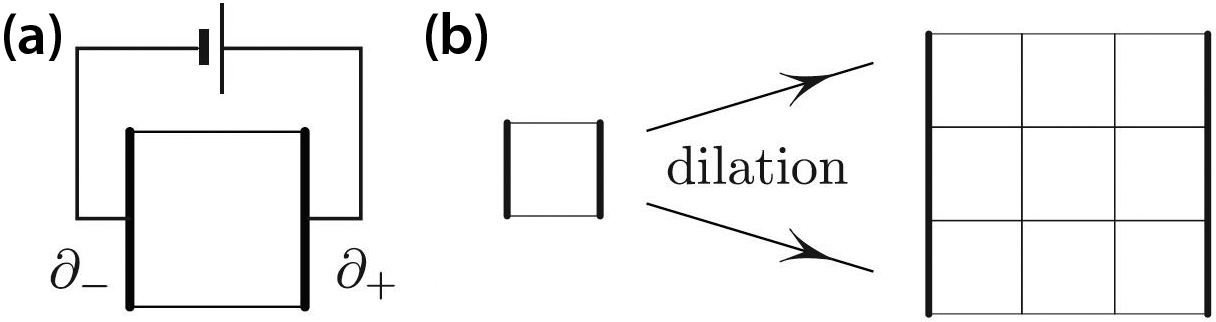
Consider an electrically conducting lamina with constant resistivity \(=1\); this means that if we cut a unit square of the material, the resistance between two opposite sides will be \(1\) unit — say, ohm (see Figure 1a). More precisely, we can coat the opposite sides of the square with a perfect conductor and measure resistance between these conductors. The following property of \(\mathbb{R}^2\) is both trivial and fundamental:

\[\textit{All squares, regardless of size, have the same resistance,}\tag1\]

where the resistance is measured between opposite sides of the square. Figure 1b explains why: putting \(m\) squares in series increases the resistance \(m\)-fold, while putting \(n\) stacks of squares in parallel decreases the resistance \(n\)-fold (in Figure 1b, \(m=n=3\)).

This observation has an immediate implication for conformal maps, since they map infinitesimal squares to infinitesimal squares. Thus,

\[\textit{Electrical resistance does not change under conformal deformation,}\tag2\]

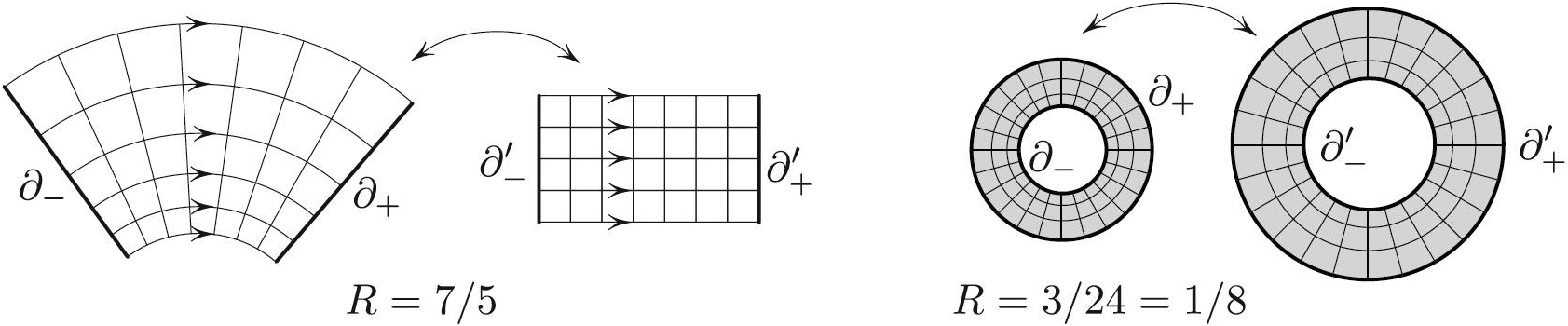
as Figure 2 illustrates. Indeed, let us divide the domain into infinitesimal squares (to make this rigorous, one has to use equipotential lines and the lines of current). The conformal image is then partitioned into infinitesimal squares as well. The map clearly preserves the ratio \(m/n\), where \(m\) is the number of layers and \(n\) is the number of squares per layer. But \(m/n\) is the resistance, so that the resistance is a conformal invariant (we have to take a limit as the squares become smaller, but I skip those details here).

Observation \((1)\) is at the root of the standard theorem in complex analysis, stating that if two annuli are conformally equivalent (i.e., each is a conformal \(1\)-\(1\) image of the other), then the ratios of their radii are the same. Indeed, if one annulus is a conformal image of another annulus, their resistances must be the same according to \((2)\). But the resistance between the two circles bounding the annulus is the logarithm of the ratio of the radii (again skipping the details), so that the ratios are the same for the two annuli.

The conventional name for the resistance is modulus, although “resistance” might be a better term. Another interpretation of the modulus is capacitance, in which case we must replace the current in the conductive lamina with the electrostatic field in the non-conductive plane.

The same electric interpretation of the modulus applies to deformed annuli, i.e., to doubly connected regions. Two such regions are conformally equivalent only if their resistances—measured between the inner and outer boundaries—are equal. And the combinatorial meaning of modulus\(=\)resistance\(=\)capacitance as the limit of the ratio \(m/n\) as \(m,n \rightarrow \infty\) is the same as for the annuli in Figure 2.

The figures in this article were provided by the author.