Control and Integrability in Figure Skating

Figure skating is a popular athletic endeavor, even taking the prime-time slot during televised broadcasts of major sporting events like the Winter Olympic Games. The grace, precision, and elegance of the athletes—in addition to the enchanting effects of dance, music, and costumes—make this sport a perennial favorite for many viewers.

The patterns that skaters carve into the ice have intrigued a wide audience since the 19th century [2]. As a hobby, skaters designed intricate patterns and attempted to trace those designs into the ice. This pastime soon grew in popularity; the patterns became known as “figures” and the hobby was termed “figure skating.” Some of us might still remember televised broadcasts of competitions that included “compulsory figures,” during which athletes could trace patterns at any speed but were only allowed a certain number of pushes off the ice. These contests are not part of official competitions anymore; they have separated into an independent branch with its own events that differ from mainstream Olympic-style figure skating.

While the acrobatic dance programs and jump-filled free skate performances of mainstream figure skating are certainly more spectacular for viewing—and more challenging athletically—the mathematical descriptions of continuous skating paths are just as interesting. Skaters control their motion by changing the direction of their skates and the position of their arms, legs, and torso, thus altering the moments of inertia and location of the center of mass. Such control is produced in the body’s frame, whereas the figures are traced on ice — the coordinate frame fixed in space (spatial frame). The exact nature of the mechanism that a skater employs by mapping the body to the spatial variables—which one achieves with years of careful practice—is very complex and not well understood. This lack of understanding is evident in figure skating instructional methods. For example, each figure skating element can be executed in many ways. Different body positions are considered “optimal” depending on the execution technique of the element in question. When learning a new element, skaters often experiment with technique and try to simply remember the physical feeling of a successful attempt in order to recreate the success (rather than determining the physics behind the attempt). The level to which skaters analyze their movements and the resulting impact on the physical properties varies based on the individual, but significantly examining this relationship is not a common practice.

Though one can technically derive a full mathematical model of a skater on ice, such a model is hardly informative for theoretical understanding. The model would have to incorporate the motion of the head, torso, and every limb — all controlled simultaneously. This challenging problem is likely a good candidate for modern machine learning methods, such as reinforcement learning. However, we are interested in understanding the problem by designing the simplest realistic mechanical model as possible. We focus on the skater’s motion without the blade’s friction with ice, which is a reasonable assumption for a description of the motion on short to intermediate time scales.

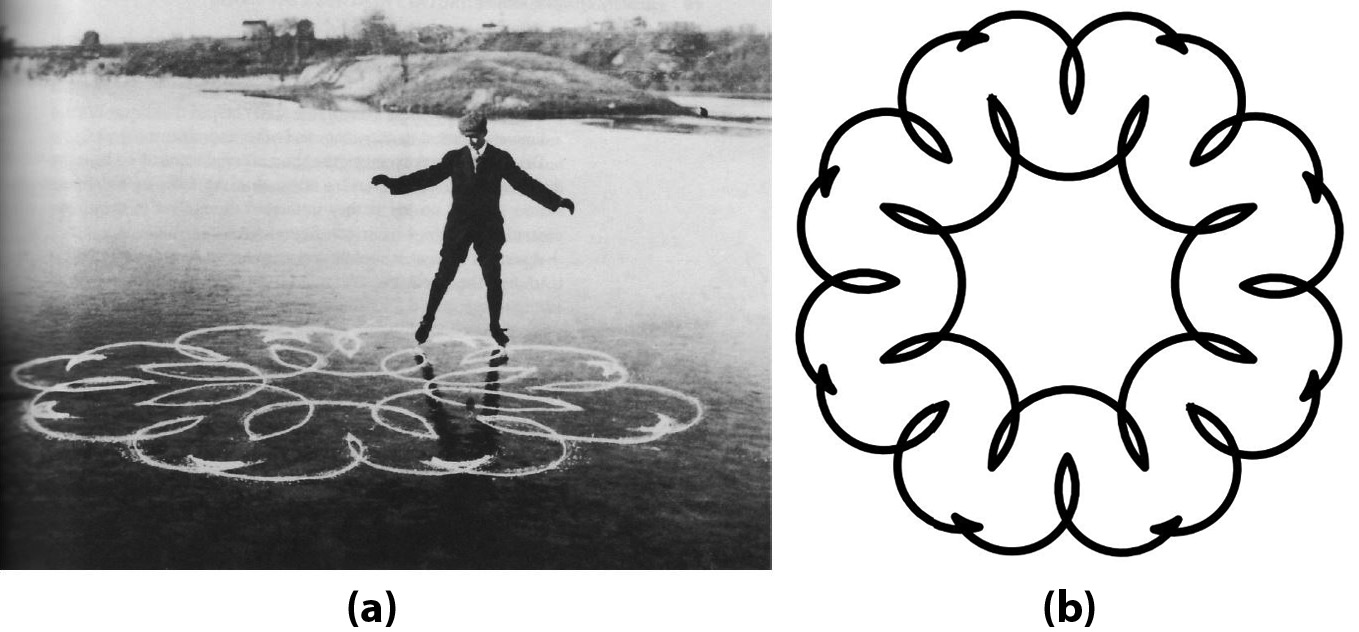
During the continuous motion of a skater on ice, the skate in contact with the ice can only move in the direction of the blade. When the skate turns with respect to the ice, the direction of motion also changes. There is thus a constraint on the velocities of the skate on ice. One cannot write the skate velocity constraint in terms of coordinates only, meaning that the mechanical system that describes the skater belongs to the field of nonholonomic mechanics [1]. This is in contrast to holonomic mechanical systems, which are defined by the property that allows all constraints to be written as a function of coordinates only. Studies of the fundamentals of mechanics, and thus our intuition about mechanics, mostly pertain to holonomic systems. Nonholonomic mechanics can be quite counterintuitive for an unfamiliar reader. For example, the famous Noether theorem of classical mechanics—which connects conservation laws with symmetries—is generally not valid in nonholonomic cases, except for energy conservation [5].

One of the earliest, most famous, and perhaps most pedagogical examples of a skater-like system is the Chaplygin sleigh [3, 4] — a flat, rigid object on ice with a fixed blade (a modern exposition is available in [1]). It is actually one of very few examples of integrable nonholonomic systems [7]. One can understand the Chaplygin sleigh as a two-dimensional model of a skater that lacks the ability to lean. When the position of the sleigh’s center of mass and its moment of inertia are changing, the sleigh is akin to a figure skater who controls their motion by changing the position of their torso and limbs.

Previous researchers have explored the idea of controlling the Chaplygin sleigh motion by altering the position of its center of mass [8]. The question is: How can we control the sleigh to produce a predetermined curve on the ice, as if the sleigh were participating in a figures competition? For example, how can we achieve a typical shape from the figures competition in Figure 1a? The trajectory is not smooth at the “cusp” points. At these points, the skate’s velocity with respect to the ice must be zero, and an experienced skater can perform a quick turn of the skate to continue the motion. To realize this motion in the Chaplygin sleigh, one can build up the trajectory from predetermined “patches”—e.g., pieces of a circle—with vanishing velocity at the ends and connect them with a quick turn at the cusp (see Figure 1). Notice that no push is necessary at the cusp; the skater simply reverses the direction of motion from forward to backward or vice versa.

Things get more complex if one seeks to describe a skater’s motion in three dimensions when there is a possibility for a side lean while skating. If the skater is static (i.e., not moving the parts of their body), this assumption allows a reduction of the mechanical system that describes the skater to a system of seven equations with seven unknowns: linear velocity of the skate; tilt angle; angular velocities of rotation about both the vertical and the blade; and three Lagrange multipliers that describe the reaction of constraints of ice contact, no forward tilt, and the nonholonomic constraint of the skating condition [6]. The system’s mechanical energy is conserved, as expected with the absence of friction. If the projection of the skater’s center of mass onto the blade coincides with the contact point (i.e., a balanced skater), two more constants of motion exist. We can understand one of them as the system’s angular momentum around the vertical axis, and the second as having no physical relevance.

Given these three constants of motion, the system is integrable and constitutes an additional and highly nontrivial example of an integrable nonholonomic system [7]. If the skater is unbalanced—i.e., the projection of the center of mass on the blade’s direction does not coincide with the point of contact—the motion is chaotic with a positive Lyapunov exponent of diverging trajectories. In terms of ice trajectories, the blade’s motion on ice is either quasi-periodic in the integrable case (see Figure 2a) or chaotic in the non-integrable case (see Figure 2b). Just as with the Chaplygin sleigh, the linear velocity of the skate at the cusps goes smoothly through zero and the skater reverses their direction of motion.

It seems plausible to conjecture that experienced figure skaters adjust their positions to choose the integrable case for their performances, moving from one integrable case to another for better control. If correct, this conjecture can help us better understand the algorithms that our own minds use to control the motion — ultimately achieving a precise output in a motion as complex and non-intuitive as figure skating.

This article is based on Vakhtang Putkaradze’s invited presentation at the Second Joint SIAM/CAIMS Annual Meeting, which took place virtually last year. Putkaradze received the 2020 CAIMS-Fields Industrial Mathematics Prize.

References

[1] Bloch, A.M. (2003). Nonholonomic mechanics and control. In Interdisciplinary applied mathematics (Vol. 24). New York, NY: Springer Science & Business Media.
[2] Browne, G.H. (1900). A handbook of figure skating arranged for use on the ice. Springfield, MA: Barney & Berry.
[3] Carathéodory, C. (1933). Der schlitten. ZAMM J. Appl. Math. Mech., 13(2), 71-76.
[4] Chaplygin, S.A. (1911). On the theory of the motion of nonholonomic systems. Theorem on the reducing factor. Mat. Sbornik, 28(2), 303-314.
[5] Fassò, F., Giacobbe, A., & Sansonetto, N. (2012). Linear weakly noetherian constants of motion are horizontal gauge momenta. J. Geom. Mech., 4(2), 129-136.
[6] Gzenda, V., & Putkaradze, V. (2019). Integrability and chaos in figure skating. J. Nonlin. Sci., 30, 831-850.
[7] Kozlov, V.V. (1985). On the integration theory of the equations in nonholonomic mechanics. Adv. Mech., 8, 86-107.
[8] Osborne, J.M., & Zenkov, D.V. (2005). Steering the chaplygin sleigh by a moving mass. In Proceedings of the 44th IEEE conference on decision and control (pp. 1114-1118). Seville, Spain: IEEE.