Cosine Addition Formula and Perpetual Motion

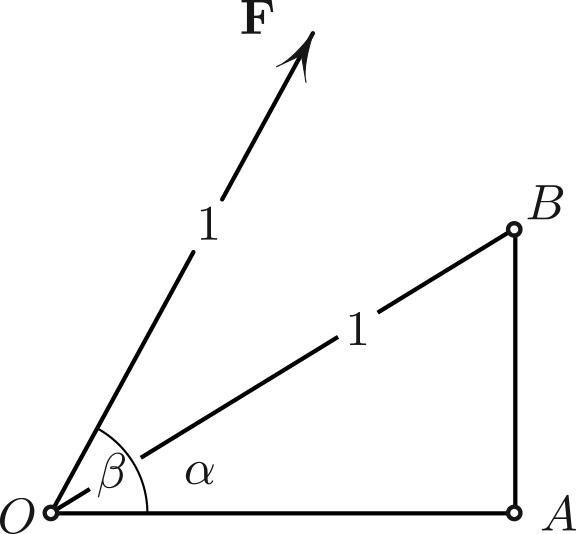
Here is a simple physical interpretation of the familiar identity

\[\cos (\beta - \alpha ) = \cos \beta \cdot  \cos \alpha + \sin \beta \cdot\sin \alpha.\tag1\]

Consider a right triangle \(OAB\) with a hypotenuse of length \(1\), along with the constant force field \(\bf {F}\) of unit vectors that form angle \(\beta\) with \(OA\) (see Figure 1). We can think of \(\bf {F}\) as the constant gravitational field that is viewed in an inconveniently rotated frame.

The work done by \(\bf {F}\) around any closed path vanishes. Indeed, otherwise we could build a perpetual motion machine by moving a particle around a closed path that is oriented so that the work done by \(\bf {F}\) is positive, thus getting free energy. For the closed path \(\Delta OAB\) in particular, we have

\[{\rm work}_{OB}={\rm work}_{OA}+{\rm work}_{AB}.\tag2\]

This equation is the identity \((1)\) in disguise.

Indeed, since the work is given by the force’s component in the direction of displacement multiplied by displacement length, we have \({\rm work}_{OB} = 1\cdot \cos (\beta - \alpha)\), \({\rm work}_{OA} = \cos \beta \cos \alpha\), and \({\rm work}_{AB} = \sin \beta \sin \alpha\). Therefore, \((2)\) amounts to \((1)\) as claimed.

Each of the three terms in \((1)\) acquires physical meaning, just like in \((2)\).

Depending on one’s standards of rigor, the aforementioned expression might be considered a proof. I did not strive for full rigor, trying to keep this piece short.