COVID-19: Models, Mathematics, and Myths

“All models are wrong, but some are useful.” In this quote, British statistician George E.P. Box suggests that while models attempt to predict the performance of certain phenomena, they are subject to limits that may prevent them from representing the true behavior. For example, researchers have introduced mathematical models of varying complexity over the past several months to capture different aspects of COVID-19’s dynamics, with limited to no implications for healthcare decision-makers. Why is this the case? We believe that several myths surround mathematical models that attempt to address COVID-19, and we share them here.

Myths Pertaining to Epidemiological Rates

The nonlinear dynamical models associated with disease spread are contingent upon multiple mechanisms, such as daily infection rates (which in turn depend on contact rates) and daily recovery rates. These factors are extremely dependent on the average contact rate, which varies daily based on the implementation of non-pharmaceutical interventions (like social distancing, lockdown, and facemasks). Due to the drastic changes in these variables over time, it is often impossible for researchers to truly estimate and capture these rates with precision. Moreover, the epidemic curve can only flatten if the recovery rate becomes larger than the models’ infection/transmission rate. One could thus say that disease dynamics depend heavily on transmission heterogeneities, which are often driven by demography, social behavior (e.g., mixing and movement behaviors), and interventions. Many studies have emphasized disease-related implications based on the basic reproduction number, $R_0$, which results when one linearizes the system that is associated with the model in question. This linearization dilutes the role of heterogeneities and is therefore only effective for short-term prediction.

Myths About Flattening the Curve

While many people believe that “flattening the curve” is the best way to slow the spread of coronavirus, one must also account for this method’s impact on the healthcare system capacity — something that even the most sophisticated COVID-19 models tend to ignore. It is likewise valuable to recognize that simpler models can sometimes provide just as much—if not more—insight into healthcare capacity needs as sophisticated models. Consider the following back-of-the-envelope Fermi calculation, which is an effective pedagogical approach that was introduced by physicist Enrico Fermi. This method is characterized by neglecting to present all of the information that one would supposedly need to solve a given problem, which would be difficult to explain with more specialized methods [1].

On average, we are experiencing about $\mathrm{200,000}$ new cases of COVID-19 in the U.S. each day. Roughly 20 percent of acute patients ($\mathrm{40,000}$ individuals) are hospitalized daily [6]. On average, a COVID-19 patient remains in the hospital for around two weeks ($14$ days) [5]; for all acute admitted patients, this calculation equals about $\mathrm{600,000}$ hospital patient days. Given that there are approximately $\mathrm{6,000}$ hospitals in the U.S., each hospital must have roughly $100$ beds fully available for acute COVID-19 patients. In 2018, the pre-COVID-19 occupancy rates for U.S. hospitals were around 65 percent. If we project similar numbers and consider that there are about $\mathrm{900,000}$ beds available in the $\mathrm{6,000}$ U.S., hospitals, this yields about $50$ beds per hospital for COVID-19 patients — which is about half the number of beds that are actually needed.

Myths in the Calculation of $R_0$ 

In mathematical epidemiology, $R_0$ is defined as the average number of secondary infections that are produced by a typical case of an infection within a population where everyone is susceptible. While it is important to understand this number, it is also important to understand whether we are referring to the reproduction number that is calculated at the start of an outbreak versus any time during the outbreak. In other words, when the population is almost completely susceptible at the beginning of an outbreak, we calculate the basic reproduction number $R_0$. But in a population where less than 100 percent of individuals are susceptible, we are really calculating the effective reproduction number.

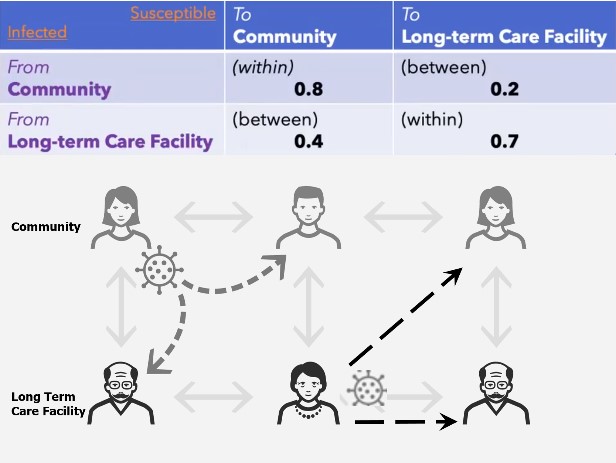
Another misconception related to $R_0$ emerges when multiple groups interact. For example, consider the dynamics in a town that includes a community and long-term care facility (LTCF). Disease transmission occurs within the community, from the community to the LTCF, from the LTCF to the community, and within the LTCF. Suppose the value of $R_0$ is due to the interaction within and between a community and LTCF, as in Figure 1. Beginning with an infected community population of $\mathrm{1,000}$ and an infected population in the LTCF of $100$, one can compute the secondary infections for the community as $0.8\times \mathrm{1,000}+$$0.2\times 100=820$ and the LTCF as $0.4\times \mathrm{1,000}+0.7\times 100=470$, thus yielding a total of $\mathrm{1,290}$ new secondary cases. Calculating the $R_0$ of the population that consists of both the community and LTCF yields $R_0=1.1$ for the entire town-based interaction, which gives more secondary cases $(\mathrm{1,290})$ than initial infections $(\mathrm{1,100})$. While the numbers in Figure 1 suggest that no outbreak exists, our calculations indicate a high likelihood of a major outbreak.

Myths Surrounding Compartmental Epidemiological Models 

Modelers often struggle to select an appropriate model for prediction. In many modeling studies, researchers aim to choose a model and indirectly estimate its unknown parameters with reported disease incidence data (i.e., time series that represent the number of reported daily/weekly cases). One can address the model selection problem in multiple ways; here we provide one simple approach. This methodology of model selection involves collecting a set of models and estimating two quantities—the number of estimated parameters and sum of residuals from the model’s fit to the incidence data—for each model in the set. One can then carry out a simple back-of-the-envelope calculation using the Akaike information criterion (AIC) for each model. A model’s AIC is given by $n\times \log (rss)+2K$, where $K$ is the number of model parameters for estimation, $n$ is sample size of the data, and $rss$ is the ratio of the residual sum of squares [3].

For a typical susceptible-infectious-recovered (SIR) epidemic model, suppose that we only estimate the transmission rate. Let us also estimate the transmission rate and parameter that corresponds to latency for a susceptible-exposed-infectious-recovered epidemic model [4]. We can then readily compute the AIC for both models. A lower AIC value indicates a better model fit. This kind of knowledge could certainly help mathematical modelers as they build new models. The AIC also provides additional information that can help modelers interpret how well each model fits the given data. For interpretation, one computes the $\mathrm{\Delta }\text{AIC}$: the relative difference between the best model $(\mathrm{\Delta }\text{AIC}=0)$ and the others in the set. If $\mathrm{\Delta }\text{AIC}<2$, there is substantial evidence for the model; if $3<\mathrm{\Delta }\text{AIC}<7$, there is less support for the model; and if $\mathrm{\Delta }\text{AIC}>10$, the model is unlikely [2].

Myths About Understanding Vaccination and Herd Immunity 

Modeling the optimal rollout of a vaccine is currently of great interest. If a certain proportion of a population is immune (either by recovering from natural infection, if that grants immunity, or through vaccination), a community can achieve herd immunity — which scientists believe occurs when approximately 70 percent of the population is immune. Consider a group with one infected person, $10$ susceptible individuals, and $R_0=2$. On average, two of these $10$ individuals will contract the disease (i.e., a 20 percent chance of infection). Now assume that two individuals are vaccinated, which provides complete immunity. This means that $0.2\times 8$ of the $10$ people, or $1.6$, will be infected (each of the remaining eight individuals still has a 20 percent chance of infection). The vaccination has hence effectively reduced the reproduction number from $R_0=2$ to $R_0=1.6$.

We know that $R_0$ should be brought below $1$ to control an outbreak. Suppose that a number $V$ of those $10$ people are vaccinated. Since 20 percent of the $(10-V)$ unvaccinated individuals have a chance of infection on average, $0.2\times (10-V)$ of individuals will become infected. In order to control the epidemic, the average number of new infections must be $1$. We thus need to find the value of $V$ that satisfies $0.2\times (10-V)=1$. According to this calculation, vaccinating five out of every 10 people will effectively reduce this disease’s $R_0$ to $1$.

We can generalize this computation for different value of $R_0$. If we assume that each infected person contacts $N$ new people per infectious period, then an average of $R_0/N$ of those individuals will get infected. But if $V$ signifies the number of vaccinated individuals among $N$ contacts, $(R_0/N)\times (N-V)$ represents the number of new infections. If we set this number equal to $1$, we can easily calculate the proportion of individuals who must be vaccinated: $V/N$. This calculation yields $V/N=1-1/R_0$, which is called the herd immunity threshold. If the vaccine effectiveness is $f$ (i.e., a fraction $f$ of vaccinated individuals will be fully protected against infection), then this formula becomes $V/N=(1-1/R_0)/f$. Note that the Pfizer vaccine was found to be 95 percent effective against COVID-19 in clinical trials. 

Concluding Thoughts

Having highlighted the aforementioned five myths, we then asked ourselves, "To what extent is each myth addressed in existing models?" We offer four potential answers to this question.  First, COVID-19 is new and not completely understood. Facing pressure to inform public health decision-making efforts, modelers embraced analogs from other communicable diseases, which may have flaws in hindsight. Second, the models were appropriate given the scientific knowledge at the occasion of their creation; however, our understanding of COVID-19 increases over time, necessitating the inclusion of more refined and/or sophisticated mathematical assumptions. Third, the novel coronavirus is constantly changing, meaning that the clinical presentation of COVID-19 that emerged a year ago is different from the present-day disease. Fourth, the models were actually robust, accurate and—to quote George Box—"useful," but society's rush to adopt the models and their resulting insights fostered a natural, human tendency to downplay the inherent limitations of each model. In essence, society was captivated by the results at the expense of critiquing the details. The myths and challenges that surround existing COVID-19 models are likely a combination of all of the aforementioned points!

In summation, we applaud the work of our peers who are attempting to model the COVID-19 pandemic. Their insights have informed the reactions of both society and the healthcare system. At the same time, we recognize that Box's quote stands firm. 

References

[1] Ärlebäck, J.B., & Bergsten, C. (2013). On the use of realistic Fermi problems in introducing mathematical modelling in upper secondary mathematics. In R. Lesh, P.L. Galbraith, C. Haines, & A. Hurford (Eds.), Modeling Students' Mathematical Modeling Competencies (pp. 597-609). Dordrecht, Netherlands: Springer.
[2] Burham, K.P., & Anderson, D.R. (2002). Model selection and multimodel inference: A practical information-theoretic approach. New York, NY: Springer. 
[3] Glen, S. (2015, September 7). Akaike’s information criterion: Definition, formulas. Retrieved from https://www.statisticshowto.com/akaikes-information-criterion.
[4] Hethcote, H.W. (2000). The mathematics of infectious diseases. SIAM Rev, 42(4), 599-653.
[5] Rees, E.M., Nightingale, E.S., Jafari, Y., Waterlow, N.R., Clifford, S., Pearson, C.A.B., …, Knight, G.M. (2020). COVID-19 length of hospital stay: A systematic review and data synthesis. BMC Med, 18(270).
[6] World Health Organization (2020, March 17). Coronavirus disease (COVID-19): Similarities and differences with influenza. Retrieved from https://www.who.int/news-room/q-a-detail/q-a-similarities-and-differences-covid-19-and-influenza.