Data Assimilation in Medicine
Medicine is an ongoing forecasting process with sparse, inaccurate data. Practitioners rarely employ physiologic knowledge in actual medical practice because of limited data, imperfect models, and a disconnect between measurable variables and potential treatments. Nevertheless, the medical community is currently clamoring for effective employment of precision medicine, which involves providing the right treatment to the right patient; physiology can inspire the solution. We aim to apply current physiologic models—e.g., mechanistic ordinary differential equation (ODE) models of physiology—to medical data to produce useful forecasts. This approach requires fundamental changes to the way in which researchers merge models and data.
Consider the use of inference methods to estimate model states and parameters and evaluate the performance of predictions relative to actionable decisions. One can handle this coupling naturally via data assimilation (DA), a collection of deterministic and stochastic inference methods that estimate and forecast states and parameters of ODE-like models with individual patient data [7]. However, real patient data—which are often sparse and nonstationary—are particularly difficult to use, thus making both inference and model evaluation highly complex. Application to medicine is therefore not possible without model validation and verification that is anchored to clinical consequence. Mathematical innovations must address these realities, and the pursuit of methods that generate actionable knowledge within clinical-specified constraints provides an exciting and deep well of new problems.
One of the human endocrine system’s many tasks is to maintain healthy glucose levels. When someone consumes carbohydrates (fat and protein have secondary effects), the carbohydrates are converted to sugar and absorbed by the gut; this causes glucose levels to rise. In response, the pancreas releases insulin, which facilitates glucose uptake for metabolism and makes blood glucose levels fall. As glucose concentrations return to baseline, the liver releases stored glucose to maintain the baseline concentrations. Glucose levels become elevated when the endocrine system is compromised, leading to acute and chronic harm that significantly reduces the quality and length of life.
Diabetes mellitus (DM) is a catch-all for many functionally different diseases that induce elevated glucose. It comprises type II diabetes (91 percent), type I diabetes (six percent), and other diseases (three percent). While DM is multifactorial, the primary defects include insulin resistance and insufficiency. In other contexts—e.g., the intensive care unit (ICU), where 80 to 90 percent of patients’ endocrine systems cannot maintain healthy glucose levels—additional defects like stress hormones, kidney and liver damage, and gut absorption contribute to elevated glucose. Operationally, practitioners achieve glycemic management via trial and error; they utilize generic guidelines to direct administration of medications such as metformin and insulin, approach dosing conservatively, and iterate management until the patient is stable.
Computational approaches for quantitative glucose forecasting and control have largely focused on the artificial beta cell/pancreas project, a closed-loop insulin delivery system for patients with type I diabetes. The artificial pancreas represents a significant advance in the clinical practice of glucose management and is currently in clinical trials. Researchers have taken similar approaches without control for type II diabetes, but these methods remain underdeveloped [2].
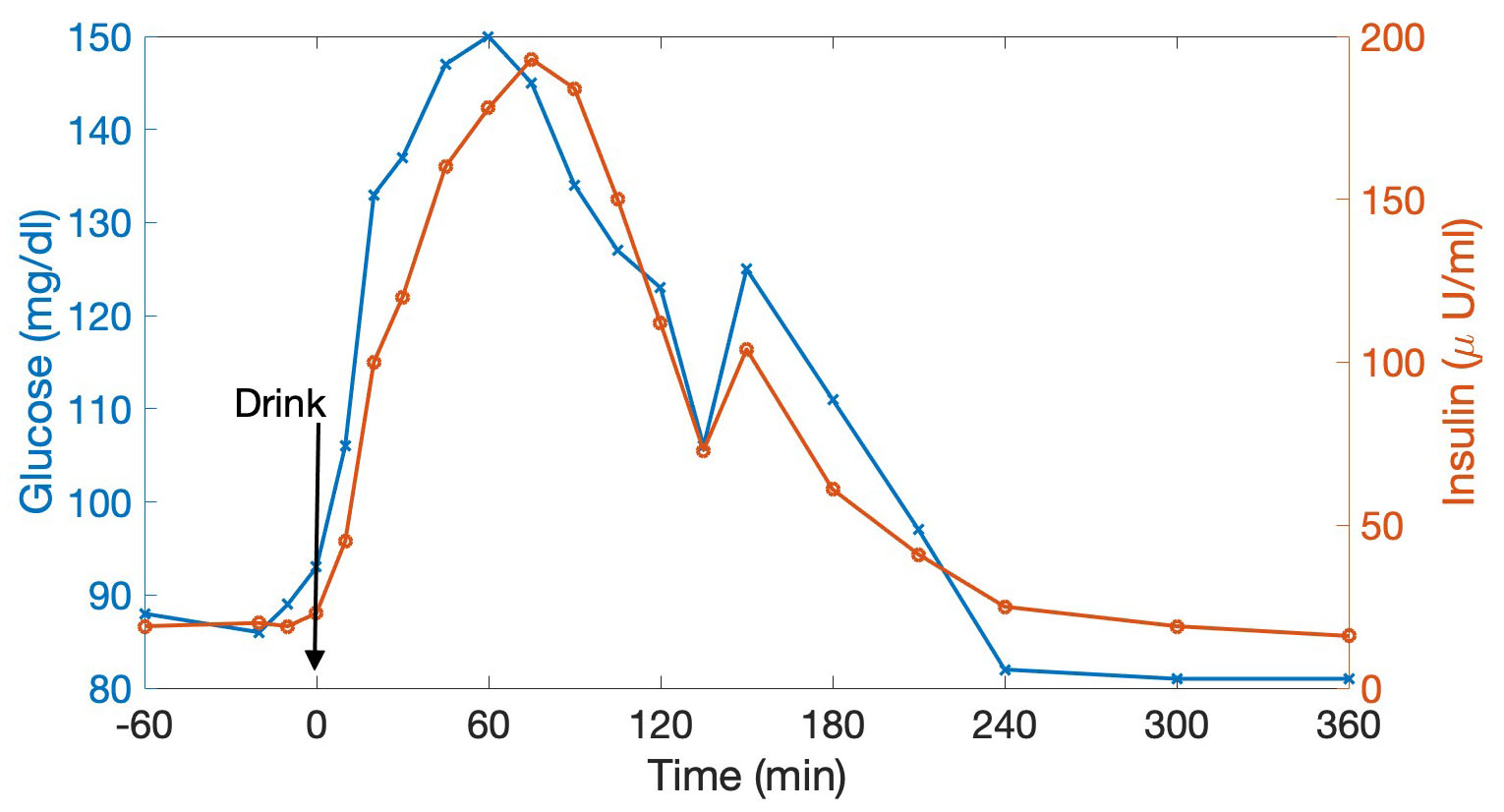
An oral glucose tolerance test (OGTT) yields the most detailed characterization of the dynamical glucose-insulin interactions. During an OGTT, a fasting patient drinks a glucose solution with a predefined amount of glucose. Blood samples are taken at regular time intervals to assess the rise and fall in blood glucose concentrations (see Figure 1). Clinicians use thresholding approaches for blood glucose levels, which are evaluated at one or two-hour time points, to employ OGTTs for high-fidelity diagnoses. Because OGTTs are invasive, physicians use them in limited clinical circumstances — such as for diagnosis of gestational DM, occurrences surrounding bariatric surgery, and instances of cystic fibrosis-related diabetes. More common diagnostic measures include fasting and non-fasting glucose and hemoglobin A1C measurements, which require models and inference approaches that can cope with the lack of insulin data.
To gain additional insight into glucose-insulin dynamics, one can leverage the controlled conditions of an OGTT — as long as they are coupled with inference methods and models that are capable of differentiating mechanisms of metabolic dysregulation. For example, ODE models describe glucose-insulin dynamics and quantify insulin sensitivity based on the profiles of frequently-sampled glucose and insulin concentrations across the OGTT [5, 6]. These models mathematize hypothesized metabolic disruption in individuals and disease states. Inferring their parameters provides a potential pathway for researchers to pinpoint metabolic disruption in individuals and disease states, thereby informing therapeutic interventions, providing personalized treatments, and identifying factors that contribute to disease progression.
In practice, high-fidelity measurements that resemble controlled experiments such as OGTTs are uncommon. As a result, we must cope with sparse, nonstationary, and uncontrolled data. For example, ICU doctors never measure insulin; instead, they measure glucose approximately once an hour to ensure non-unique solutions for exact glycemic trajectories. In addition, they constantly apply interventions that induce non-stationarity and are meant to improve patient health. ICU data are also sparse in time (12 to 24 data points a day) and space (three measured input variables: glucose, nutrition, and medications), thus inducing severe inference and evaluation challenges. Maintaining glucose in the normal range improves patient outcomes, but errors can result in brain starvation, seizures, loss of consciousness, and even death. Doctors therefore attempt to keep blood glucose concentrations slightly high to minimize the probability of downward extremes.
The system that governs glucose-insulin dynamics in the ICU is a time-delayed, nonlinear scheme in which constant infusion of nutrition induces glucose oscillations and instability, including unexpected and dangerously low excursions. The mechanisms that drive glycemic instability in the ICU are poorly understood [9]. Recent work in shear-induced chaos may highlight mechanisms that can create this instability [8]. If one represents glucose-insulin dynamics as a phase space with natural shearing, an external forcing in the form of continuously administered nutrition can cause the space to fold; this phenomenon induces instability in a previously stable system. A series of hard external “kicks” like daily meals may retain a system’s stability, but infrequent kicks—approximated by more or less continuous feeding—can cause the greatest risk. While more work is required to better understand the exact mechanisms of oscillation, the aforementioned approaches provide a language with which to study instability.
Given this variability, it is effort-intensive for medical personnel to manage glucose without the help of computational machinery; even with substantial effort, glycemic goals are difficult to maintain. Personalized endocrine parameter estimation can provide deeper understanding of patient states, and personalized glucose forecasting can maintain more normal glucose levels and produce better outcomes without risking low glucose. Such estimation requires inference machinery to manage the complexities of real-world data by leveraging the knowledge represented in models, data, and clinical expertise to provide accurate physiologic estimation and forecasts.
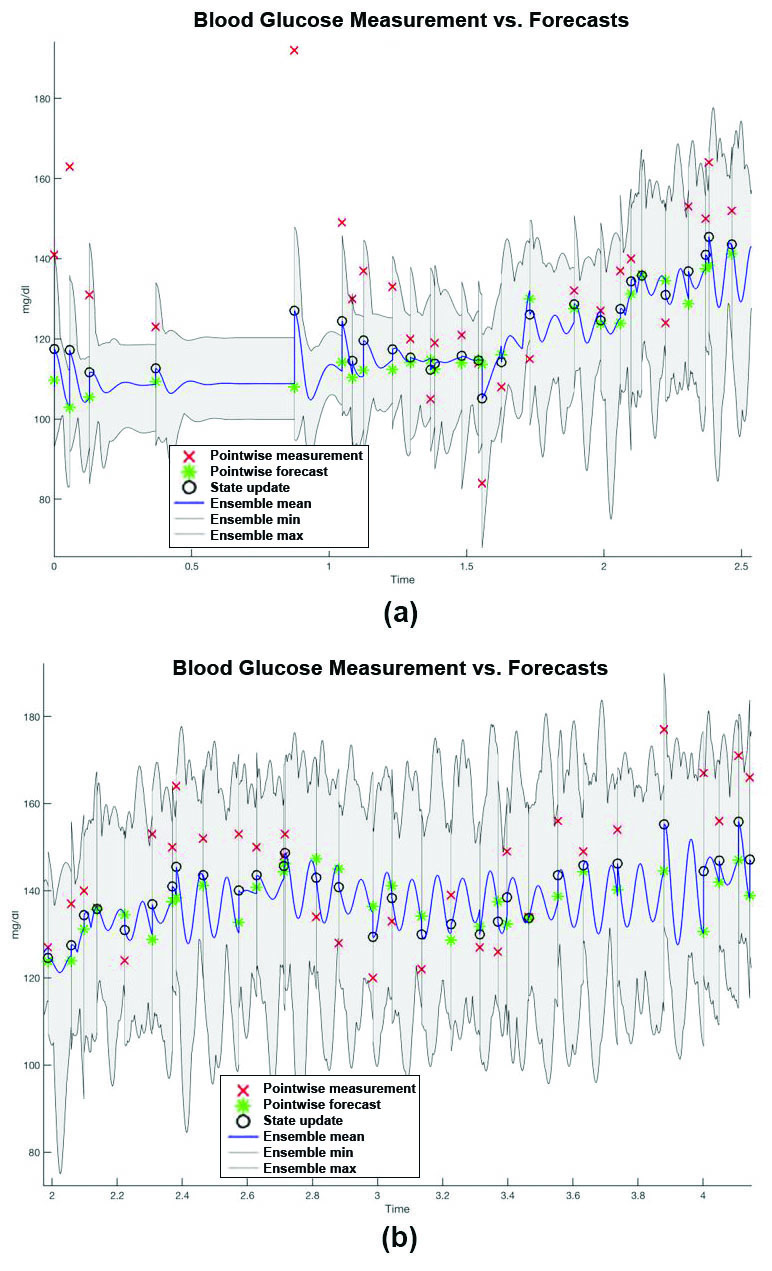
Figure 2 depicts an example of a personalized glucose forecast, which includes the DA model that synchronizes to the patient over the first 1.5 days, followed by continuous tracking over subsequent days. These forecasts yield a quantitative estimate that already represents an advance beyond current capabilities, but they also report the uncertainty surrounding that estimate. This allows us to make informed decisions about our management approaches.
The success of the forecast in Figure 2 should not overshadow the challenges that accompany robust forecasting for all patients. Advances in both models and inference machinery are imperative when facilitating model development and expanding model application in clinical practice. Physiological insights can help refine model structure to better represent the system. However, researchers should focus on developing models that impact decision-making and can be directly probed by external knowledge or clinically collected data. If a detailed physiological representation is not possible in the context of a deterministic model, an alternate approach could involve reducing model fidelity by creating a stochastic model that uses an estimated noise process to represent the poorly-understood or non-inferable physiology [4].
Integrating multiple methods—e.g., implementing a constraint methodology for ensemble Kalman filters (EnKF) [1] and applying machine-learning-based methods to select parameters—reduces identifiability problems and improves inference. For example, the Houlihan method [3] combines machine learning with simulated data to choose effective parameters for estimation, thus reducing the estimation space. One can further reduce this space by integrating clinical and physiologic knowledge into the DA via the introduction of constraints on the filters. Substantial room for innovation exists along this mixed-methodology path of DA and machine learning.
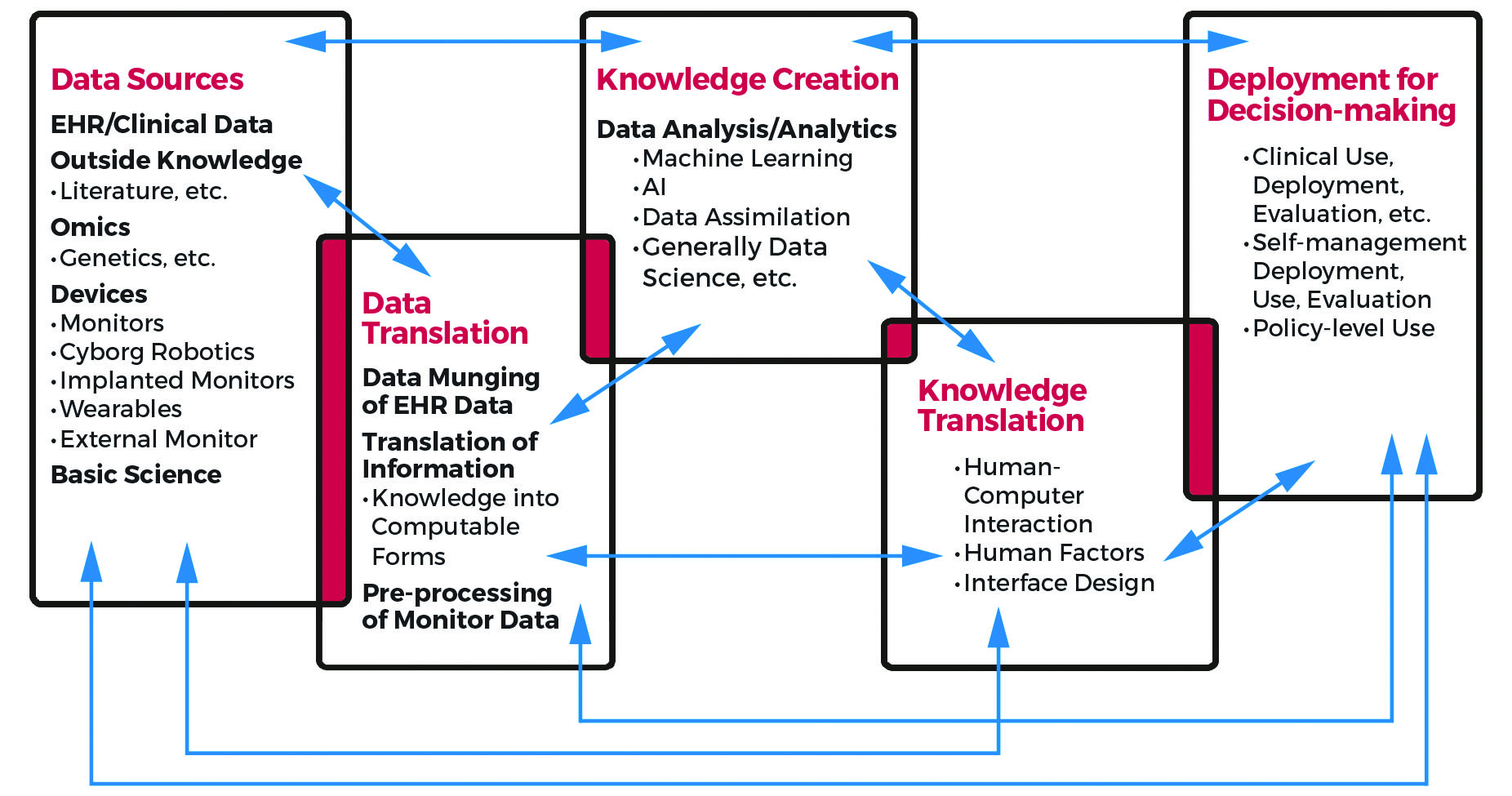
Requirements and limitations of the data and clinical application resulted in a novel method for constraining the EnKF. This method combines EnKF with quadratic programming and requires clinical contributions, physiological input, and mathematical skill. To influence the medical field, mathematical methods must accommodate the reality of sparse, nonstationary data while producing parameter inference and state forecasts that address a recognized need. We must integrate method identification, development, and evaluation—the machinery that facilitates the creation of new data-based knowledge—into an appropriate pipeline (see Figure 3). On the front end, this pipeline should include management of the data sources and translation from operational data into computable data (a complex process in healthcare). On the back end, it must account for translation of the newly created knowledge into a potentially useful form that maximizes end users’ impact.
The ability to provide personalized diagnoses and forecasts will require hybrid approaches that exploit the physiology we do understand, effectively constraining the search space so that each patient’s limited data can yield useful patient-specific results. These mathematical advances, which are necessary to realize precision medicine’s potential, have the capacity to transform the delivery of medicine.
Acknowledgments: We would like to thank Erica Graham, Melike Sirlanci, Joon Ha, William Ott, Bruce Gluckman, Rammah Abohtyra, Kai Bartlette, Matthew Levine, Andrew Stuart, Arthur Sherman, Lena Mamykina, Noemie Elhadad, Tell Bennett, Bhargav Karamched, Jan Claassen, Caroline Der Nigoghossian, and Melanie Cree-Green. We also appreciate funding from NIH-NLM R01 LM012734 and LM006910, as well as NSF-DMS 1853511.
References
[1] Albers, D.J., Blancquart, P.-A., Levine, M.E., Seylabi, E.E., & Stuart, A. (2019). Ensemble Kalman methods with constraints. Inverse Probl., 35(9), 095007.
[2] Albers, D.J., Levine, M., Gluckman, B.J., Ginsberg, H., Hripcsak, G., & Mamykina, L. (2017). Personalized glucose forecasting for type 2 diabetes using data assimilation. PLoS Comput. Biol., 13(4), e1005232.
[3] Albers, D.J., Levine, M.E., Mamykina, L., & Hripcsak, G. (2019). The parameter Houlihan: A solution to high-throughput identifiability indeterminacy for brutally ill-posed problems. Math. Biosci., 316, 108242.
[4] Albers, D.J., Levine, M.E., Sirlanci, M., & Stuart, A.M. (2019). A simple modeling framework for prediction in the human glucose-insulin system. Preprint, arXiv:1910.14193.
[5] Cobelli, C., Dalla Man, C., Toffolo, G., Basu, R., Vella, A., & Rizza, R. (2014). The oral minimal model method. Diabetes, 63(4), 1203-1213.
[6] Ha, J., Satin, L., & Sherman, A. (2015). A mathematical model of the pathogenesis, prevention, and reversal of type 2 diabetes. Endocrinol., 157, 624-635.
[7] Law, K., Stuart, A., & Zygalakis, K. (2015). Data assimilation: A mathematical introduction. New York, NY: Springer.
[8] Ott, W., & Stenlund, M. (2010). From limit cycles to strange attractors. Comm. Math. Phys., 296(1), 215-249.
[9] Pritchard-Bell, A., Clermont, G., Knab, T.D., Maalouf, J., Vilkhovoy, M., & Parker, R.S. (2017). Modeling glucose and subcutaneous insulin dynamics in critical care. Cont. Engineer. Prac., 58, 268-275.
About the Authors
David J. Albers
Associate Professor, University of Colorado
David J. Albers is an informaticist and applied mathematician who develops mathematical machinery to model and understand clinically collected data. He is an associate professor in the Department of Pediatrics, Section of Informatics and Data Science; Department of Biomedical Engineering; and Department of Biostatistics and Informatics at the University of Colorado’s Anschutz Medical Campus. Albers is also an adjunct assistant professor in the Department of Biomedical Informatics at Columbia University Medical Center.

Cecilia Diniz Behn
Associate Professor, Colorado School of Mines
Cecilia Diniz Behn is an applied mathematician focusing on nonlinear dynamics in biological systems. She is an associate professor in the Department of Applied Mathematics and Statistics at Colorado School of Mines. She also holds an appointment as an adjoint assistant professor in the Department of Pediatrics at the University of Colorado School of Medicine.

George Hripcsak
Professor, Columbia University
George Hripcsak is a professor of biomedical informatics and chair of the Department of Biomedical Informatics at Columbia University. He is a board-certified internist with degrees in medicine and biostatistics who focuses on nonlinear time series analysis of electronic health record data and causal inference.

Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



