Digital Twins: Synergy Between Data Assimilation and Optimal Control

In the mid-20th century, John von Neumann envisioned numerical weather prediction as a forthcoming revolutionary application of digital computers. As recounted by theoretical physicist Freeman Dyson, von Neumann delivered a talk at Princeton University in 1950 where he stated that “As soon as we have some large computers working, the problems of meteorology will be solved. All processes that are stable we shall predict. All processes that are unstable we shall control” [2]. This vision has since sown the seeds for the modern concept of numerical weather prediction as a digital twin (DT) of actual weather processes.

Recent advances in computer technology and data acquisition have dramatically expanded von Neumann’s ideas, and DTs in the form of computationally implementable mathematical models of spatiotemporal processes have already found groundbreaking applications in science and engineering. Nevertheless, fundamental mathematical and statistical challenges remain. Here, I will focus on one particular aspect of the DT paradigm: the synergy between data assimilation (DA) and optimal control (OC).

The Data Assimilation and Optimal Control Challenge

A deep integration of DA and OC is essential for the treatment of what von Neumann called the “unstable processes.” But contrary to von Neumann’s notion of the active human control of weather processes, today’s numerical weather prediction systems use observational data from the actual weather to “control” DTs and keep the computational forecasting system close to its physical twin. Modern DA methodologies, such as the ensemble Kalman filter [3], have brought about a paradigmatic change to the prediction of stochastic processes under partial and noisy observations. At the same time, many physical processes do require control—i.e., active interference—in order to meet their desired targets. Such processes occur in aeronautics, chemical engineering, and potentially the mitigation and prevention of extreme weather events.

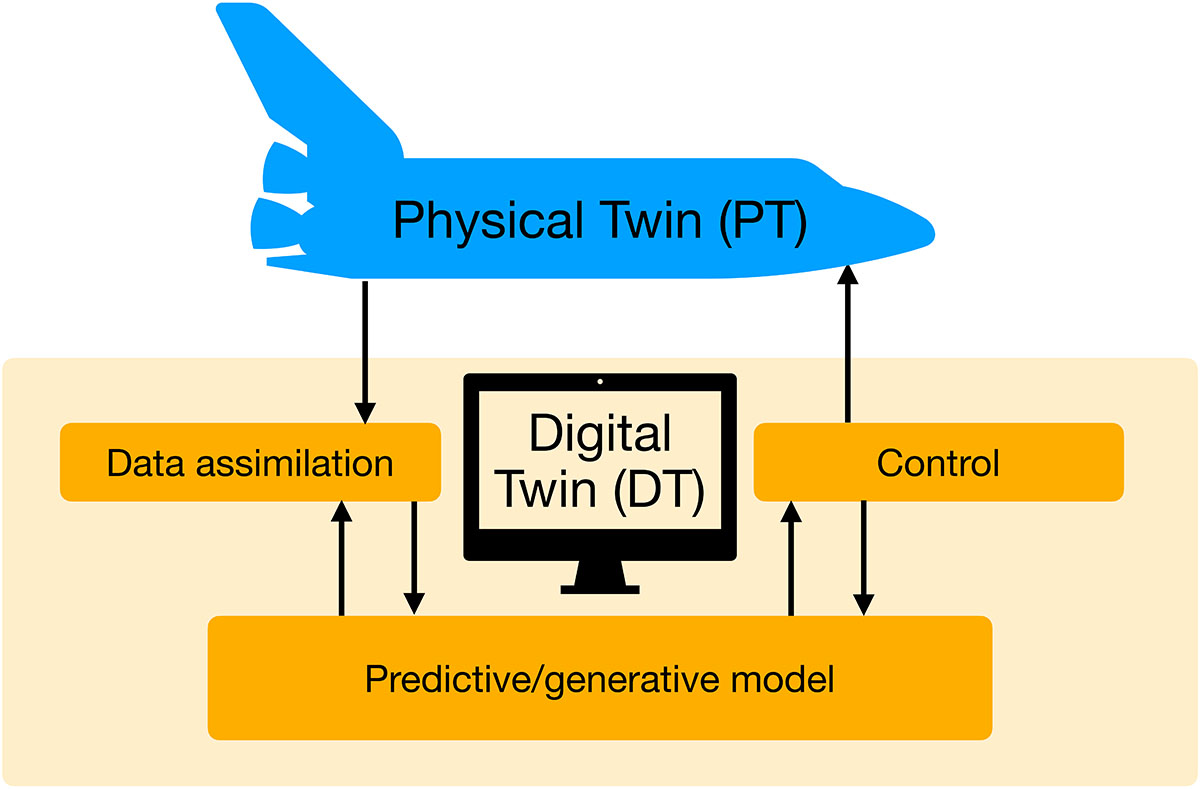
DA has recently seen massive advances in areas like model predictive control and reinforcement learning [6]. However, an outstanding computational challenge involves its combination with OC to enable the real-time control and prediction of partially observed physical processes (see Figure 1) [4]. Most modern control algorithms assume a complete knowledge of model states, whereas DA techniques are applied to uncontrolled processes. When combining OC with DA for partially observed processes, the feedback control laws depend on forecast distributions instead of model states, and the forecast distributions in turn depend on these control laws. Essentially, the situation necessitates a deeper integration of DA and OC.

Novel Approaches to Data Assimilation and Optimal Control

Beginning with the work of Rudolf Kálmán, a strong link has long existed between estimation and control; the well-established field of partially observed Markov decision processes also provides important background [6]. However, DTs of complex, high-dimensional processes—such as numerical weather prediction—require a fundamental reconsideration of the interplay between DA and OC. I will illustrate this point with two examples and outline a mathematical framework in terms of the McKean stochastic evolution equations.

As its name suggests, DA is typically understood as a sequential algorithm that alternates between the prediction and assimilation of data. This type of split can lead to difficulties whenever the forecast is far from the data, as with extreme weather events. In principle, we can mathematically fix this issue by reformulating the combined prediction and assimilation task as a Schrödinger bridge mean field control problem [9]. But because this observation does not directly deliver implementable algorithms, we must find alternative McKean control laws that (i) are easier to compute and (ii) do not explicitly rely on knowledge of the posterior target distribution, but (iii) still couple the desired distributions. One possible solution uses a generative model in \(X_t\) in the form of a stochastic differential equation (SDE):

\[{\rm d}X_t = b(X_t){\rm d}t + \sigma{\rm d}B_t, \tag1\]

where \(B_t\) denotes standard Brownian motion [10]. Given observational data \(Y_{t_n}^\dagger\) at discrete times \(t_n = n\Delta t\), \(n\ge 1\), we define appropriate mean field control laws \(u_t(x,\hat \mu_t)\) so that the resulting McKean SDE

\[{\rm d}\hat X_t = b(\hat X_t){\rm d}t + u_t(\hat X_t,\hat \mu_t){\rm d}t + \sigma {\rm d}B_t \tag2\]

approximates the desired posterior distributions at observation times \(t=t_n\). Here, \(\hat \mu_t\) represents the law of \(\hat X_t\). This example demonstrates control theory’s ability to guide DA and enable better predictions.

At the other end of the spectrum, researchers have recently begun to reformulate control problems in terms of forward and reverse-time McKean SDEs by replacing the Hamilton-Jacobi-Bellman equation with the value function \(y_t(x)\). We can thus express the gradient of the value function as \(\nabla_x y_t(x) = \nabla_x \log \mu_t^+(x) - \nabla_x \log \mu_t^-(x)\), where \(\mu_t^+\) denotes the law of an appropriate forward McKean SDE and \(\mu_t^-\) denotes the law of a reverse-time McKean SDE. A DA-based implementation of this approach exemplifies DA’s capacity to help solve control problems [5]. We can also extend the technique to more general OC problems, and a very closely related methodology comprises the heart of diffusion-based generative modeling [11].

But to integrate DA and OC in the context of partially observed and controlled processes, we need another level of DA and OC synergy that utilizes a common mathematical and algorithmic foundation based on random probability measures and their time evolution. Building upon the tremendous success of the ensemble Kalman filter, a promising direction involves the formulation of McKean stochastic evolution equations for both DA and OC to ultimately create online adaptations of DTs and optimally control their physical twins. So, let us replace \((1)\) with the controlled SDE

\[{\rm d}X_t = b(X_t,U_t){\rm d}t + \sigma B_t, \tag3\]

where \(U_t\) signifies the control. To simplify, we now assume continuous observations according to the forward model

\[{\rm d}Y_t = h(X_t){\rm d}t + {\rm d} W_t,\]

where \(W_t\) indicates Brownian motion that is independent of \(B_t\). If we express an actual observation as \(Y_t^\dagger\), \(t\ge 0\), then a McKean formulation of the continuous-time ensemble Kalman-Bucy filter is given by

\[\begin{eqnarray} {\rm d}\tilde X_t &=& b(\tilde X_t,U_t){\rm d}t + \sigma {\rm d}B_t + K(\tilde \mu_t)({\rm d}Y_t^\dagger - {\rm d}\tilde Y_t ), \\ {\rm d}\tilde Y_t &=& h(\tilde X_t){\rm d}t + {\rm d}W_t. \end{eqnarray} \tag4\]

This formulation adds a data-driven control term to the generative model in \((3)\); we can draw a comparison with \((2)\) for discrete-time observations.

The so-called Kalman gain \(K(\tilde \mu_t)\) depends on the law \(\tilde \mu_t\) of \(\tilde X_t\) [1]. Let us further assume that the desired control is of the form \(U_t = u_\beta(\tilde \mu_t)\)—where \(\beta\) is a set of parameters—and that the optimal parameter choice \(\beta_\ast\) minimizes the time-averaged cost functional

\[J(\beta) = \lim_{T\to \infty}\frac{1}{T} \int_0^T \tilde \mu_t \left[c(\cdot,u_\beta(\tilde \mu_t))\right] {\rm d}t. \tag5\]

Here, \(c(x,u)\) is some appropriate running cost and \(\tilde \mu_t[c(\cdot,U_t)]\) is its expectation value under \(\tilde \mu_t\). Invoking ergodicity, the computation of \((5)\) reduces to an expectation value with respect to an equilibrium distribution of random probability measures that depends on \(\beta\). A proposed algorithmic approach applies derivative-free and affine invariant DA-based minimization methods to compute the desired parameter \(\beta\) in tandem with \((4)\) [1]. In other words, the McKean stochastic evolution equations in time-dependent parameters \(\beta_t\) should augment \((4)\) such that \(\lim_{t\to \infty}\beta_t = \beta_\ast\).

McKean formulations in \((\tilde X_t,\beta_t)\) must play (at least) two roles: (i) Giving rise to efficient online algorithms and (ii) allowing for uncertainty quantification from a frequentist perspective. Both of these tasks are difficult because the relevant probability measures are random and time dependent.

Challenges and Opportunities

Most DA research thus far has been based on the assumption of ideal twins, which presumes that the physical twin and DT are mathematically identical — an unrealistic premise for real-world applications. The robustness of DA and OC algorithms enables them to model discrepancies and thus constitutes an extremely important research direction. For instance, one recent study adapted stochastic gradient descent for robust parameter estimation from multiscale data [7].

Data-driven DTs that utilize generative machine learning models are set to bring another paradigmatic change to the field. The novel GenCast weather prediction model from Google DeepMind [8] is the first generative model to deliver ensemble predictions at a much higher speed than conventional models. Such data-driven forecasting models could hence allow for much larger ensemble sizes—compared to the current scale of \({\rm O}(100)\)—and significantly more accurate DA methodologies. These models rely on reanalysis data and are therefore limited to past weather incidents, which raises questions about the statistical accuracy of their predictions of future events. Alternatively, could we make online adjustments to generative DTs to account for new partial and noisy data?

DTs offer numerous exciting research pursuits at the intersection of DA, OC, and generative modeling. Several upcoming sessions will provide opportunities to get involved in this field, including a long program on “Digital Twins: Mathematical and Statistical Foundations and Complex Applications” at the Institute for Mathematical and Statistical Innovation this fall and a workshop on the “Mathematical Foundation of Digital Twins” at the Oberwolfach Research Institute for Mathematics in June 2026. Returning to von Neumann’s vision, Goal 8 of the Japan Science and Technology Agency’s Moonshot Research and Development Program seeks to devise weather control technology that is socially, technically, and economically feasible. Achieving these goals will require significant advances that build upon the synergy of DA and OC.

Acknowledgments: This work is partially funded by the Deutsche Forschungsgemeinschaft, Project-ID 318763901 - SFB1294.

References
[1] Calvello, E., Reich, S., & Stuart, A.M. (2025). Ensemble Kalman methods: A mean field perspective. Acta Numer. To be published.
[2] Dyson, F. (1988). Infinite in all directions. New York, NY: Harper & Row.
[3] Evensen, G., Vossepoel, F.C., & van Leeuwen, P.J. (2022). Data assimilation fundamentals: A unified formulation of the state and parameter estimation problem. Cham, Switzerland: Springer Nature.
[4] Kapteyn, M.G., & Willcox, K.E. (2021, September 1). Digital twins: Where data, mathematics, models, and decisions collide. SIAM News, 54(7), p. 1.
[5] Maoutsa, D., & Opper, M. (2022). Deterministic particle flows for constraining stochastic nonlinear systems. Phys. Rev. Res., 4(4), 043035.
[6] Meyn, S. (2022). Control systems and reinforcement learning. Cambridge, U.K.: Cambridge University Press.
[7] Pavliotis, G.A., Reich, S., & Zanoni, A. (2025). Filtered data based estimators for stochastic processes driven by colored noise. Stoch. Process. Appl., 181(3), 104558.
[8] Price, I., Sanchez-Gonzalez, A., Alet, F., Andersson, T.R., El-Kadi, A., Masters, D., … Willson, M. (2025). Probabilistic weather forecasting with machine learning. Nature, 637(8044), 84-90.
[9] Reich, S. (2019). Data assimilation: The Schrödinger perspective. Acta Numer., 28, 635-711.
[10] Reich, S. (2024). Data assimilation: A dynamic homotopy-based coupling approach. In B. Chapron, D. Crisan, D. Holm, E. Mémin, & A. Radomska (Eds.), Stochastic transport in upper ocean dynamics II (STUOD 2022 workshop) (pp. 261-280). Mathematics of planet Earth (Vol. 11). London, U.K.: Springer Nature.
[11] Reich, S. (2025). Particle-based algorithm for stochastic optimal control. In B. Chapron, D. Crisan, D.D. Holm, E. Mémin, & J.-L. Coughlan (Eds.), Stochastic transport in upper ocean dynamics III (STUOD 2023 workshop) (pp. 243-267). Mathematics of planet Earth (Vol. 13). Plouzané, France: Springer Nature.