Discrete Curvature and Applications in Graph Machine Learning

Graph-structured data is ubiquitous in machine learning and data science applications, including biochemistry, drug discovery, social networks, and the design of new materials. To find success in such settings, graph learning methods must often leverage intrinsic data structures and their geometric characterizations.

Discrete notions of curvature can help characterize the geometric properties of graph-structured data. Curvature is a central concept in differential geometry that describes the geometric properties of geodesic spaces. On smooth manifolds, Ricci curvature characterizes local volume growth and geodesic dispersion. In graph learning, however, the data space is inherently discrete and there is no natural differential structure based on which curvature can be defined.

To mitigate this issue, researchers have extended some classical notions of curvature, including Ricci curvature, to discrete spaces via curvature analogies. Here, we introduce two such notions—Ollivier-Ricci [9] and Forman-Ricci curvature [5]—and describe their utility when analyzing both local and global geometric properties of graph-structured data. We then discuss curvature-based methods for graph machine learning that exploit such geometric characterizations, including “shallow” methods like community detection [8, 10, 11] and “deep” learning on graphs via graph neural networks [2-4, 12].

Notions of Discrete Curvature

The lack of a natural differential structure presents a fundamental challenge when defining notions of curvature in discrete spaces. We can overcome this difficulty by defining discrete curvatures via curvature analogies: In continuous settings, curvature relates to several other classical geometric tools, many of which have well-studied discrete counterparts. By defining curvatures that preserve these relations in discrete settings, we obtain notions that retain key geometric features of their continuous counterparts — thus enabling rigorous analysis of local and global geometric structures in discrete settings.

Ollivier-Ricci Curvature

Yann Ollivier introduced a notion of Ricci curvature that relates the curvature along a geodesic between nearby points on a manifold to the optimal transportation distance between their respective neighborhoods [9]. This approach relies on the close connection between the behavior of random walks that are initiated at nearby points—characterized by optimal transport—and the manifold’s Ricci curvature. In particular, random walks are likely to converge if the Ricci curvature is positive and diverge if it is negative.

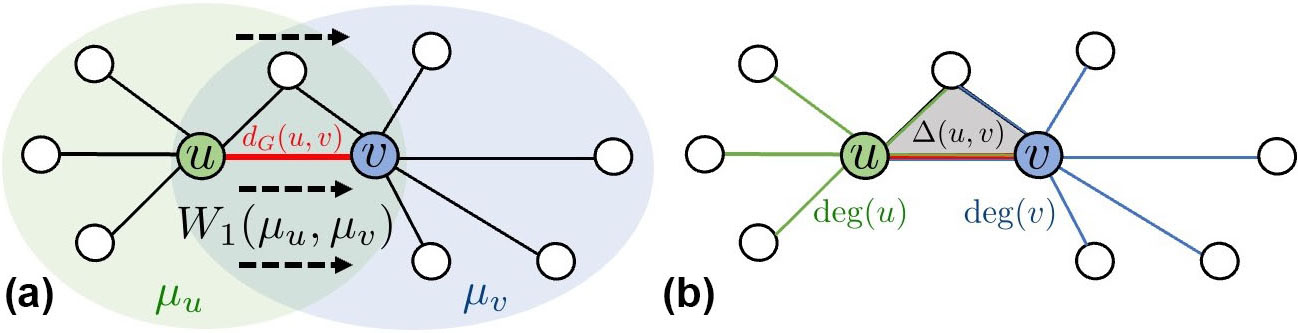
This idea naturally extends to graphs, where random walks are well studied. If uniform random walks are initiated at neighboring nodes \(u\) and \(v\), they will likely remain close if the neighborhoods of \(u\) and \(v\) overlap significantly and draw apart if there is little overlap. We may quantify this phenomenon by using the Wasserstein-1 distance \(W_1(\mu_u, \mu_v)\) between measures \(\mu_u\) and \(\mu_v\), which are induced by random walks initiated at \(u\) and \(v\) (see Figure 1a). Accordingly, we can define the following notion of curvature, which is positive when the random walks stay close and negative when they drift apart:

\[\kappa(u,v)=1-\frac{W_1(\mu_u,\mu_v)}{d_G(u,v)}.\]

Here, \(d_G(u,v)\) denotes the shortest path distance. To compute the Ollivier-Ricci curvature, we must solve an optimal transport problem for each edge in the graph. In the worst case, this procedure has a complexity of \(O(|E| \, m^3)\), where \(|E|\) is the number of edges and \(m\) denotes the maximum degree of nodes in \(G\). Faster approximations with Sinkhorn distances or combinatorial approximations can significantly reduce the complexity [11].

Forman-Ricci Curvature

Robin Forman introduced a discrete notion of Ricci curvature based on a discrete analogue of the Bochner-Weitzenböck identity, a fundamental relationship between Ricci curvature and Laplacians in the continuous setting [5]. In the special case of unweighted graphs, the Forman-Ricci curvature is defined as follows:

\[\textrm{Ric}_F(u,v)=4-\textrm{deg}(u)-\textrm{deg}(v)+3\triangle(u,v)+2\square(u,v)+....\]

Here, \(\triangle(u,v)\) and \(\square(u,v)\) denote the number of triangles and quadrangles that contain the edge \((u,v)\) (see Figure 1b). Higher-order terms that correspond to \(k\)-cycles (where \(k>4\)) are usually omitted. The computational complexity of Forman’s curvature is smaller than that of Ollivier’s. If we only include the curvature contributions of 3-cycles—which is often sufficient in practice—we obtain a complexity of \(O(|E| \, m)\).

Relation to Classical Ricci Curvature

Continuum limits provide a natural bridge between discrete and continuous settings in graphs. Geometric graphs, which are often constructed from \(\epsilon\)-nets of point clouds (i.e., connections of nodes within distance \(\epsilon\)), capture the spatial structure of the underlying data. As the number of nodes—and hence the resolution of the geometric graph—increases, continuum limits reveal the graph’s intrinsic geometry.

Recent literature has leveraged the lens of continuum limits to examine the relationship between discrete and continuous Ricci curvature. A 2021 study established the first asymptotic convergence result for Ollivier-Ricci curvature [14]. Several years later, researchers provided more refined non-asymptotic error bounds in the finite sample regime and showed that the Ollivier-Ricci curvature of a geometric graph allows one to infer global bounds on the Ricci curvature of the manifold from which it was sampled [13]. These convergence results do not rely on access to true geodesic distances; they also hold for data-driven approximations thereof.

Applications in Shallow Graph Learning

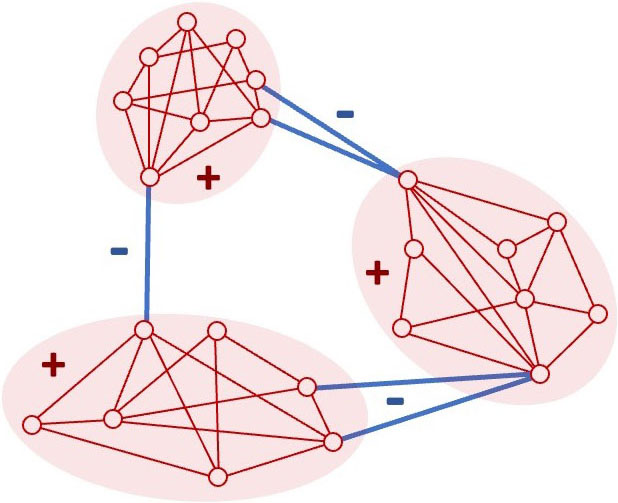
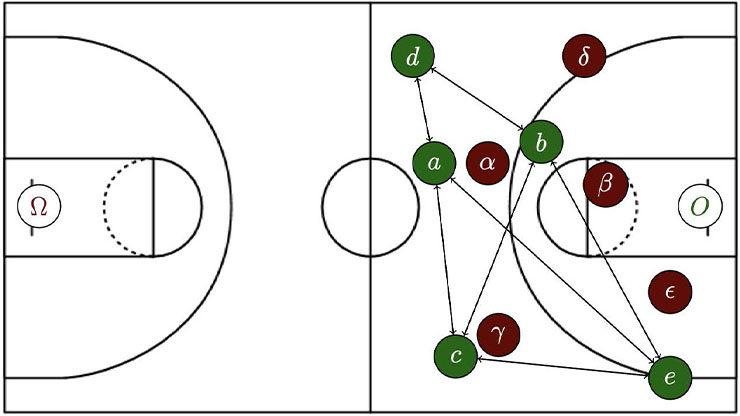
Curvature-based Clustering: Community detection, also known as unsupervised node clustering, seeks to identify densely connected substructures that are comprised of “similar” nodes in a graph. Classical algorithms for community detection include spectral clustering and the Louvain method, though newer studies have leveraged discrete Ricci curvature and associated geometric flows [8, 10, 11]. These approaches exploit the observation that edges between communities tend to have low curvature, while edges within communities have high curvature (see Figure 2). Curvature-based thresholding removes low-curvature edges, revealing community structure through the remaining connected components; an associated discrete Ricci flow can further refine the detection. While initial methods focused on single-membership community detection, recent work has since extended curvature-based techniques to mixed-membership settings by applying them to the line graph—i.e., the graph’s dual—to better capture the geometry of overlapping communities [11].

Curvature-based Coarsening: Graph coarsening reduces a graph’s size while preserving its key structural properties, typically by merging nodes via edge contraction. From a discrete curvature perspective, edges with high curvature are prime candidates because they represent connections of low structural importance, thus motivating the development of curvature-based pooling operators and coarsening techniques [2, 15]. Graph coarsening has applications in exploratory data analysis, data visualization, and the simplification of large graphs to facilitate more computationally intensive downstream analyses.

Applications in Deep Graph Learning

Graph neural networks (GNNs) are a popular type of architecture for deep learning on graphs. Many GNNs are based on the message-passing paradigm, which iteratively computes node embeddings by combining structural information (from the graph’s adjacency) with features (encoded in node attributes) [6]. At each layer, nodes aggregate “messages” from their neighbors and use a trainable function to update their embeddings.

Over-smoothing and Over-squashing: Over-squashing [1] describes the compression of long-range information through bottlenecks in message-passing, while over-smoothing [7] characterizes a collapse of node representations in deeper networks. Geometrically, edges that introduce bottlenecks have low curvature [12], whereas dense regions—which are characterized by high curvature—are prone to over-smoothing. Discrete curvature thus provides a framework to analyze both effects. Graph rewiring techniques perturb the input graph by removing edges in high-curvature regions to combat over-smoothing and adding edges in low-curvature regions to alleviate over-squashing [3, 12]. The curvature gap, a global characteristic of the curvature distribution, can help determine suitable curvature thresholds for edge perturbation [3].

Geometric Augmentation: The limited representational power of GNNs presents further challenges. We may wonder what functions GNNs can learn, which is equivalent to asking whether they map topologically identical graphs to the same representation. Standard message-passing GNNs fail this test for many classes of graphs—including regular graphs [16]—which limits their ability to compute basic properties, such as the graph’s diameter or the size of its largest cycle. More powerful architectures, like higher-order GNNs and topology-aware message-passing that encode local substructures, may address these issues but are often less computationally efficient. A simpler solution is to augment the input graph with geometric information that the GNN could not learn on its own. Researchers have proposed various augmentations—known as encodings—that leverage graph characteristics, such as the spectrum of the graph Laplacian, substructure counts, and discrete curvature [4]. Curvature captures structural information over a node’s two-hop neighborhood, in contrast to the one-hop view of standard message-passing. This augmentation is both effective—often outperforming other encodings—and scalable, since the curvature notion’s locality allows for parallelization of its computation.

Melanie Weber delivered a minisymposium presentation about this research at the 2024 SIAM Conference on Mathematics of Data Science, which took place in Atlanta, Ga., last October.

Acknowledgments: The author is supported by U.S. National Science Foundation awards CBET-2112085 and DMS-2406905, as well as a Sloan Research Fellowship in Mathematics.

References
[1] Alon, U., & Yahav, E. (2021). On the bottleneck of graph neural networks and its practical implications. In International conference on learning representations (ICLR 2021).
[2] Feng, A., & Weber, M. (2024). Graph pooling via Ricci flow. Trans. Mach. Learn. Res.
[3] Fesser, L., & Weber, M. (2023). Mitigating over-smoothing and over-squashing using augmentations of Forman-Ricci curvature. In Proceedings of the second learning on graphs conference (LoG 2023). Proceedings of Machine Learning Research.
[4] Fesser, L., & Weber, M. (2024). Effective structural encodings via local curvature profiles. In International conference on learning representations (ICLR 2024). Vienna, Austria.
[5] Forman, R. (2003). Bochner’s method for cell complexes and combinatorial Ricci curvature. Discrete Comput. Geom., 29(3), 323-374.
[6] Gori, M., Monfardini, G., & Scarselli, F. (2005). A new model for learning in graph domains. In Proceedings of the 2005 IEEE international joint conference on neural networks (pp. 729-734). Montreal, Canada: Institute of Electrical and Electronics Engineers.
[7] Li, Q., Han, Z., & Wu, X.-M. (2018). Deeper insights into graph convolutional networks for semi-supervised learning. In Proceedings of the thirty-second AAAI conference on artificial intelligence (pp. 3538-3545). New Orleans, LA: Association for the Advancement of Artificial Intelligence.
[8] Ni, C.-C., Lin, Y.-Y., Luo, F., & Gao, J. (2019). Community detection on networks with Ricci flow. Sci. Rep., 9, 9984.
[9] Ollivier, Y. (2010). A survey of Ricci curvature for metric spaces and Markov chains. Adv. Stud. Pure Math., 57, 343-381.
[10] Sia, J., Jonckheere, E., & Bogdan, P. (2019). Ollivier-Ricci curvature-based method to community detection in complex networks. Sci. Rep., 9, 9800.
[11] Tian, Y., Lubberts, Z., & Weber, M. (2025). Curvature-based clustering on graphs. J. Mach. Learn. Res., 26, 1-67.
[12] Topping, J., Di Giovanni, F., Chamberlain, B.P., Dong, X., & Bronstein, M.M. (2022). Understanding over-squashing and bottlenecks on graphs via curvature. In International conference on learning representations (ICLR 2022).
[13] Trillos, N.G., & Weber, M. (2023). Continuum limits of Ollivier’s Ricci curvature on data clouds: Pointwise consistency and global lower bounds. Preprint, arXiv:2307.02378.
[14] Van der Hoorn, P., Cunningham, W.J., Lippner, G., Trugenberger, C., & Krioukov, D. (2021). Ollivier-Ricci curvature convergence in random geometric graphs. Phys. Rev. Res., 3, 013211.
[15] Weber, M., Saucan, E., & Jost, J. (2017). Characterizing complex networks with Forman-Ricci curvature and associated geometric flows. J. Complex Netw., 5(4), 527-550.
[16] Xu, K., Hu, W., Leskovec, J., & Jegelka, S. (2019). How powerful are graph neural networks? In International conference on learning representations (ICLR 2019). New Orleans, LA.