Dynamics of Droplet Formation and Pinch-off with a One-dimensional Mathematical Model
Droplets arise in a wide variety of applications, from emulsion and spraying to ink-jet printing and even atomization for rocket engines [4]. A deep understanding of droplet dynamics is crucial to improving the efficacy of these operations. While it may appear ordinary to the naked eye, the droplet formation process is full of physics and intricate mathematics that describe the governing method of droplet pinch-off. Almost all applications of droplet generation require control of certain quantities of interest for the separated droplet, such as volume, frequency of droplet generation, surface area, and average moving velocity.
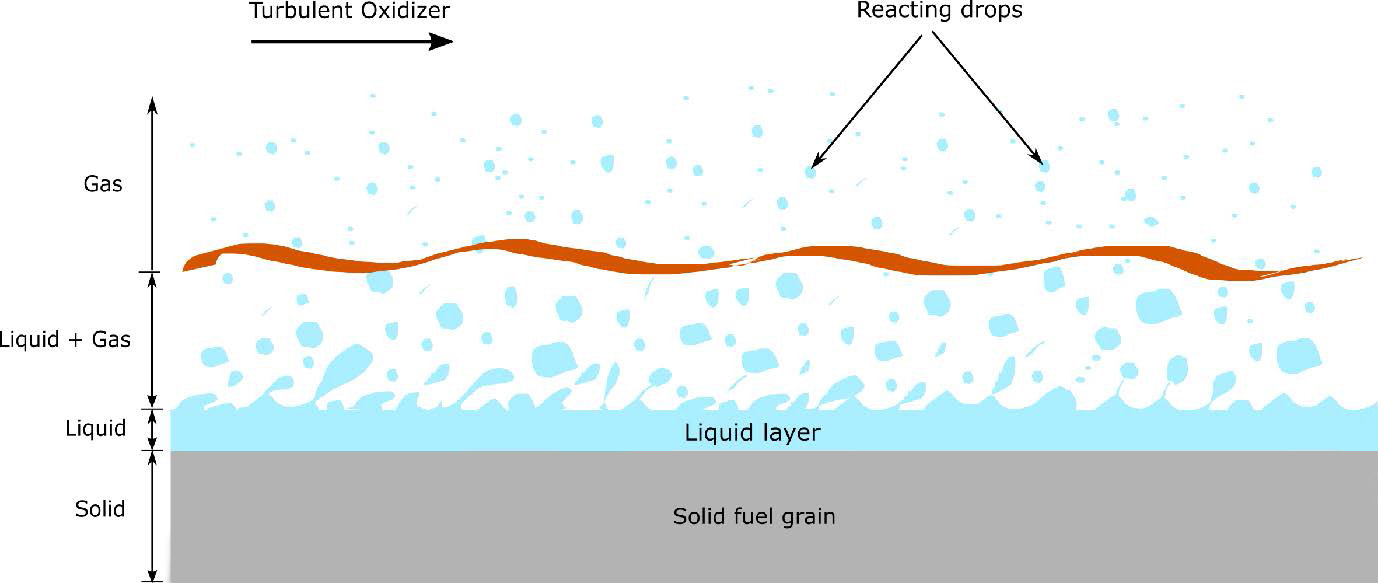
Atomization processes convert bulk liquid into a dispersion of smaller droplets and thus rely on droplet formation and pinch-off. These processes comprise the heart of the novel space technology of hybrid rockets, which—in contrast to purely liquid-fueled engines—run on fuels that are environmentally friendly, abundant, and easy to handle and store. Paraffin wax is a prominent candidate among the possible high-regression-rate fuels for hybrid rocket engines [5]. Within these engines, high-temperature oxidizer gas flow causes the solid fuel grain to melt and creates a liquid layer (see Figure 1). This liquid layer becomes unstable due to the shearing effect of the fast-moving gas — an example of Kelvin-Helmholtz instability. The instabilities grow and lead to the creation of droplets, which pinch off and react with the combustion gases to produce thrust. Knowing both the volume of these droplets and the required pinch-off time is essential to the accurate prediction of fuel regression and rocket thrust
To gain insight into the basics of the droplet formation process, let us look at the example of a pendant droplet under gravity. Initially, a fluid column is situated at the outlet of a nozzle. The addition of more fluid causes the column to become heavier, and the influence of gravity begins to elongate the structure. Meanwhile, surface tension works to minimize the surface energy by changing the surface curvature; this effect creates a neck with a rapidly decreasing radius. The radius of this fluid column eventually goes to zero, and the droplet separates from the original fluid. In 1993, Jens Eggers established the mathematical foundation for this process by creating a scaling solution of the axisymmetric fluid neck that appears during droplet breakup [2]. One year later, Eggers and Todd Dupont used the asymptotic expansion of the Navier-Stokes equations to develop a one-dimensional (1D) mathematical model [3]. Inspired by this work, we utilized a mixed finite element formulation and self-consistent determination of droplet length to construct a 1D model that simulates droplet pinch-off in a quiescent environment with accurate curvature [6]. The model equations are as follows:
\[\frac{\partial h}{\partial t}+u\frac{\partial h}{\partial z} + \frac{h}{2}\frac{\partial u}{\partial z}=0\tag1\]
\[\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial z}+ \frac{\gamma}{\rho}\frac{\partial \mathcal{K}}{\partial z} - \frac{6\nu}{h}\frac{\partial u}{\partial z}\frac{\partial h}{\partial z}-3\nu\frac{\partial^2u}{\partial z^2}-g=0,\tag2\]
where \(\mathcal{K}\) represents the full curvature and is given by
\[\mathcal{K}=\Bigg[\frac{1}{h\big(1+\frac{\partial h}{\partial z}^2\big)^{1/2}}- \frac{\frac{\partial^2 h}{\partial z^2}}{\big(1+\frac{\partial h}{\partial z}^2\big)^{3/2}}\Bigg].\tag3\]
Solving these equations with a mixed finite element approach accurately captures the curvature. We then employ adaptive mesh refinement, conservative Galerkin projection between moving meshes, and a self-consistent algorithm to compute droplet length. The implementation makes use of the Portable, Extensible Toolkit for Scientific Computation (PETSc) library [1].
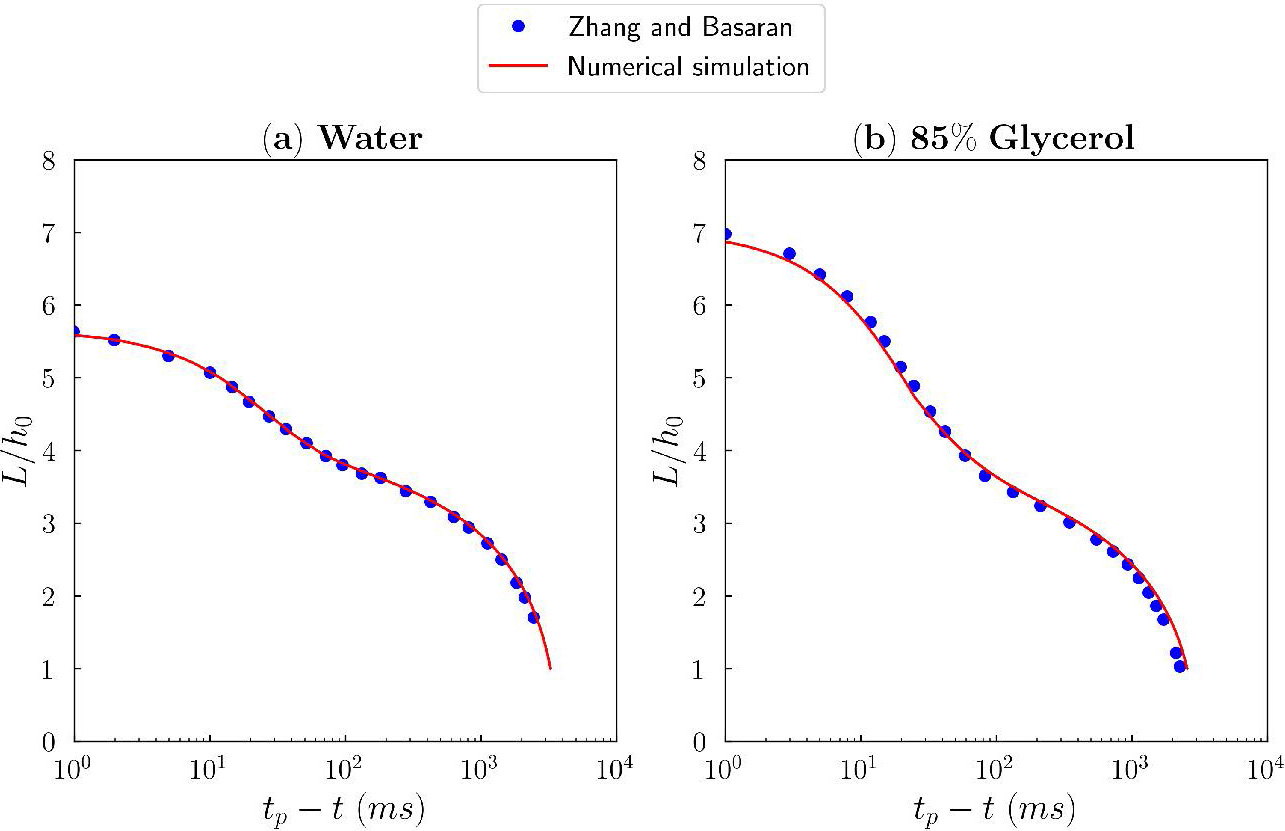
We verified the model via the method of manufactured solutions and validated it against laboratory experiments [7]. Figure 2 provides the numerical simulation results along with experimental data for both water and an 85 percent glycerol solution. The y-axis represents a droplet length \((L)\) that is non-dimensionalized by the inlet radius \((h_0)\), and the x-axis represents the time distance from the pinch-off. The comparison between experimental and simulation results suggests that our 1D model accurately captures the evolution of the droplet interface and predicts the experimental droplet sizes and pinch-off times. Moreover, the difference in droplet evolution indicates the importance of the viscous forces during the pinch-off process. Highly viscous fluids—such as glycerol—exhibit elongated neck structures when compared to low-viscosity fluids like water under the same inflow conditions. The droplet profiles in Figure 2 for the last few points of both cases illustrate this finding.
To predict the droplet sizes for hybrid rocket atomization, we performed the simulations for liquid paraffin wax at various inlet radii. These simulations serve as a basis for analysis, so it is useful to include all possible initial conditions that may arise prior to Kelvin-Helmholtz instability. Figure 3 shows a sequence of droplet images at the time of pinch-off for varying inlet radii, ranging from 0.4 millimeters to 4 millimeters with an increment of 0.4 millimeters. An increasing inlet radius results in slightly bigger droplets. However, the primary droplet’s shape varies significantly with changes in inlet radii. Due to differences in the duration of the necking process, the primary droplet evolves from a vertical ellipsoid to a sphere and then to a horizontal ellipsoid as inlet radius increases.
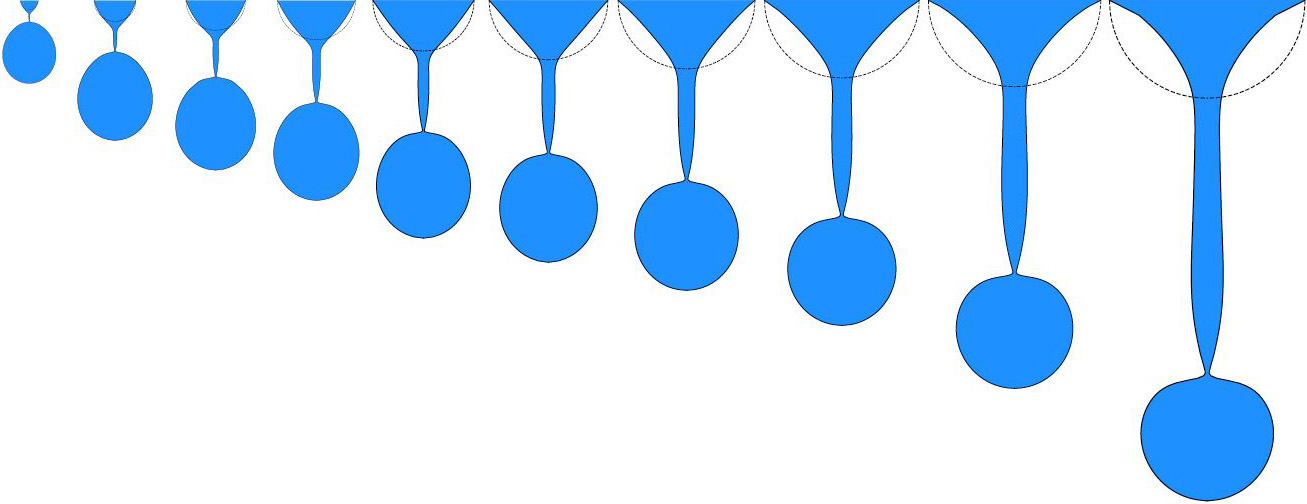
The smaller inlet radii cases spend more time in the radial growth phase as they wait for sufficient fluid so that gravity can compete with surface tension; these cases then take less time during necking due to the lower surface energy. However, this trend begins to switch as we enlarge the inlet radius. For larger inlet radii, necking takes comparatively more time because of the larger surface energy, but radial growth takes almost no time since the initial droplet is large enough for gravity to start acting immediately to overcome surface tension. This transition yields a sweet spot for the pinch-off time, which increases, reaches a peak, and then begins to decrease as the inlet radius grows. When the primary droplet finally separates, the neck recoils with high velocity; the recoiling motion perturbs the neck and stimulates its breakup into a sequence of smaller droplets called satellite droplets. A longer neck, as occurs for larger inlet radii, therefore creates an opportunity for secondary droplet formation — a crucial process for accurate prediction of atomized droplet volume.
In these simulations, gravity serves as the external force. However, the atomization process actually occurs due to both gravity and shear forcing. Researchers typically use two-dimensional simulations to study shear-induced droplet formation, but the droplet evolution shows rotational symmetry and can be modeled with a 1D approach (as in the gravitational case).
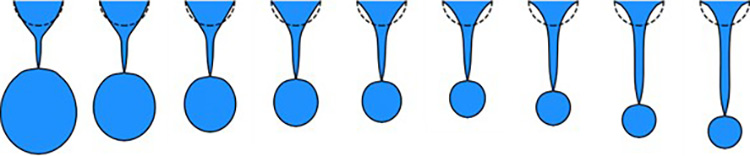
We have developed a 1D model that includes the shear effects of the outer flow on droplet evolution, and are currently producing surrogate models for paraffin droplet production in hybrid rocket engines. Figure 4 displays a series of droplet formation images for various outer flow velocities. The change in outer velocity alters the shear force on the droplet interface: a higher outer velocity exerts more shear force, which extends the fluid column at a faster rate and forces the droplet to pinch off. We plan to extend this model to simulate the secondary breakup process and more accurately estimate fuel atomization in the context of hybrid rocket combustion.
Darsh Nathawani delivered a minisymposium presentation on this research at the 2023 SIAM Conference on Computational Science and Engineering (CSE23), which took place in Amsterdam, the Netherlands, earlier this year. He received funding to attend CSE23 through a SIAM Student Travel Award. To learn more about Student Travel Awards and submit an application, visit the online page.
SIAM Student Travel Awards are made possible in part by the generous support of our community. To make a gift to the Student Travel Fund, visit the SIAM website.
References
[1] Balay, S., Abhyankar, S., Adams, M.F., Benson, S., Brown, J., Brune, P., … Zhang, J. (2021). PETSc/TAO users manual (Technical report ANL-21/39 - Revision 3.16). Lemont, IL: Argonne National Laboratory.
[2] Eggers, J. (1993). Universal pinching of 3d axisymmetric free-surface flow. Phys. Rev. Lett., 71(21), 3458.
[3] Eggers, J., & Dupont, T.F. (1994). Drop formation in a one-dimensional approximation of the Navier–Stokes equation. J. Fluid Mech., 262, 205-221.
[4] Eggers, J., & Villermaux, E. (2008). Physics of liquid jets. Rep. Prog. Phys., 71(3), 036601.
[5] Karabeyoglu, M., & Cantwell, B.J. (2002). Combustion of liquefying hybrid propellants: Part 2, stability of liquid films. J. Propul. Power, 18(3), 621-630.
[6] Nathawani, D.K., & Knepley, M.G. (2022). Droplet formation simulation using mixed finite elements. Phys. Fluids, 34(6), 064105.
[7] Zhang, X., & Basaran, O.A. (1995). An experimental study of dynamics of drop formation. Phys. Fluids, 7(6), 1184-1203.
About the Authors
Darsh Nathawani
Postdoctoral researcher, University at Buffalo
Darsh Nathawani is a postdoctoral researcher in Matthew Knepley’s group at the University at Buffalo. His research involves finite element methods, droplet dynamics, and multiphase flows.

Matthew G. Knepley
Associate professor, University at Buffalo
Matthew G. Knepley is an associate professor in the Department of Computer Science and Engineering at the University at Buffalo. He has been a Portable, Extensible Toolkit for Scientific Computation (PETSc) developer for nearly three decades.

Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



