Elliptical Eyes, Eccentricity, and the Speed of Light

My older son, who enjoyed collecting shiny objects as a boy, kept a glass ball on his windowsill. The ball acted as a lens and burned a quarter-sized dip into the sill. The dip was presumably an approximation of the caustic — the envelope of the family of refracted rays.

This experience prompted the following question: What shape of solid glass would focus the light at a point? I realized that (i) such a shape is an ellipsoid of revolution whose major axis is parallel to the incoming beam; (ii) the eccentricity must equal the speed of light in the glass (taking the speed of light \(c_\textrm{air} =1\)); and (iii) the light will collect at the far focus (see Figure 1).

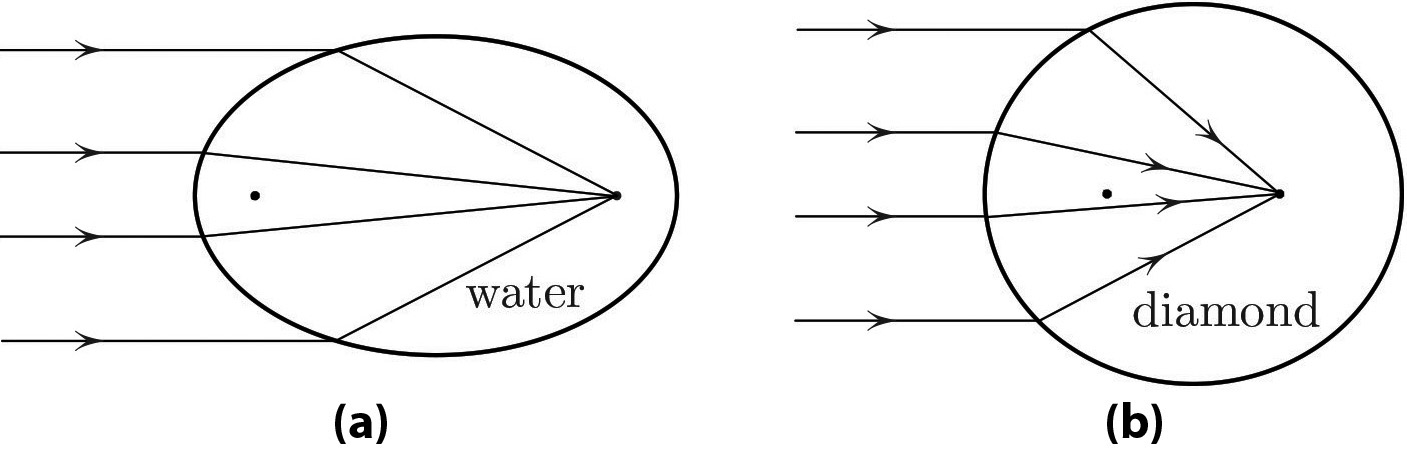
Two interesting limiting cases may deserve a mention: If \(c_\textrm{inside} <<1\), the ellipse is a near-circle and the inside rays are near-radii. If \(c_\textrm{inside} \uparrow 1\), the far focus goes to infinity and the ellipse approaches a parabola. Proof of focusing in Figure 1 is remarkably short. Let \(MN\) in Figure 2 be the ellipse’s directrix, so that \(r=ed\) defines the ellipse with eccentricity \(e\). Differentiation with respect to the arclength parameter of point \(P\) yields

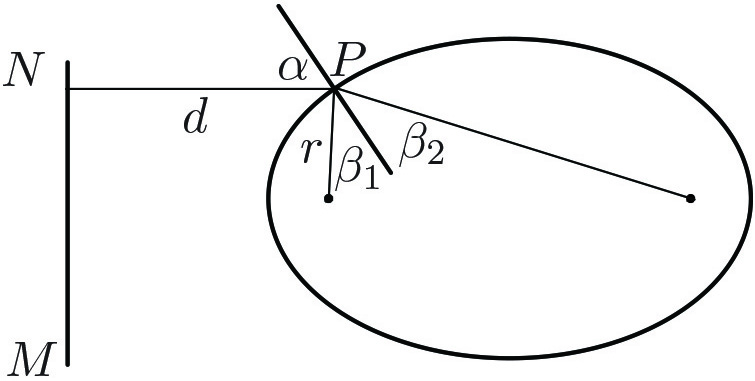
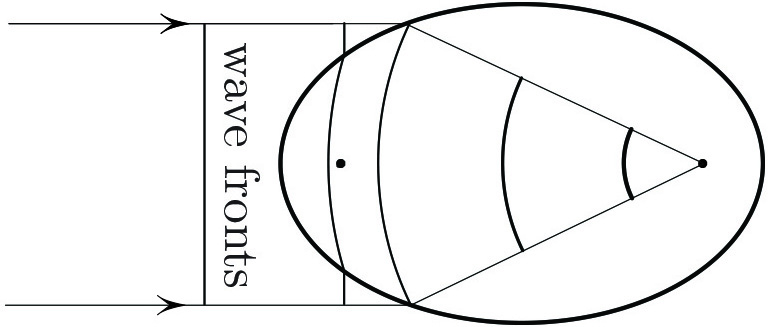
\[\sin \beta_1=e\sin \alpha,\tag1\] since \(r'=\sin \beta_1\) and \(d' = \sin\alpha\), where \(^\prime =d/ds\) and \(s\) is the arclength parameter of \(P\). On the other hand, \(\beta_1=\beta_2\) by the optical property of the ellipse and \((1)\) becomes \[\sin\beta_2=e\sin\alpha.\tag2\] This holds for an ellipse of any eccentricity. But now let us choose \(e=c\), where \(c\) is the speed of light inside the ellipse; \((2)\) then coincides with Snell’s law \[\frac{\sin\beta_2}{c}=\frac{\sin \alpha}{1}, \;\;\;\; 1=c_\textrm{air},\] which proves that the broken line entering the far focus in Figure 2 is indeed a ray’s path. Figure 3 depicts the straight wavefront becoming an arc of a circle upon entering the ellipse.

Interestingly, fluid-filled ellipses act somewhat like parabolic mirrors. Indeed, a point source of light that is placed in a focus of Figure 2 will produce a parallel beam that exits the ellipse. The question as to what happens to the other rays (such as ones that point up from the focus) is left as a puzzle.

This discussion shows that a primitive eye—i.e., one that is filled with an optically homogeneous gel (unlike our eyes, which have lenses inside)—should be elliptical and that the retina should be placed at the far focus.

The figures in this article were provided by the author.