Enhancing Leaf Area Index Simulations With Evidential Deep Learning: A Probabilistic Approach to Uncertainty and Sensitivity

The Community Land Model version 5 (CLM5) [4], a cornerstone of the Community Earth System Model, is a sophisticated tool that simulates terrestrial processes such as carbon cycling, hydrology, and vegetation dynamics [4]. Among its key outputs is the leaf area index (LAI): a dimensionless measure of leaf area per unit ground area that quantifies vegetation canopy coverage. Because LAI governs critical land-atmosphere interactions—including photosynthesis, transpiration, and energy exchange—its accurate simulation is vital for climate modeling, agricultural planning, and ecological forecasting [10]. However, CLM5’s complexity, which stems from its detailed representation of biophysical and biogeochemical processes, introduces significant computational costs and parametric uncertainties for LAI prediction [2].

Here, let us consider LAI as a state variable in a high-dimensional dynamical system. CLM5 integrates differential equations that represent water, energy, and carbon fluxes over a global grid, and LAI emerges as an output that is influenced by dozens of parameters (e.g., photosynthetic rates and nitrogen allocation). The challenge is to efficiently simulate LAI across vast spatiotemporal scales while quantifying the uncertainty that stems from these parameters — tasks that traditional methods struggle to balance with computational feasibility.

Challenges in Emulation

The emulation of CLM5’s LAI outputs poses several mathematical and computational hurdles. First, the model’s high-dimensional parameter space—which spans stomatal conductance, photosynthesis, and hydrology—requires extensive sampling to capture variability, often via perturbed parameter ensembles (PPEs) [11]. For instance, a 500-member PPE may use Latin hypercube sampling to perturb 32 parameters, thereby generating diverse LAI scenarios [6]. However, it is computationally expensive to run CLM5 for each ensemble member over the course of decades, especially at fine resolutions.

Traditional emulators like Gaussian processes (GPs) falter in this context. GPs scale cubically with data size, making them impractical for large PPEs or high-dimensional inputs [5]. They also struggle to preserve LAI’s seasonal periodicity, which is a critical feature for vegetation dynamics. Finally, uncertainty quantification—i.e., distinguishing inherent data noise (aleatoric) from model limitations (epistemic)—remains elusive in standard approaches, thus limiting the utility of GPs for decision-making [3].

Evidential Deep Neural Networks

A deep learning framework called the evidential deep neural network (EDNN) [9] addresses these challenges by emulating CLM5’s LAI with both predictive accuracy and robust uncertainty estimates. Unlike deterministic neural networks that output single-point predictions, EDNNs model the output distribution and leverage the normal-inverse-gamma (NIG) distribution to capture uncertainty [9]. For an input vector \(x_i\) (e.g., perturbed parameters and temporal features), the EDNN predicts four parameters that define the NIG distribution:

• \(\gamma\): Location parameter that approximates the mean \(\mu\)
• \(\nu\): Parameter that controls the variance scale
• \(\alpha\) and \(\beta\): Shape and rate parameters for the inverse gamma component.

We can then model the predicted LAI \(y_i\) as a Gaussian \(N(\mu,\sigma^2)\), where

\[\mu=\gamma,\quad \sigma^2=\frac{\beta}{\nu(\alpha-1)}.\]

Here, \(\sigma^2\) approximates aleatoric uncertainty (i.e., data noise), while epistemic uncertainty (i.e., model uncertainty) scales with \(\frac{\beta}{\alpha-1}\), shrinking as training data increases [9]. The EDNN’s loss function balances fit and uncertainty:

\[L_n(w)=\frac{1}{N}\sum^N_{i=1} L_{NLL,i} (w)+\lambda L_{R,i}(w),\]

where \(L_{NLL,i}\) is the negative log-likelihood of the NIG, \(L_{R,i}\) penalizes overconfidence, and \(\lambda\) is a regularization weight. This formulation is optimized via minibatch stochastic gradient descent; unlike GPs, it enables scalability to large datasets while providing probabilistic outputs in a single forward pass.

EDNN-PPE Temporal Emulation

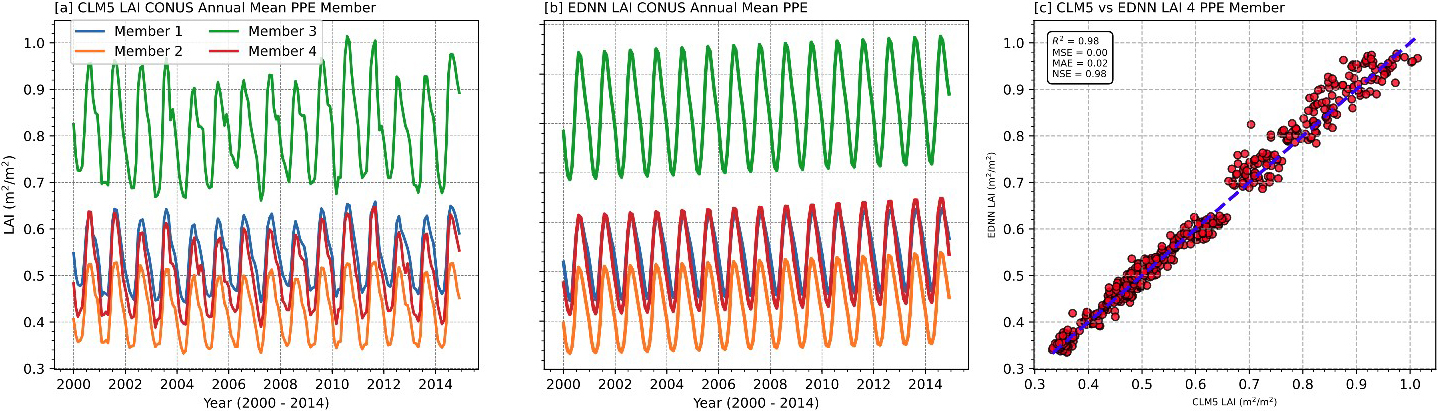
To temporally emulate LAI, the EDNN integrates a 500-member CLM5 PPE that covers 400 global grid cells between the years 1865-2015, with a focus on the contiguous U.S. It cyclically encodes temporal features (months and years), using sine and cosine functions to preserve seasonality; for example, \(\sin(2\pi \cdot \textrm{month}/12)\) ensures continuity between December and January. Doing so expands the input feature set from 32 to 35 parameters, thus enhancing the model’s ability to learn periodic patterns.

The EDNN achieves high accuracy—with \((R^2>0.98)\) for annual mean LAI across ensemble members—and effectively captures seasonal cycles (see Figure 1). However, it struggles with interannual fluctuations, likely due to a lack of climate drivers (e.g., precipitation, temperature, and evapotranspiration) in the training data for the EDNN model. This shortcoming highlights the tradeoff between computational efficiency and full process representation.

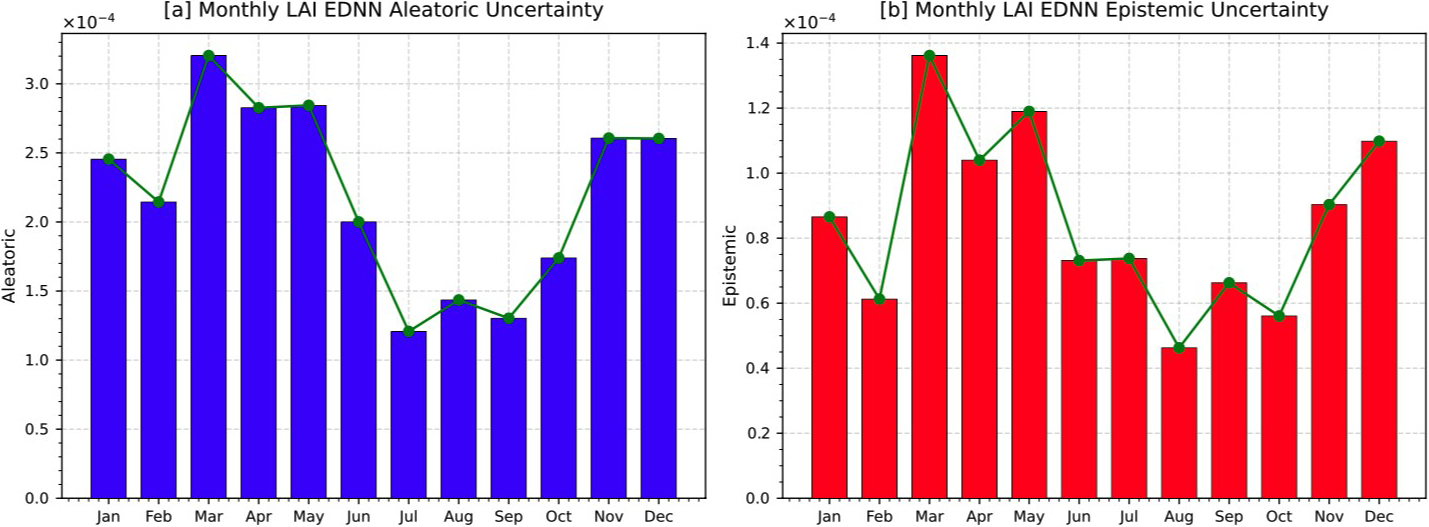
Monthly Aleatoric and Epistemic Uncertainty

The EDNN’s uncertainty decomposition reveals distinct monthly patterns in LAI reliability (see Figure 2). Aleatoric uncertainty, which reflects biophysical noise, peaks in late winter to early spring (e.g., February-March)—driven by snow cover and phenological transitions—then dips in late summer as vegetation stabilizes. Epistemic uncertainty, which is tied to model or data limitations, rises in spring (e.g., May) during rapid canopy growth before falling in autumn and winter.

Mathematically, the law of total variance decomposes total uncertainty as

\[\textrm{Total Variance}=E[\sigma^2]+\textrm{Var}[\mu],\]

where \(E[\sigma^2]\) is aleatoric and \(\textrm{Var}[\mu]\) is epistemic (computed from NIG parameters). This differentiation guides model refinement, as high epistemic uncertainty in spring suggests data gaps or parameterization issues.

Parameter Sensitivity Analysis

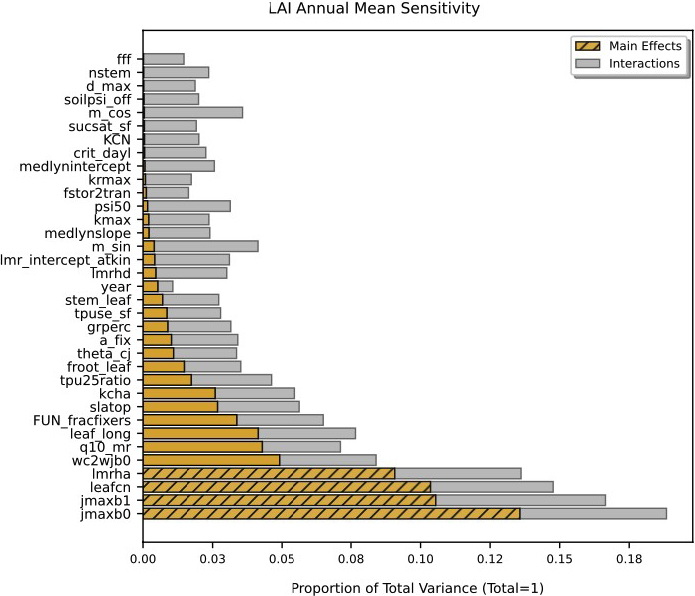
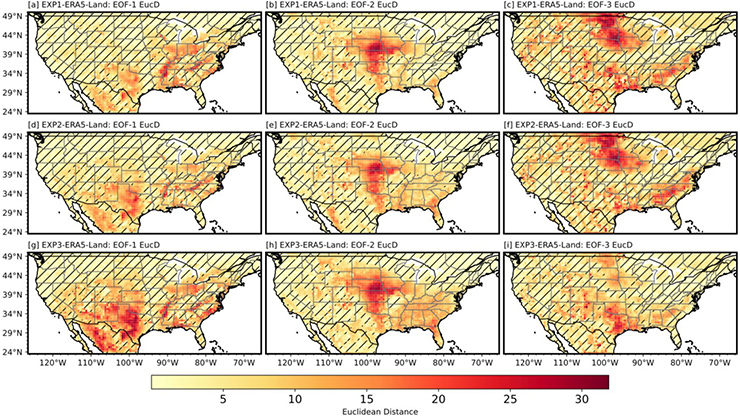
The Fourier amplitude sensitivity test (FAST) [8] identifies key parameters that drive LAI variability, using the EDNN as a surrogate to reduce computational cost. FAST decomposes LAI variance into main effects (direct parameter contributions) and interactions:

\[\textrm{Total Variance}=\sum_i V_i + \sum_{i<j} V_{ij}+ \cdots.\]

Here, \(V_i\) is the variance from parameter \(i\) and the higher-order terms capture interactions. Figure 3 displays annual parameter sensitivities. Photosynthetic parameters (jmaxb0 and jmaxb1) dominate throughout the year; jmaxb0 explains roughly 13 percent of variance, which reflects the role of nitrogen allocation in electron transport. Leaf carbon-to-nitrogen ratio (leafcn) gains influence in the autumn and winter, while interactions amplify in transitional seasons — an indication of complex dependencies.

Practical Implications

The EDNN framework offers a scalable, uncertainty-aware alternative to full CLM5 runs, reducing simulation time from weeks to hours while retaining accuracy. Its successful identification of sensitive parameters (e.g., jmaxb0 and leafcn in Figure 3) prioritizes field data collection and calibration efforts to enhance model realism [7]. This work exemplifies deep learning’s utility to tackle high-dimensional, nonlinear problems in Earth sciences by connecting process-based modeling with data-driven insights. Future research could integrate observational LAI data (e.g., remote sensing) into a Bayesian framework, leveraging EDNN’s uncertainty estimates to further refine predictions [1].

Acknowledgments: The author conducted this work in collaboration with Alejandro Flores and Irene Cionni of Boise State University, Linnia Hawkins of Columbia University, and Charlie Becker and Katherine Dagon of the U.S. National Science Foundation’s (NSF) National Center for Atmospheric Research. The team gratefully acknowledges support from the NSF and other institutions that facilitated this research.

References
[1] Asch, M., Bocquet, M., & Nodet, M. (2016). Data assimilation: Methods, algorithms, and applications. Philadelphia, PA: Society for Industrial and Applied Mathematics.
[2] Fisher, R.A., & Koven, C.D. (2020). Perspectives on the future of land surface models and the challenges of representing complex terrestrial systems. J. Adv. Model. Earth Syst., 12(4), e2018MS001453.
[3] Hawkins, E., & Sutton, R. (2009). The potential to narrow uncertainty in regional climate predictions. Bull. Amer. Meteor. Soc., 90(8), 1095-1107.
[4] Lawrence, D.M., Fisher, R.A., Koven, C.D., Oleson, K.W., Swenson, S.C., Bonan, G., ... Zeng, X. (2019). The Community Land Model version 5: Description of new features, benchmarking, and impact of forcing uncertainty. J. Adv. Model. Earth Syst., 11(12), 4245-4287.
[5] Liu, X., & Guillas, S. (2017). Dimension reduction for Gaussian process emulation: An application to the influence of bathymetry on tsunami heights. SIAM/ASA J. Uncertain. Quantif., 5(1), 787-812.
[6] McKay, M.D., Beckman, R.J., & Conover, W.J. (1979). A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics, 21(2), 239-245.
[7] Ricciuto, D., Sargsyan, K., & Thornton, P. (2018). The impact of parametric uncertainties on biogeochemistry in the E3SM land model. J. Adv. Model. Earth Syst., 10(2), 297-319.
[8] Saltelli, A., Ratto, M., Andres, T., Campolongo, F., Cariboni, J., Gatelli, D., ... Tarantola, S. (2008). Global sensitivity analysis: The primer. Chichester, England: John Wiley & Sons.
[9] Schreck, J.S., Gagne II, D.J., Becker, C., Chapman, W.E., Elmore, K., Fan, D., ... Wirz, C. (2024). Evidential deep learning: Enhancing predictive uncertainty estimation for Earth system science applications. Artif. Intell. Earth Syst., 3(4), 230093.
[10] Sellers, P.J., Dickinson, R.E., Randall, D.A., Betts, A.K., Hall, F.G., Berry, J.A., ... Henderson-Sellers, A. (1997). Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science, 275(5299), 502-509.
[11] Stainforth, D.A., Aina, T., Christensen, C., Collins, M., Faull, N., Frame, D.J., ... Allen, M.R. (2005). Uncertainty in predictions of the climate response to rising levels of greenhouse gases. Nature, 433(7024), 403-406.