Evaporation and the Coffee Ring Effect for Noncircular Droplets

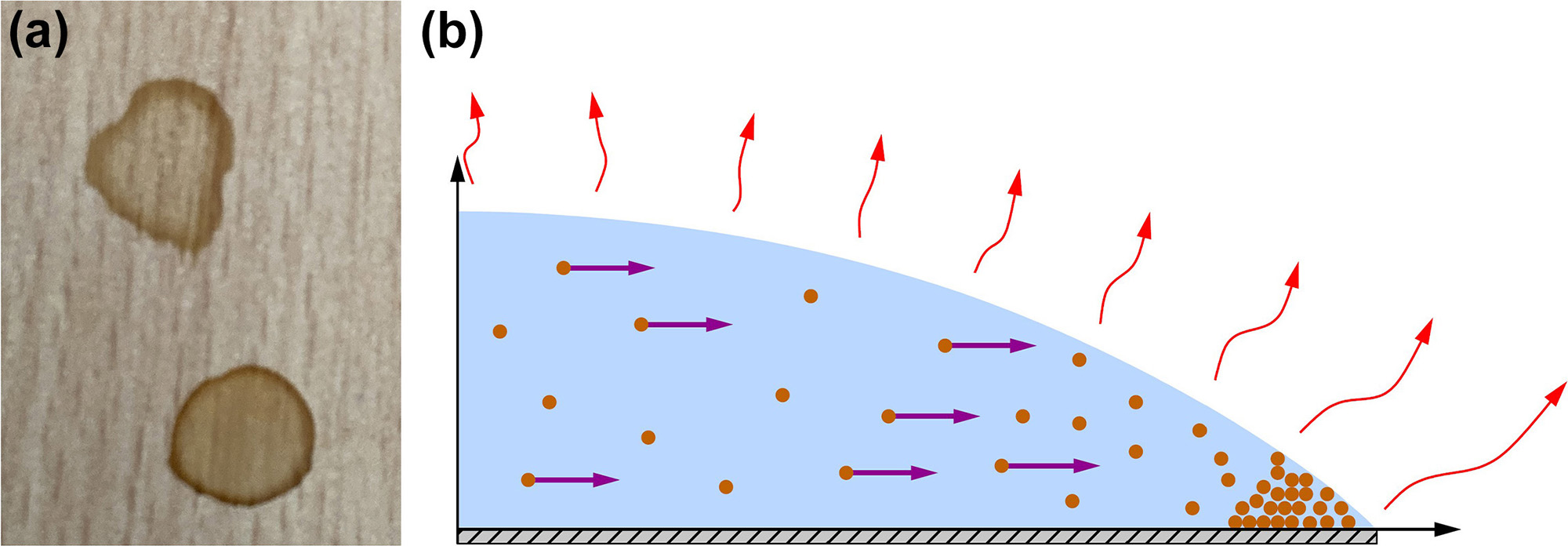
Have you ever wondered why a spilled drop of coffee leaves a stain on the table that is darker towards the edge than in the center? The eponymous “coffee ring” effect occurs almost universally when particle-laden droplets evaporate into the surrounding atmosphere [1]. In short, the edge of the droplet—i.e., its contact line—becomes pinned to the surface upon which it sits. To conserve mass and replace the fluid that is lost as the droplet dries, a flow is driven from the center of the droplet towards its contact line. This flow carries particles outwards, increasing the concentration at the edges (see Figure 1).

Despite its seemingly innocuous nature, the coffee ring effect is important to many industrial processes. It finds applications in colloidal patterning, microscale printing, and DNA analysis but may be undesirable in inkjet printing or the production of organic light-emitting diode (OLED) screens, whereby millions of small nanodroplets are printed in arrays that become the pixels on smartphone screens. Understanding the dynamics of coffee ring formation is therefore a critical engineering challenge, particularly in the context of control problems [3]. However, the number of interacting parts complicates the associated mathematics.

One key component involves determining the rate at which fluid evaporates. Because evaporation is a slow process for the small droplets that are involved in microscale and nanoscale fabrication, the relevant calculation for the vapor concentration \(c(r, \theta, z)\) is a classical diffusion problem. Here, we use a cylindrical polar coordinate system whose origin is within the droplet footprint \(\Omega\); the solid surface is hence given by \(z=0\) and the droplet surface is given by \(z=h(r,\theta)\) for \((r,\theta)\in\Omega\). Thus, \(c\) satisfies

\[\nabla^2c=0 \; \textrm {in the air}, \quad c=1 \; \textrm{on} \; z=h(r, \theta)\in\Omega, \quad \frac{\partial c}{\partial z}=0 \; \textrm{on} \; z=0,(r,\theta) \notin \Omega, \quad c\rightarrow 0 \; \textrm{as} \; |(r,\theta,z)|\rightarrow \infty. \tag1\]

In this mixed boundary value problem, the boundary condition changes type from Dirichlet on the droplet surface to Neumann on the solid surface. Mathematically identical problems arise across a variety of physical systems, including electrostatics (where \(c(r,\theta,z)\) plays the role of the electrostatic potential) and heat transfer (where \(c(r,\theta,z)\) is the temperature).

From a mathematical standpoint, mixed boundary value problems are notoriously challenging. The change in boundary conditions leads to singular behavior at the edge of the droplet \(\partial\Omega\), which complicates direct computations — particularly in the context of multiple droplets. As such, there are very few analytical solutions to \((1)\), and those that do exist are typically restricted to simple geometries like circular or elliptical droplets or spherical or ellipsoidal caps. The geometry is often more complicated in practical contexts, such as the use of square or hexagonal droplets to print OLED pixels. We aim to tackle this thorny issue by developing an asymptotic solution for arbitrary geometries.

Evaporation Model

Our mathematical model focuses on two approximations. First, we assume that the droplets are thin — i.e., for a droplet with a typical contact radius \(R\) and initial maximum height \(H\), we assume that \(H/R \ll 1\). Such an approximation is reasonable in real-world scenarios; for example, \(H/R \approx 0.08\) for the printed pixels in a 2021 study [2]. This assumption allows us to linearize the boundary condition on the droplet-free surface in \((1)\) onto \(z=0\). We can then use a Green’s function to turn the mixed boundary value problem into an equivalent integral equation

\[1=\frac{1}{2\pi}\int\int_{(r,\theta)\in\Omega} \frac{r'J(r',\theta')}{\sqrt{r^2+r'^2-2rr'\cos(\theta-\theta'})}\textrm{d}r'\,\textrm{d}\theta' \quad \textrm{for} \quad (r,\theta)\in\Omega. \tag2\]

Here, the goal is to determine the evaporative flux \(J(r,\theta)=-(\partial c/\partial z)(r, \theta, 0)\), which is the required piece of information for the analysis of flow and particle transport within the droplet.

This integral equation is not explicitly solvable for a general contact line; the difficulty arises in the integral limits due to the general nature of \(\Omega\). Indeed, we can explicitly solve the integral when \(\Omega\) is simply a circle, which has been known since 1873 [7]. This knowledge inspires our second approximation, wherein we first consider a droplet whose contact line is nearly circular, with dimensionless monochromatic form

\[r=1+\varepsilon \cos n\theta, \quad \textrm{where} \quad 0<\varepsilon \ll 1 \tag3\]

and \(n \in \mathbb{N}_{\ge 2}\). The small parameter \(\varepsilon\) enables the use of asymptotic analysis to break the integral equation into a series of solvable problems. We write the evaporative flux \(J\) in terms of a series of powers of \(\varepsilon\)—i.e., \(J=J_0(r,\theta)+\varepsilon J_1(r, \theta)+\varepsilon^2 J_2 (r,\theta)+O(\varepsilon^3)\)—and similarly expand the integral limits in powers of \(\varepsilon\). By comparing powers of \(\varepsilon\), we may then successively find each \(J_i\) by inverting the integral, since the expansion of the limit means that the inversion’s domain is just a circle to the respective order.

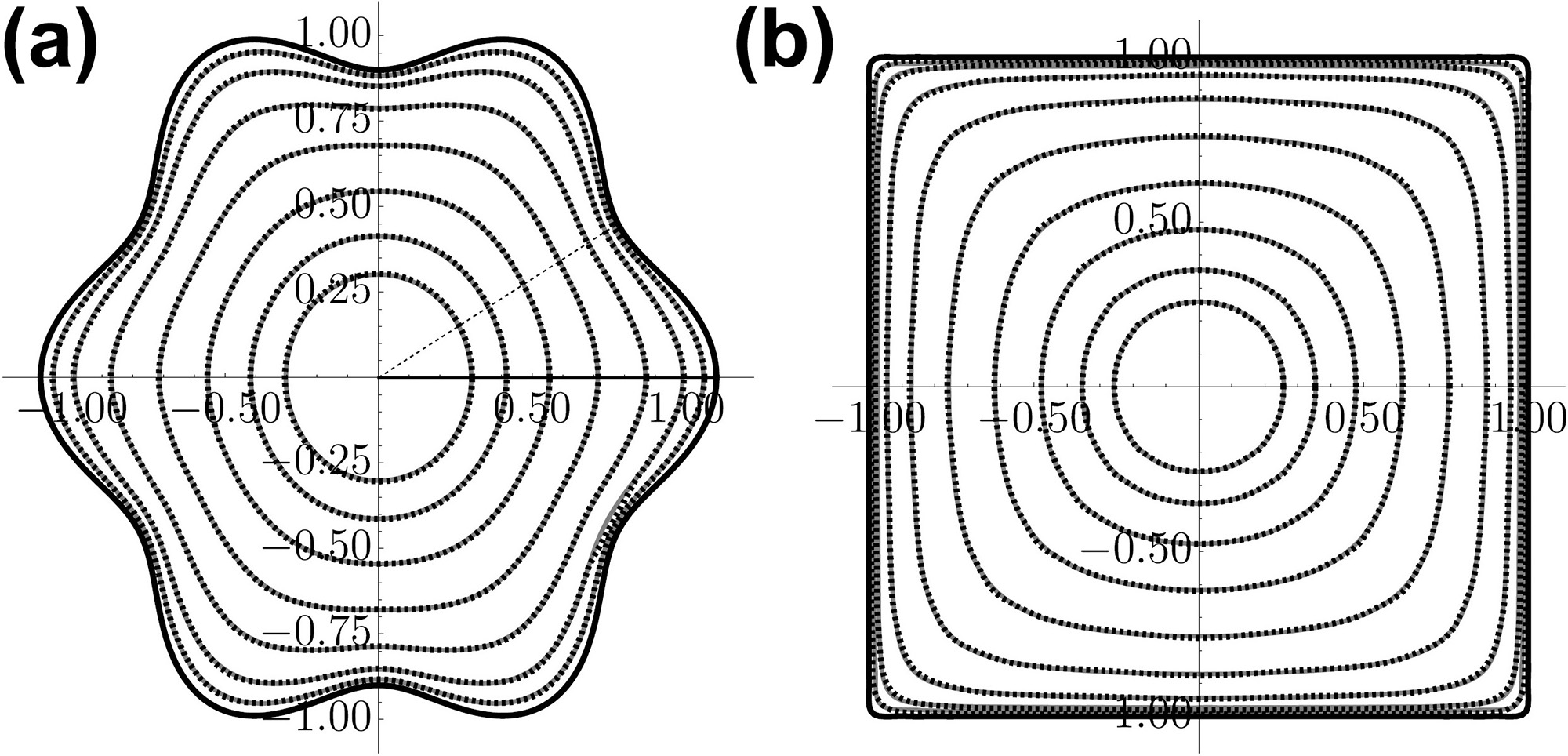
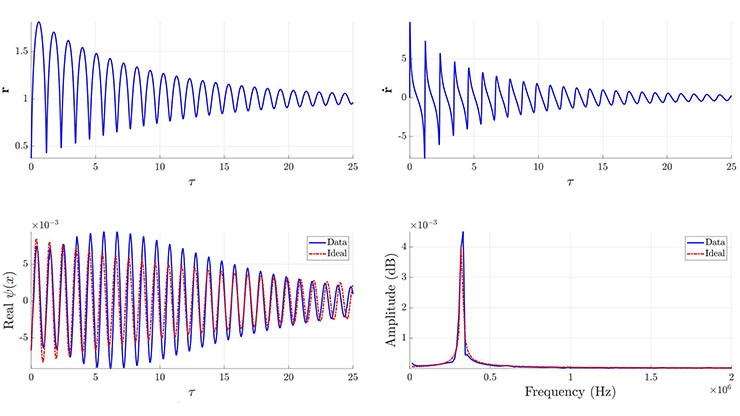
Although the resulting functions are complicated, we can write them explicitly as functions of \((r,\theta)\); doing so makes them significantly faster to compute than direct numerical simulations that use techniques such as finite element methods. Figure 2a depicts an example contour of constant \(J\) from our asymptotic solution for \(n=6\), \(\varepsilon=0.1\), as compared to the results of a typical finite element solver called COMSOL. The method of approximation obtains the evaporative flux remarkably well; in fact, the integral of the absolute relative error along a radial ray is below 0.5 percent. This is certainly an acceptable outcome, especially when we consider that \(\varepsilon=0.1\) is not particularly small.

The success of this approach means that we can handle more complicated geometries that are far from circular. For a given contact line \(r=f(\theta)\), we find the Fourier series of \(f(\theta)\), say

\[f(\theta)=1+\sum^n_{i=2}(c_i\cos i\theta+d_i\sin i\theta). \tag4\]

After suitable truncation, we can then use the individual fluxes that we calculated for each term of the series to define the evaporative flux. This procedure is extremely robust due in part to the geometry, as the coefficients of the series are such that \(|c_i|,|d_i|<1\) for all \(i\); and for smooth droplets, the coefficients decay rapidly as \(i\) increases.

Figure 2b displays results for a sample square droplet. Comparisons between the asymptotic solution and full simulations are once again excellent, with a similar measure of absolute relative error at \(\lesssim\) 2 percent.

Application to Coffee Rings

Now that we’ve validated our asymptotic solution for the evaporative flux, we can simply incorporate it within a model of the liquid flow and particle transport in a droplet. Under the thin assumption, we presume that the velocity \(\mathbf{u}\) and particle distribution \(\phi\) in the droplet are independent of \(z\) and satisfy

\[\begin{eqnarray}\nabla \cdot (h\mathbf{u})&=&-\frac{\partial h}{\partial t}-J, \tag 5 \\ \mathbf{u}&=&\frac{h^2}{3\textrm{Ca}}\nabla(\nabla^2h), \tag 6 \\ \frac{\partial}{\partial t}(h\phi)+\nabla \cdot \bigg(h\phi\mathbf{u}-\frac{h}{\textrm{Pe}}\nabla\phi\bigg)&=&0. \tag7 \end{eqnarray}\]

Here, \((5)\) and \((6)\) are the lubrication equations for viscous thin films, and \((7)\) is an advection-diffusion equation for particle transport inside the droplet. The dimensionless capillary number \(\textrm{Ca}\) measures the relative importance of surface tension and viscosity in the droplet, and the Péclet number \(\textrm{Pe}\) measures the relative importance of diffusion and advection of the particles.

For real-world applications like OLED screen printing, \(\textrm{Ca}\) tends to be small because surface tension is the dominant effect in the droplet shape. \(\textrm{Pe}\), however, is generally large because advection dominates in the majority of the droplet, though particle diffusion plays a key role near the contact line in determining the early shape of the coffee ring [4].

With \(J\), in hand, we can solve \((5)\)-\((7)\) (subject to suitable initial and boundary conditions) to find the final distribution in the droplet. In Figure 3, we perform this analysis for the triangular droplets from a previous study [5]. Figure 3a depicts the final deposit of an evaporating coffee droplet from this experiment, while Figure 3b illustrates the extracted distribution of particle mass as compared to our model’s predictions — as we can see, the agreement is excellent! Further details are available in [8].

Future Directions

We have developed an accurate and flexible asymptotic method to determine the rate at which arbitrarily shaped droplets evaporate. The next step is to expand this solution into a usable model for practical industrial applications. Doing so will require the consideration of large arrays of multiple square droplets, as OLED screens can contain on the order of hundreds of millions of pixels [6]; calculations for such large arrays are understandably quite challenging. Nevertheless, our analytical solution for evaporative flux is the first step towards practically analyzing and ultimately controlling the coffee ring effect in such settings.

Madeleine Moore delivered a minisymposium presentation about this research at the 10th International Congress on Industrial and Applied Mathematics, which took place in Tokyo, Japan, last year.

References
[1] Deegan, R.D., Bakajin, O., Dupont, T.F., Huber, G., Nagel, S.R., & Witten, T.A. (1997). Capillary flow as the cause of ring stains from dried liquid drops. Nature, 389(6653), 827-829.
[2] Jin, Y., Chen, J., Yin, Z., Li, Y., & Huang, M. (2021). Positioning error limit for the last droplet deposition into a microcavity in the manufacture of printed OLEDs. Langmuir, 37(31), 9396-9404.
[3] Mampallil, D., & Eral, H.B. (2018). A review on suppression and utilization of the coffee-ring effect. Adv. Colloid Interface Sci., 252, 38-54.
[4] Moore, M.R., Vella, D., & Oliver, J.M. (2021). The nascent coffee ring: How solute diffusion counters advection. J. Fluid Mech., 920, A54.
[5] Sáenz, P.J., Wray, A.W., Che, Z., Matar, O.K., Valluri, P., Kim, J., & Sefiane, K. (2017). Dynamics and universal scaling law in geometrically-controlled sessile drop evaporation. Nat. Commun., 8(1), 14783.
[6] Virey, E.H., Baron, N., & Bouhamri, Z. (2020). 30-4: MicroLED display technology trends and intellectual property landscape. SID Symp. Dig. Tech. Pap., 51(1), 436-439.
[7] Weber, H. (1873). Über die Besselschen functionen und ihre anwendung auf die theorie der elektrischen ströme. J. Reine Angew. Math., 75, 75-105.
[8] Wray, A.W., & Moore, M.R. (2024) High-order asymptotic methods provide accurate, analytic solutions to intractable potential problems. Sci. Rep., 14(1), 4225.