Exploring the Dynamics of Viral Spread: Insights From DS25
The 2025 SIAM Conference on Applications of Dynamical Systems (DS25), which took place in Denver, Colo., last month, brought together a global community of researchers to explore the role of mathematics in various real-world phenomena. Among the many engaging events was a three-part series of minisymposium sessions titled “Dynamical Systems in Mathematical Biology: Disease Modeling and Biological Processes,” which offered an interdisciplinary perspective on dynamical systems in mathematical biology. The series showcased recent advancements in mathematical models of biological systems, including disease dynamics.
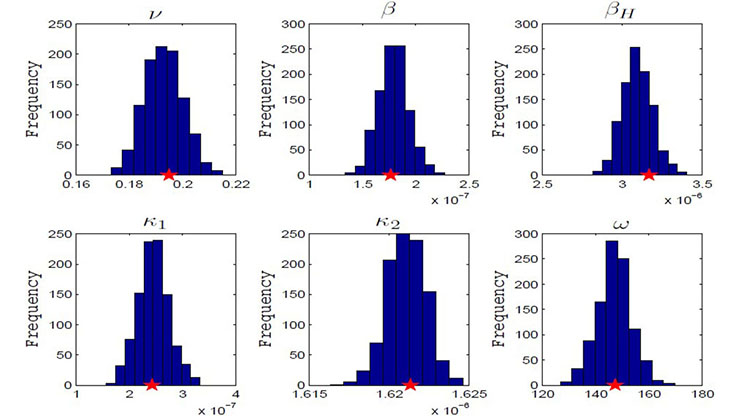
![<strong>Figure 1.</strong> Backward bifurcation diagram for the fixed parametric values with \(n=2\). The blue and red lines respectively denote stable and unstable equilibrium points. Figure courtesy of [2].](/media/eezpdfmw/figure1.jpg)
During the minisymposium, I presented a talk about the dynamics of virus spread. My group’s work provides a rigorous, biologically motivated analysis of infectious disease dynamics in environments where viral particles persist outside of the human host, such as on surfaces, in aerosols, or in contaminated water [2].
Classical compartmental epidemic models—like the susceptible-infected-recovered framework—generally assume that disease transmission only occurs through direct contact between individuals. Our model departs significantly from this assumption by incorporating indirect transmission via an environmental viral reservoir; this addition reflects real-world conditions for diseases such as cholera, norovirus, and respiratory viruses like SARS-CoV-2, where environmental persistence contributes to continued transmission. The model considers a system of six differential equations that describe the flow between five compartments: susceptible (S), exposed (E), infected (I), vaccinated (V), and recovered (R) individuals. It also accounts for the concentration of virus in the environment (C) through a response function \(g(C,\kappa)\), which describes the concentration’s effect on the rate of infection via the environmental route [1, 3]. This function depends on an integer \(n \geq 1\).
A key finding from our study is the occurrence of backward bifurcations for certain parameter values, particularly when \(n=2\) (see Figure 1). Here, an endemic steady state can exist even though the basic reproduction number \((R_0)\) is less than \(1\). This possibility indicates that reducing \(R_0\) to less than \(1\) may not sufficiently eradicate the disease in question, thus highlighting the importance of environmental transmission and vaccination efficacy in disease control strategies.
We also investigated the stability of the disease-free equilibrium (DFE) and endemic equilibria. Using the Routh-Hurwitz criterion as well as more restrictive conditions, we proved the local stability of the DFE for \(R_0\), then utilized the method of Pauline van den Driessche and James Watmough [5] to analyze the existence of backward bifurcations. Additionally, our study examined the number of positive steady states and their stability for arbitrary values of \(n\) [4].
![<strong>Figure 2.</strong> Vaccination component of the model with \(n=2\), compared with real data from the period between June 10, 2021, and August 8, 2021. For the fixed parameters and initial conditions, we choose \(S_0 = 61{,}098{,}000\), \(V_0 = 18{,}500{,}000\), \(E_0 = 2{,}200{,}000\), \(R_0 = 2{,}000\), and \(C_0 = 20{,}000\). The black line denotes the model result and the red stars represent daily vaccinated cases. Figure courtesy of [2].](/media/z03bynrk/figure2.jpg)
We conducted numerical simulations to compare the model's predictions with COVID-19 data from Türkiye and demonstrate its applicability to real-world scenarios (see Figure 2). Sensitivity analysis identified the most influential parameters that affect \(R_0\) and the dynamics of disease spread. Our study concluded that the occurrence of backward bifurcations, which can be important for disease control strategies, is dependent on the details of the function that describes the force of infection — a result that underscores the need for careful attention to environmental transmission pathways and vaccination effects in epidemiological models. The research also points toward future extensions with climate-driven effects; since environmental factors like temperature and humidity influence virus survival, the integration of these variables into transmission models could help predict shifting disease dynamics amid a changing climate.
Other talks in the three-part session explored a variety of biological and medical applications, including bifurcation in cancer progression, oscillatory immune responses, and reaction-diffusion models for spatial spread. For these and other topics, the use of dynamical systems provided a rigorous mathematical lens to understand complex feedback mechanisms in biology and medicine. The minisymposium facilitated lively discussions and new connections across disciplines, highlighting the increasingly significant role of applied mathematics in biological challenges. Overall, DS25 was a rewarding experience for attendees, with broad participation from researchers at a wide range of career stages and institutions.
Burcu Gürbüz delivered a minisymposium presentation on this research at the 2025 SIAM Conference on Applications of Dynamical Systems, which took place in Denver, Colo., this May.
Acknowledgments: I would like to thank the speakers in our DS25 minisymposium; Johannes Gutenberg University Mainz; and the grantors who supported the associated research projects, visits, and session organization, including the Johanna Quandt Young Academy, Dres. Goebel Klima-Stiftung, and European Mathematical Society. I am also grateful to SIAM for supporting and hosting DS25 and other conferences, which continue to advance the global applied mathematics community.
References
[1] Bulut, H., Gölgeli, M., & Atay, F.M. (2021). Modelling personal cautiousness during the COVID-19 pandemic: A case study for Turkey and Italy. Nonlinear Dyn., 105(1), 957-969.
[2] Gökçe, A., Gürbüz, B., & Rendall, A.D. (2024). Dynamics of a mathematical model of virus spreading incorporating the effect of a vaccine. Nonlinear Anal. Real World Appl., 78(1-2), 104097.
[3] Gumel, A.B., McCluskey, C.C., & Watmough, J. (2006). An SVEIR model for assessing potential impact of an imperfect anti-SARS vaccine. Math. Biosci. Eng., 3(3), 485-512.
[4] Martcheva, M. (2019). Methods for deriving necessary and sufficient conditions for backward bifurcation. J. Biol. Dyn., 13(1), 538-566.
[5] Van den Driessche, P., & Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci., 180(1-2), 29-48.
About the Author
Burcu Gürbüz
Postdoctoral researcher, Johannes Gutenberg University Mainz
Burcu Gürbüz is a postdoctoral researcher in the Institute of Mathematics at Johannes Gutenberg University Mainz in Germany. Her main research interests include dynamical systems, differential equations, qualitative analysis, mathematical biology, numerical methods, and programming. Among other works, Gürbüz uses mathematical methods to construct and analyze models that improve our understanding of the climate system.

Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.