Flight at Low Reynolds Numbers: The Aerodynamics of Tiny Insects
Despite their minuscule size (with body lengths under two millimeters), the smallest flying insects are of considerable agricultural and ecological importance. For example, parasitoid wasps serve as biocontrol agents in agricultural and forest ecosystems, while thrips are infamous for damaging crops and ornamental plants. Detailed insight into the flight mechanisms of these miniature organisms may lead to improved biocontrol strategies and novel techniques that minimize agricultural losses [3]. On the more technical side, such insights can also aid in the design and development of micro aerial vehicles or miniature drones for environmental monitoring, surveillance, examination of cramped spaces, and so forth.
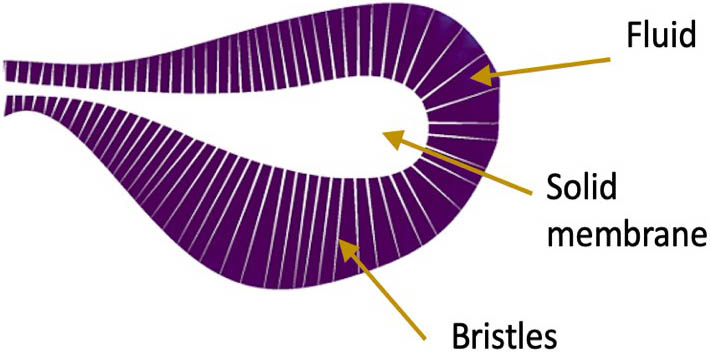
We focus on two aspects of small insect flight: the presence of wing bristles and wing flexibility. The wing surfaces of most tiny insects are covered in long, hair-like bristles that attach to the relatively narrow, membranous section of the wing in an arrangement that looks somewhat like a comb (see Figure 1). Why do the wings have this structure, rather than the membranous wings that are characteristic of larger insects? Revealing the aerodynamic benefits of bristled wings was our first goal.

The second part of our study focused on wing flexibility. Recordings of tiny insects in flight suggest that their wings are relatively rigid or exhibit a low level of flexibility. Would greater flexibility in their wings augment their natural flight performance? Based on these questions, our study focused on the effects of bristles and wing flexibility on the hovering flight performance of tiny insects.
Methodology
Given the significance of both viscosity and inertia in the airflows that surround tiny insects, we considered the full Navier-Stokes equations. The problem is inherently three-dimensional (3D) with moving boundaries, so we conducted our investigations via computational fluid dynamics. We employed the immersed boundary (IB) method to solve the fully coupled fluid-structure interaction problem for a pair of flexible, flapping wings in a viscous fluid (e.g., air). The IB method—which was originally developed by Charles Peskin [7]—uses a Lagrangian description for a structure that is immersed in a fluid and a Eulerian description for the governing equations of fluid motion: the Navier-Stokes equations. Researchers have utilized this popular method for the simulation of fluid-structure interactions to study topics including blood flow in the heart, jellyfish hydrodynamics, and the fluid dynamics of pulsing corals and nematocyst firing. We implemented a hybrid finite difference/finite element version of the IB method [2] that relied on the IBAMR (Immersed Boundary Method Adaptive Mesh Refinement Software Infrastructure) software library, which is a distributed-memory parallel implementation of the IB method. More details about IB in general are available in literature [5-7].
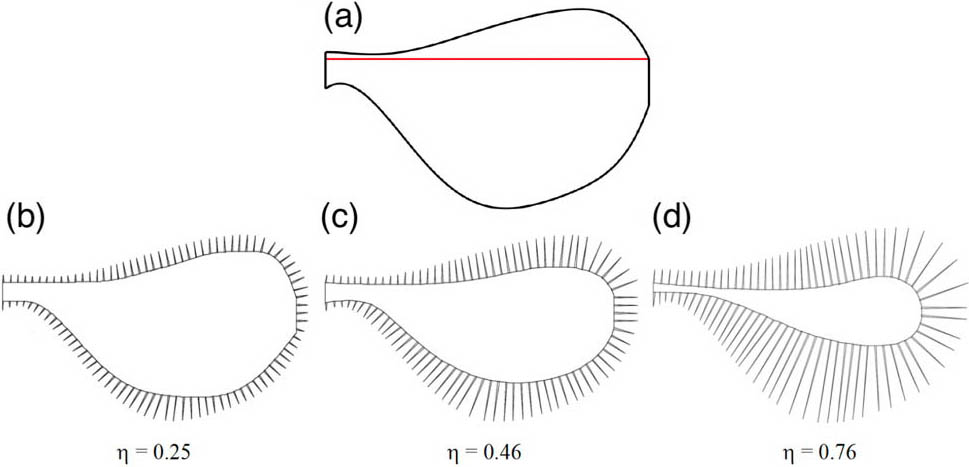
We centered our study around the hovering kinematics that are employed by the tiny parasitoid wasp Encarsia formosa (see Animation 1), and our base/reference wing was a membranous approximation of Encarsia formosa’s wing (see Figure 2) [1]. To understand the role of bristles, we generated three different bristled wings by adding bristles to our reference wing while conserving the wing’s effective area. These wings ranged from least to most bristled, which is analogous to real-life tiny insects.
Our study mainly focused on spanwise flexibility, wherein a part of the wing near the base is rigid while the remainder deforms in response to forces from the surrounding air. Starting from the base case, we generated five flexible wings that ranged from least to most flexible (see Figure 3). The normalized Young’s moduli of these wings are as follows: \(7.4 \times 10^7\) (least flexible), \(4.94 \times 10^7\), \(3.02 \times 10^7\), \(1.10 \times 10^7\), and \(4.00 \times 10^6\) (most flexible). The first three wings were moderately flexible and the remaining two were highly flexible in the spanwise direction.

Finally, we introduce the Reynolds number (\(Re\)) and aerodynamic performance parameters of interest. \(Re\) is a dimensionless number that measures the ratio of inertial to viscous forces in fluid flows and is given by \(\rho\textrm{LU}/\mu\). Here, \(\rho\) is the fluid density, \(\mu\) is the dynamic viscosity of the fluid, \(\textrm{U}\) is the wingtip velocity, and \(\textrm{L}\) is the wing’s chord length. The range of relevant \(Re\) for tiny insect flight is \(4\) to \(60\), so we selected the following \(Re\) for this study: \(4\), \(8\), \(16\), \(32\), and \(64\). We also quantified wing performance with vertical and horizontal force. Vertical force is the component of the net fluid force on a wing that acts parallel to the direction of gravity, while horizontal force is the component that acts perpendicular to gravity. Since our study concerns the hovering maneuver, our focus will primarily remain on the vertical force.
Results and Discussion
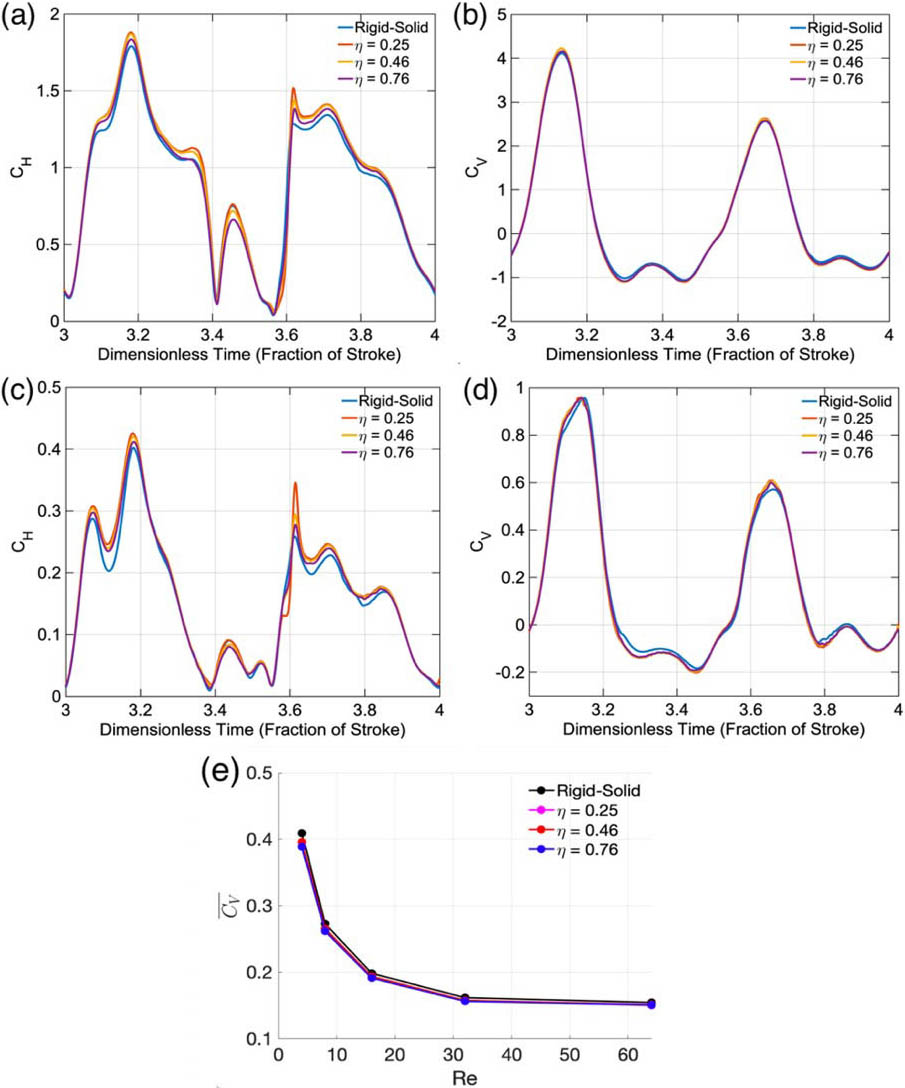
We performed IB simulations for the membranous, bristled, and flexible wings at \(Re\) values ranging from \(4\) to \(64\). The bristled wings exhibited excellent agreement with the membranous wings in terms of the force coefficients \((\textrm{C}_\textrm{V}\) and \(\textrm{C}_\textrm{H})\) over the entire \(Re\) range. For example, Figure 4 shows \(\textrm{C}_\textrm{V}\) and \(\textrm{C}_\textrm{H}\) as functions of dimensionless time for the membranous and bristled wings at \(Re=4\) and \(Re=64\). Since the instantaneous vertical force was nearly identical for the membranous and bristled wings, their time-averaged vertical force coefficients exhibited good agreement.
To explain the good agreement between the bristled and membranous wings, we examined the distribution of the fluid velocity’s normal component (relative to the wing) in the gaps between the bristles of the bristled wings (see Figure 5). It is evident that this component was negligible throughout the entire stroke. Therefore, it may be appropriate to say that the fluid in the bristle gaps remains nearly static relative to the wing during the hovering of tiny insects — in other words, the fluid “sticks” to the wing. As a result, the bristled wings are essentially transformed into membranous wings that simply have a different configuration consisting of fluid, bristles, and a solid membrane (see Figure 6). This outcome explains the force equivalence between the bristled and membranous wings.
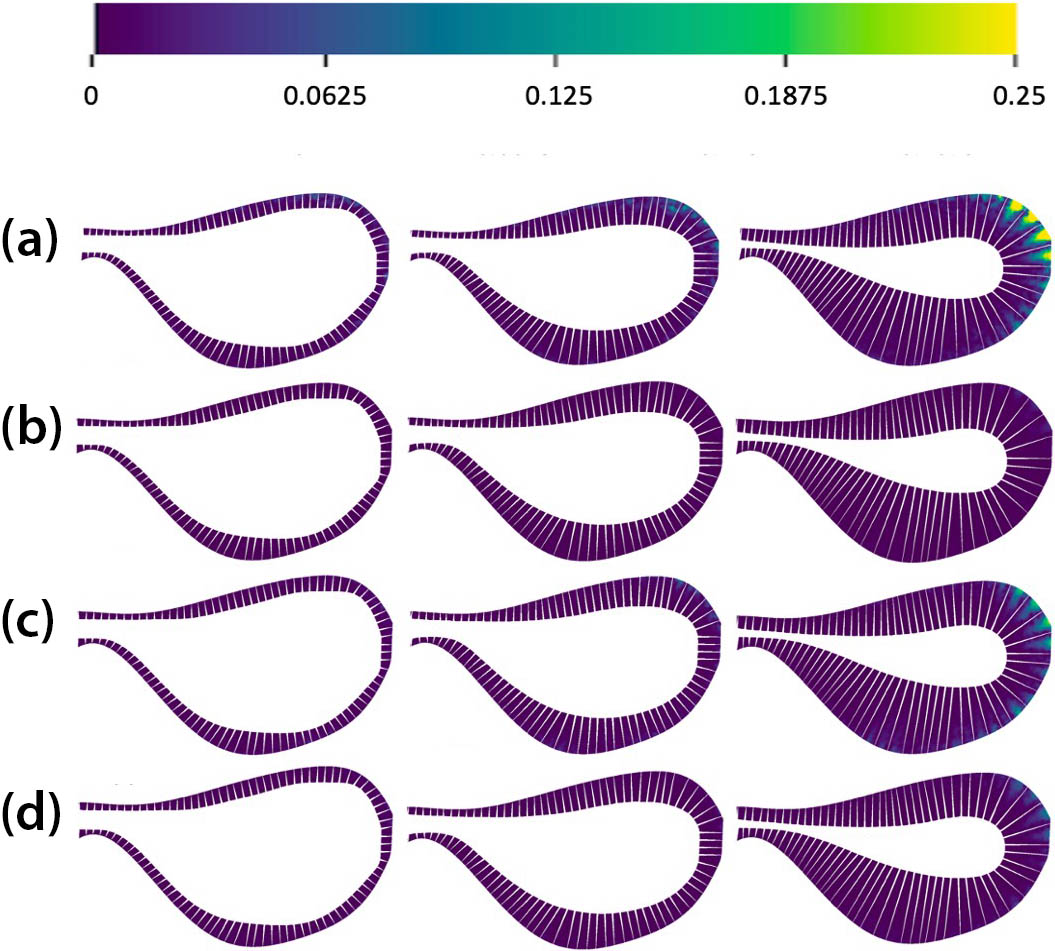
These results suggest that for hovering in tiny insect flight, bristled wings generate nearly as much average vertical force as membranous wings. The lower mass of bristled wings means that they require much less energy to flap than membranous wings. Therefore, bristled wings possess a higher hovering energy efficiency than membranous wings.
We next move to our results for flexible wings. Figure 7 illustrates the instantaneous and time-averaged vertical force coefficients for the rigid and flexible wings. The highly flexible wings experienced large reductions in the average vertical force as compared to the rigid wings, thus suggesting that adding a high degree of spanwise flexibility to rigid wings could detrimentally affect hovering in small insect flight. For the moderately flexible wings, the results are twofold. When \(Re < 16\), the wings generated a considerably smaller average vertical force than the rigid wings, which is problematic for hovering. But when \(Re > 16\), the moderately flexible wings were nearly as effective as the rigid wings in terms of average vertical force. This result implies that moderately flexible wings produce a nearly equivalent amount of vertical force to rigid wings during hovering flight at \(Re > 16\).
It is worth mentioning that some studies have suggested that flexibility could reduce the energetic requirements of insect flight [4, 8]. For \(Re > 16\), moderately spanwise flexible wings could therefore be more energetically efficient than rigid wings. We encourage a rigorous future investigation to support this very interesting hypothesis.
Conclusions
In this project, we utilized 3D numerical simulations to investigate the way in which wing bristles and wing flexibility affect hovering aerodynamics in the smallest flying insects. Our findings suggest that bristled wings generate nearly as much vertical force as membranous wings during hovering in small insect flight, all while offering the benefit of higher energy efficiency. This result could explain why observational evidence indicates that most tiny insects have highly bristled wings. Knowledge of bristles’ role in tiny insect flight may be of great interest for the design and development of miniature drones. In addition, the improved efficiency from bristles suggests that other organisms that fly/swim at similar \(Re\) might also use them to improve locomotor efficiency. It may even be appropriate to say that bristles are a paradigm of nature’s ingenuity.
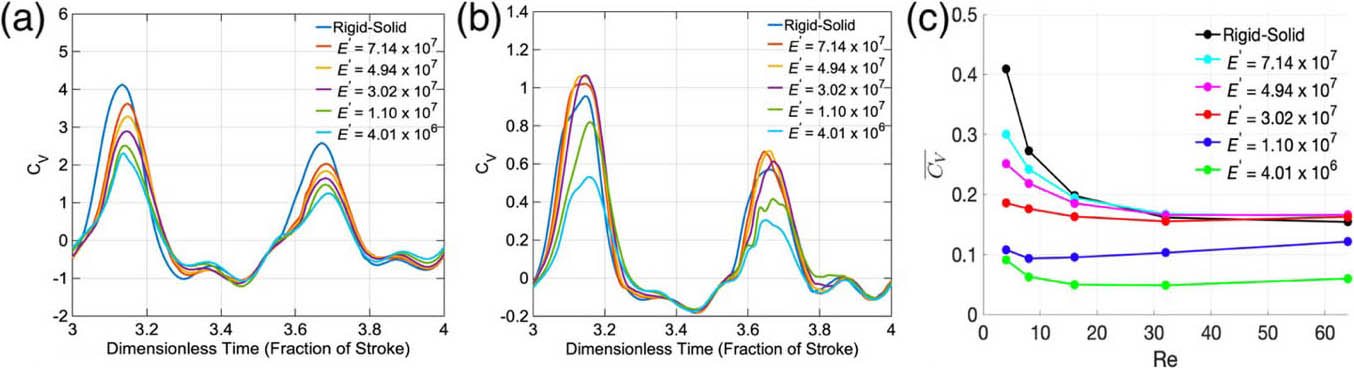
Our most important result for wing flexibility is that for \(Re > 16\), moderately spanwise flexible wings may be as effective as rigid wings during hovering — while also potentially offering the benefit of higher energy efficiency. Therefore, some tiny insects might possess moderately spanwise-flexible wings. Future experimental work that considers the mechanical design of insect wings should consider this feature. In the context of bioinspired design, engineers could use this result to implement moderately spanwise-flexible wings for more energetically efficient micro aerial vehicles. Given the energy constraints that are associated with the operation of tiny drones for long periods of time, this opportunity is important; moderately spanwise-flexible wings could enhance the endurance of these drones.
Research that pertains to small insect flight can offer rich insights into fundamental fluid dynamics and the biomechanics of tiny insects. We encourage extensive work in the future that will further advance our understanding of this fascinating field.
Hrithik Aghav presented this research during a contributed presentation at the 2022 SIAM Annual Meeting, which took place in Pittsburgh, Pa., last summer.
References
[1] Cheng, X., & Sun, M. (2018). Very small insects use novel wing flapping and drag principle to generate the weight-supporting vertical force. J. Fluid Mech., 855, 646-670.
[2] Griffith, B.E., & Luo, X. (2017). Hybrid finite difference/finite element immersed boundary method. Int. J. Numer. Method Biomed. Eng., 33(12), e2888.
[3] Jones, S.K., Laurenza, R., Hedrick, T.L., Griffith, B.E., & Miller, L.A. (2015). Lift vs. drag based mechanisms for vertical force production in the smallest flying insects. J. Theor. Biol., 384, 105-120.
[4] Nguyen, T.A., & Han, J.-H. (2018). Wing flexibility effects on the flight performance of an insect-like-flapping-wing micro-air vehicle. Aerosp. Sci. Technol., 79, 468-481.
[5] Peskin, C.S. (1972). Flow patterns around heart valves: A numerical method. J. Comput. Phys., 10(2), 252-271. i
[6] Peskin, C.S. (1977). Numerical analysis of blood flow in the heart. J. Comput. Phys., 25(3), 220-252.
[7] Peskin, C.S. (2002). The immersed boundary method. Acta Numer., 11, 479-517.
[8] Reid, H.E., Schwab, R.K., Maxcer, M., Peterson, K.D.P., Johnson, E.L., & Jankauski, M. (2019). Wing flexibility reduces the energetic requirements of insect flight. Bioinspir. Biomim., 14(5), 056007.
About the Authors
Hrithik Aghav
Student, University of Arizona
Hrithik Aghav is an undergraduate student at the University of Arizona with a major in mathematics and minor in aerospace engineering. His research interests are insect flight aerodynamics and boundary layer transitions.
Laura A. Miller
Professor, University of Arizona
Laura A. Miller is a professor at the University of Arizona Department of Mathematics with an adjunct appointment in the Department of Biomedical Engineering. Her research studies the fluid dynamics of animals and plans using high-fidelity numerical simulations and experiments.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



