From a Point to a Torus: Unveiling Emergent Dynamics with Higher-order Bifurcations
Bifurcation theory describes qualitative changes in the solutions of dynamical systems as parameters vary. The theory’s origins date back to Henri Poincaré, who foresaw the potential for complexity when stable and unstable manifolds intersect transversally [1, 5]. Many other mathematicians have since contributed to the systematic classification of bifurcations [1, 6]. This classification is aided by consideration of the bifurcation’s codimension, which is the number of parameters that must be varied for the bifurcation to be observable. Only two generic codimension-one bifurcations of fixed points exist for continuous-time dynamics: saddle-node and Andronov-Hopf bifurcations. Likewise, there are three generic codimension-one bifurcations of limit cycles: saddle-node, period-doubling, and torus bifurcations.
Despite longstanding interest in the field, research continues to reveal new bifurcation phenomena. Bifurcations that are associated with higher codimensions, higher-dimensional invariant sets, and global topological changes are prominent research subjects — as is the analysis of higher-order bifurcations, which occur with the vanishing of leading-order terms in a local expansion. Another important line of inquiry concerns system symmetries, which can guarantee conditions that would otherwise be nongeneric and lower the codimension of higher-order bifurcations [4]. Common codimension-one examples include pitchfork and transcritical bifurcations of fixed points — though other important, less-studied cases exist as well. The ongoing classification of these higher-order bifurcations reveals new insights into emergent phenomena, such as self-organized criticality [11] and the formation of localized states [2]. Our recent work analyzes intriguing higher-order bifurcations to understand novel symmetry phenomena in networks of coupled oscillators [7-10].
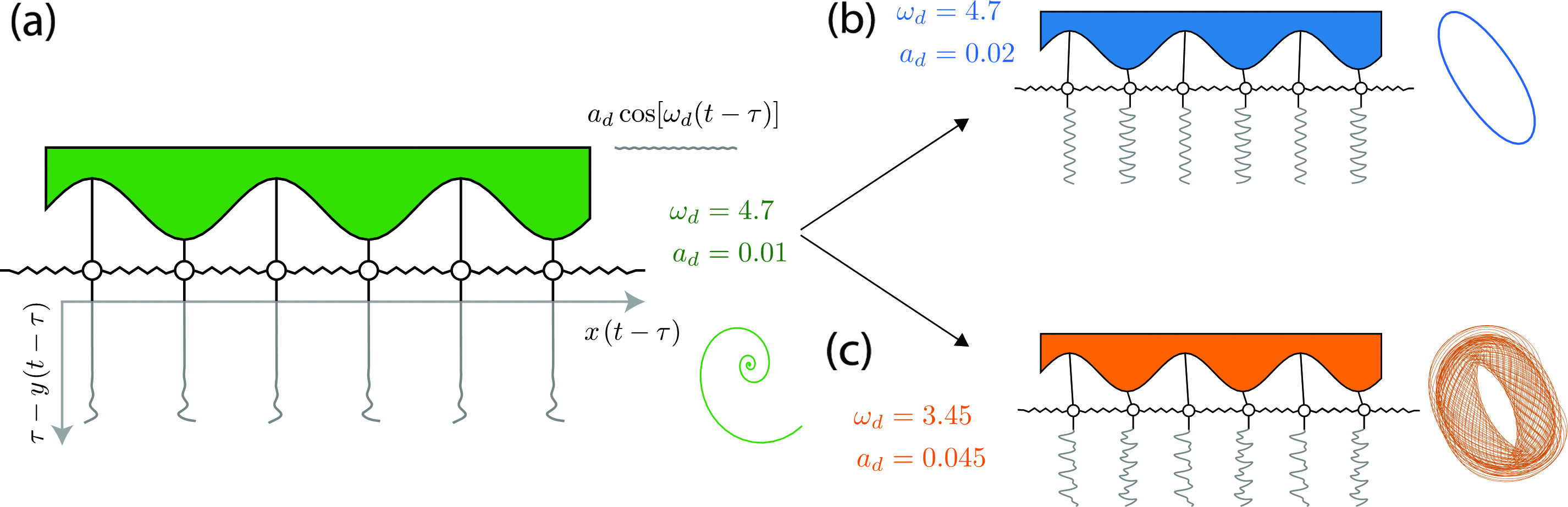
The bifurcations in a vibration-driven array of pendulums with alternating lengths serve as one such example (see Figure 1) [8, 10]. The dynamics of this system are governed by
\[\ddot{\theta}_i=-0.1 \dot{\theta}_i-\frac{1+(-1)^i4\Delta+a_d\omega^2_d\cos(\omega_dt)}{1-(-1)^i\Delta}\sin(\theta_i)+ \frac{1+(-1)^i\Delta}{1-(-1)^i\Delta}[\sin(\theta_{i+1}-\theta_i)+\sin(\theta_{i-1}-\theta_i)], \tag1\]
where \(\theta_i\) is the angle of the \(i\)th pendulum with respect to the vertical direction, \(a_d\) is the driving amplitude, \(\omega_d\) is the driving frequency, and \(\Delta\) is the alternating offset length. The attracting state for a small driving amplitude corresponds to all pendulums in the vertical position (see Figure 1a). This steady state’s stability is determined by the Floquet multipliers of the stroboscopic map between consecutive driving periods. For an increasing driving amplitude \(a_d\), one might expect (based on previous studies of Faraday waves) that the pendulums will respond in a subharmonic fashion and oscillate at half the driving frequency, ultimately forming a limit cycle. Such a response does indeed occur for a range of driving frequencies (see Figure 1b). However, for other driving frequencies, the first bifurcation that the system encounters is a direct transition from a fixed point to an invariant torus (see Figure 1c) [10]. We can interpret the latter as a continuous form of a Neimark-Sacker bifurcation, not to be confused with the torus bifurcation (i.e., the torus’ emergence from a limit cycle). For the system in \((1)\), this counterintuitive bifurcation yields an anharmonic response in which the pendulums oscillate at frequencies that are incommensurate with the driving frequency \(\omega_d\) (see Animation 1).
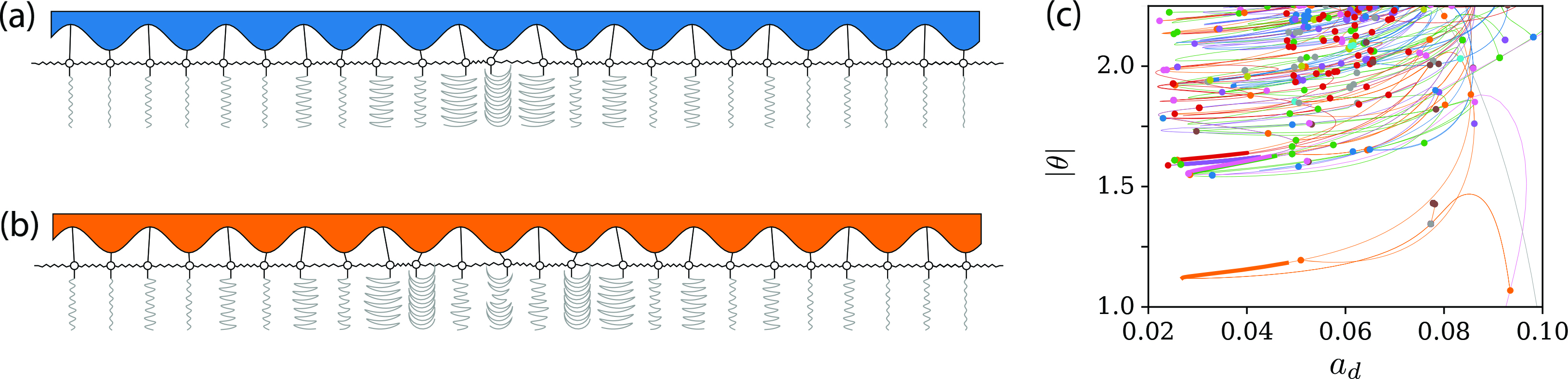
From a symmetry perspective, the alternating structure of the pendulum lengths partially breaks the translational symmetry, which manifests as a band gap in the dispersion relation between the wave modes’ frequencies and the wavelengths for the corresponding undriven system. The anharmonic response occurs precisely when the system is driven at frequencies within this band gap [10], which suppresses the usual subharmonic response. The underlying mechanism is a coresonance—wherein two wave modes mix in order to resonate with the driving frequency—that happens when the frequencies of the wave modes differ by an integer multiple of the driving frequency. Since this condition is typically satisfied when the individual wave mode frequencies are incommensurate with the driving, it provides a simple criterion for the driving frequencies — leading to the anharmonic response and the corresponding response frequencies. We can use this criterion to continuously tune the response frequencies by varying the driving frequency. Another consequence of band gaps is the formation of localized states (gap solitons), which arise from secondary bifurcations that themselves emerge from subcritical primary instabilities (see Animation 2) [8]. These secondary bifurcations in the pendulum array—which are pitchfork and transcritical bifurcations—lead to both subharmonic and anharmonic gap solitons (see Figure 2) [7]. The soliton solutions are connected by a complicated tangle of bifurcations that appear to exhibit a fractal structure that depends on the system symmetry.
Recent studies have also emphasized the appearance of novel global bifurcations in systems with symmetries that involve time reversal. For instance, homoclinic orbits are structurally unstable in generic damped-driven systems [6], but they can persist under one-parameter variations in autonomous Hamiltonian systems — which are invariant under time reversal. This phenomenon gives rise to the well-characterized branches of localized steady states in the cubic-quintic Swift-Hohenberg equation that emanate from a Hamiltonian-Hopf bifurcation point [2]. Only recently has the community broadly appreciated the presence of other time-related symmetries in dissipative systems as well, such as parity-time (PT) symmetries in non-Hermitian quantum systems [3]. These symmetries constrain the eigenvalues of invariant fixed points (and the Floquet multipliers of invariant limit cycles) so that they are either imaginary or appear in pairs with opposite real parts. Bifurcation points in such systems can thus correspond to exceptional points, where eigenvectors coalesce as two or more eigenvalues come together on the imaginary axis.
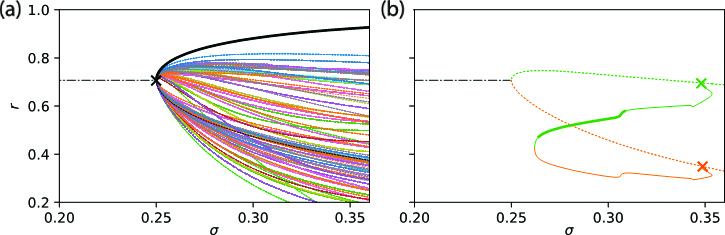
We recently identified related bifurcation phenomena that are governed by PT symmetries in the rings of Janus oscillators [7, 9]. The Janus oscillators are comprised of pairs of detuned Kuramoto oscillators and defined as \(\dot{\theta}_i=\nu_i/2+\beta\sin(\theta_{i + \nu_i}-\theta_i)+\sigma\sin(\theta_{i-\nu_i}-\theta_i)\), where \(\beta\) and \(\sigma\) are coupling constants and \(\nu_i=(-1)^i\); an interactive interface that explores the dynamics of Janus oscillator networks is available online. The rotationally symmetric ring of Janus oscillators exhibits a surprisingly large number of chimera states: patterns of coexisting synchrony and asynchrony [9]. It also exhibits a synchronous state wherein the even and odd oscillators form phase-locked groups that appear via a higher-order bifurcation (see Figure 3a). This bifurcation involves a time-reversal invariant limit cycle whose Floquet multipliers are all neutrally stable [7]. Consequently, multiple unstable steady states emerge from this higher-order bifurcation point. For larger coupling constants, the unstable steady states undergo global bifurcations of heteroclinic cycles (see Figure 3b) that yield the aforementioned chimera states.
More than a century has passed since researchers first attempted to classify bifurcations. During this time, we have seen considerable progress in both the classification of generic bifurcations with low codimension and the recognition of universality as dictated by system symmetry. Advancements have also connected bifurcations with dynamical phenomena in network systems. These efforts will certainly find important applications as researchers continue to strive for greater control of complex systems.
References
[1] Arnol’d, V.I. (Ed.). (1994). Dynamical systems V: Bifurcation theory and catastrophe theory. In Encyclopaedia of mathematical sciences (Vol. 5). Berlin, Germany: Springer-Verlag.
[2] Burke, J., & Knobloch, E. (2006). Localized states in the generalized Swift-Hohenberg equation. Phys. Rev. E, 73(5), 056211.
[3] El-Ganainy, R., Makris, K.G., Khajavikhan, M., Musslimani, Z.H., Rotter, S., & Christodoulides, D.N. (2018). Non-Hermitian physics and PT symmetry. Nat. Phys., 14, 11-19.
[4] Golubitsky, M., Stewart, I., & Schaeffer, D.G. (1988). Singularities and groups in bifurcation theory (Vol. 2). New York, NY: Springer.
[5] Holmes, P. (1990). Poincaré, celestial mechanics, dynamical-systems theory and “chaos.” Phys. Rep., 193(3), 137-163.
[6] Kuznetsov, Y.A. (2004). Elements of applied bifurcation theory (3rd ed.). In Applied mathematical science (Vol. 112). New York, NY: Springer.
[7] Nicolaou, Z.G., & Bramburger, J.J. (2024). Complex localization mechanisms in networks of coupled oscillators: Two case studies. Chaos, 34(1), 013131.
[8] Nicolaou, Z.G., Case, D.J., van der Wee, E.B., Driscoll, M.M., & Motter, A.E. (2021). Heterogeneity-stabilized homogeneous states in driven media. Nat. Commun., 12, 4486.
[9] Nicolaou, Z.G., Eroğlu, D., & Motter, A.E. (2019). Multifaceted dynamics of Janus oscillator networks. Phys. Rev. X, 9(1), 011017.
[10] Nicolaou, Z.G., & Motter, A.E. (2021). Anharmonic classical time crystals: A coresonance pattern formation mechanism. Phys. Rev. Res., 3(2), 023106.
[11] Sormunen, S., Gross, T., & Saramäki, J. (2023). Critical drift in a neuro-inspired adaptive network. Phys. Rev. Lett., 130(18), 188401.
About the Authors
Zachary G. Nicolaou
Washington Research Foundation Postdoctoral Fellow, University of Washington.
Zachary G. Nicolaou is a Washington Research Foundation Postdoctoral Fellow and an acting instructor in the Department of Applied Mathematics at the University of Washington.
Adilson E. Motter
Professor, Northwestern University
Adilson Motter is the Charles E. and Emma H. Morrison Professor of Physics and Astronomy at Northwestern University.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



