Frozen Fingers, Warm Heart: A Predictive Model for Survival Heat Management

Anyone who has tried to zip a jacket on a blustery mountain ridge knows how quickly dexterity disappears when fingers freeze. Yet those distal digits surrender their warmth not by accident, but by design. Hands and feet boast a surface-area-to-mass ratio that is three to five times greater than that of the body; they are able to dissipate up to 220 W m⁻² of thermal energy in hot environments [9]. When temperatures drop, however, the body redirects blood away from these extremities and transforms them from high-surface-area radiators into insulating shells. Indeed, blood perfusion in the hands varies over a staggering 150-fold range — from a maximum rate of 30 milliliters (mL) of blood per 100 mL of tissue per minute when hot, to a minimum of 0.2 mL 100 mL⁻¹ min⁻¹ when cold [9]. In a survival situation, the body forfeits its frozen fingers to keep the core warm.

Here, we present a model of this process that extends a known classical linear model, and mention some forthcoming analyses and numerical experiments [5]; see also our previous work [8].

Background

We can describe energy exchange due to blood perfusion—i.e., fluid flow through the microvasculature in tissue—with Pennes’ bioheat equation [7]:

\[c \rho u_t - \nabla \cdot (k \nabla u) + R \, (u - u_b) = f. \tag1\]

The energy exchange term \(R \, (u - u_b)\) controls the closeness of tissue temperature \(u\) and blood temperature \(u_b\) (see Figure 1). The empirical relationship

\[R = c_b \rho_b \omega_b \tag2\]

provides a direct connection to the blood perfusion rate \(\omega_b\) [7]. 

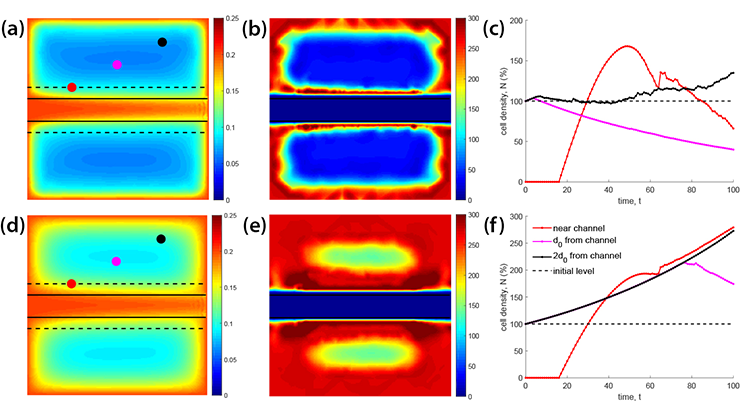
In turn, the authors of [4] derive a stationary version of \((1)\) from “mathematical scratch” as the homogenized limit of microscale Robin boundary value problems (see Figure 2). This limit is

\[-\nabla \cdot (\mathcal{A} \nabla u) + R \, (u - u_b) = \frac{|Y^*|}{|Y|} f,\]

where \(R=a\frac{|\partial Q|}{|Y|}\), \(a\) is the Robin conductance, \(|\partial Q|/|Y|\) is specific surface area of the blood vessels, \(|Y^*| / |Y|\) is the volume fraction of the solid tissue, and \(\mathcal{A}\) is the homogenized diffusion tensor that is standard for such problems.

In our model, \(R = R(u,v)\) depends dynamically on both local tissue temperature \(u\) and body core temperature \(v\). The “body”—and its thermal regulating functions—is represented by a compartmental, zero-dimensional model that dynamically interacts with the temperature of the hand (an extremity). 

Microscale to Macroscale Simulations

Next, we illustrate the effect of \(R \, (u - u_b)\) in \((1)\) as derived by homogenization. Let

\[\Omega = (0,x'_1) \times (0,x'_2),  \quad x'_1 = 0.03, \;\: x'_2 = 0.01\]

represent a three square centimeter (cm) patch of tissue with \(\partial \Omega = \partial \Omega_D \cup \partial \Omega_N\), defined as

\[\begin{eqnarray} \partial \Omega_D \; &:=& \; \{(x_1,x_2) \in \partial \Omega : x_1 = 0 \, \text{ or } \, x_1 = x_1'\}, \\ \partial \Omega_N \; &:=& \; \{(x_1,x_2) \in \partial \Omega : x_2 = 0 \, \text{ or } \, x_2 = x_2'\}. \end{eqnarray}\]

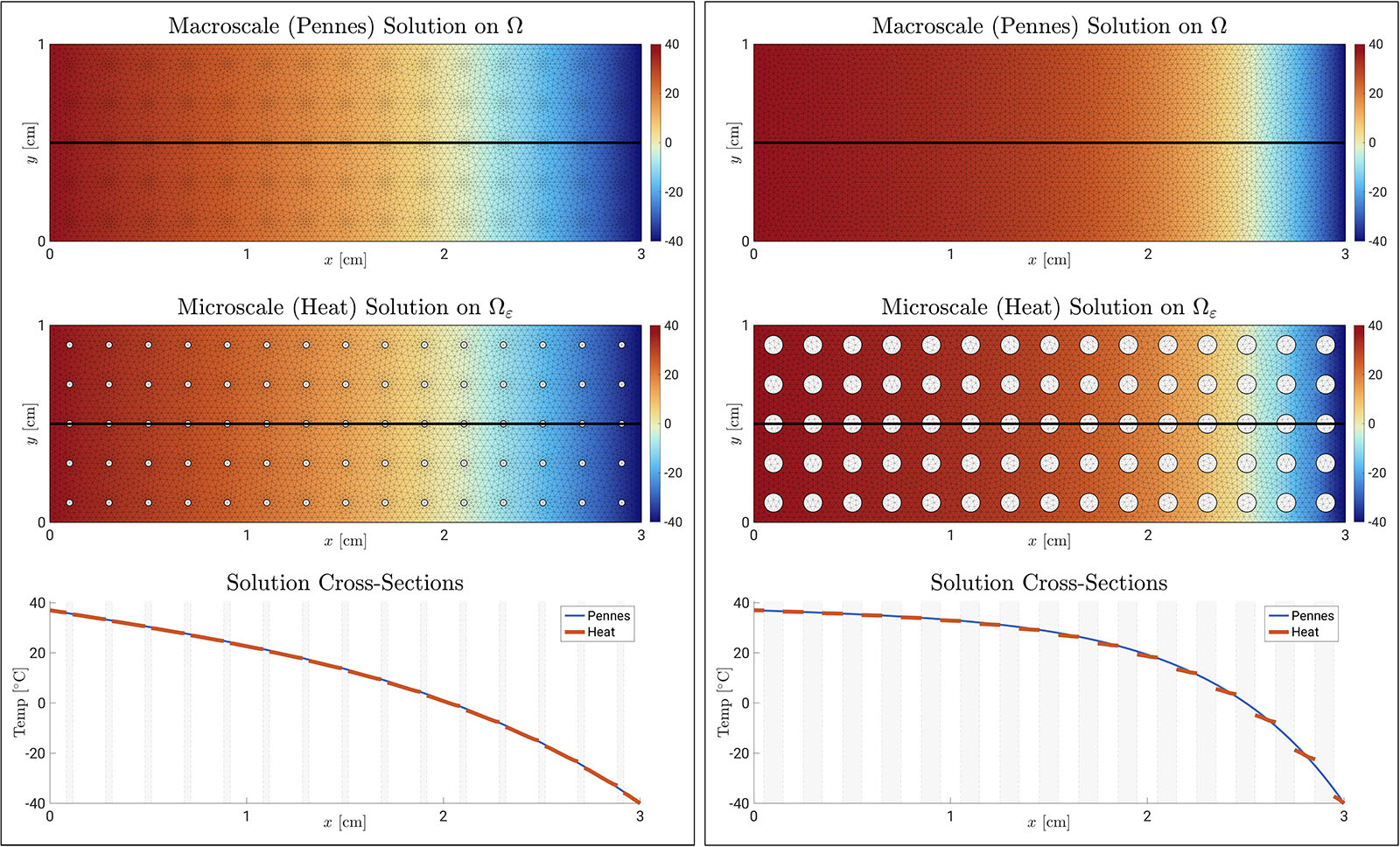
We obtain a perforated domain \(\Omega_\varepsilon\) by periodically excising 75 disk-shaped holes from \(\Omega\) (see Figure 3). Let \(T = 7{,}200\) seconds (s).

To extend the work of [4], we postulate that solutions \(u_\varepsilon\) to microscale problems

\[\begin{eqnarray} (c u_\varepsilon)_t  - \nabla \cdot (k \nabla u_\varepsilon)  &=& f_\varepsilon \qquad \qquad \qquad &\text{in} \enspace \Omega_\varepsilon \times (0,T],& \tag{3a} \\   u_\varepsilon  &=& u_D \qquad \qquad \qquad &\text{on} \enspace \partial \Omega_D \times (0,T],& \tag{3b} \\  \frac{\partial u_\varepsilon}{\partial n}   &=& 0  \qquad \qquad \qquad &\text{on} \enspace \partial \Omega_N \times (0,T],& \tag{3c} \\  -k \frac{\partial u}{\partial n} &=& \varepsilon a (u_\varepsilon - u^\varepsilon_b)  \qquad \qquad \qquad &\text{on} \enspace \partial Q_\varepsilon \times (0,T],& \tag{3d} \\ u_\varepsilon(x,0) &=& u^\varepsilon_\text{init}(x)  \qquad \qquad \qquad &\text{in} \enspace {\Omega_\varepsilon}& \tag{3e} \end{eqnarray}\]

are well approximated by solution \(u\) to the macroscale problem

\[\begin{eqnarray} c \frac{|Y^*|}{|Y|} u_t - \nabla \cdot (k \, \mathcal{A} \, \nabla u) + a \frac{|\partial Q|}{|Y|}(u - u_b)&=& \frac{|Y^*|}{|Y|} f, \qquad \qquad \qquad &\text{in} \enspace \Omega \times (0,T],& \tag{4a} \\ u &=& u_D, \qquad \qquad \qquad &\text{on} \enspace \partial \Omega_D \times (0,T],& \tag{4b} \\ \frac{\partial u}{\partial n} &=& 0, \qquad \qquad \qquad &\text{on} \enspace \partial \Omega_N \times (0,T],& \tag{4c} \\ u(x,0) &=& u_\text{init}(x), \qquad \qquad \qquad &\text{in} \enspace \Omega,& \tag{4d} \end{eqnarray}\]

where \(n\) is an outward normal vector.

To illustrate this concept numerically, we discretize \((3)\) and \((4)\) using P1 Lagrange finite elements (mesh size \(h=2^{-6}\) cm) and backward Euler time stepping (time step \(\tau = 1\) s). This scenario simulates tissue \(\Omega\) that touches a cold object (\(u = -40^\circ\) Celsius (C)) on its east edge while connected to the body’s core (\(u = 37^\circ\) C) on its west edge. The tissue is warmed by perfusing blood (\(u_b = 37^\circ\) C) via either the Robin condition in \((3\textrm{d})\) or the homogenized energy exchange term \(a |\partial Q| / |Y| \, (u - u_b)\) in \((4\textrm{a})\). We use coefficients from Figure 1 and set \(u^\varepsilon_b=u_b\), \(u_\textrm{init}=u_b\), \(u^\varepsilon_{\textrm{init}}=u_b\), \(a=\rho_bc_b\omega_b\), and

\[u_D=\begin{cases} u_b, \qquad \, x_1=0, \\ u_\textrm{cold}, \quad \; x_1=x'_1. \end{cases}\]

We plot the solutions in Figure 3, observing close agreement between \(u\) and \(u_\varepsilon\) on \(\Omega_\varepsilon\) for all \(n \tau \in (0,T]\). Moreover, increasing the perforation size from \(|\partial Q| / |Y| = 0.5\) to \(|\partial Q| / |Y| = 1.5\) raises the average temperature \(\langle u(t) \rangle_{\Omega_\varepsilon}\).

New Model

Now, we will overview the main elements of our model that aims to describe the dynamics of energy exchange between an extremity and the body’s core over time \(t \in (0,T]\).

Let domain \(\Omega\) represent the hand (see Figure 4). We seek temperature \(u: \Omega \times (0,T] \to \mathbb{R}\) and temperature \(v: (0,T] \to \mathbb{R}\) in the “body” (a zero-dimensional compartment) that satisfy

\[\begin{eqnarray}  c \rho u_t - \nabla \cdot (k \nabla u) + R(u,v) \, (u - v) \enspace &=& \enspace f, \quad \text{in} \enspace \Omega \times (0,T], \tag{5a} \\  - k \frac{\partial u}{\partial n} \enspace &=& \enspace \alpha(u - u_\text{cold}),  \quad \text{on} \enspace \partial \Omega_\text{air} \times (0,T], \tag{5b} \\ - k \frac{\partial u}{\partial n} \enspace &=& \enspace \alpha(u - v), \quad \text{on} \enspace \partial \Omega_\text{wrist} \times (0,T], \tag {5c} \\ u(x,0) \enspace &=& \enspace u_\text{init}, \quad \text{in} \enspace \Omega, \tag{5d} \end{eqnarray}\]

and

\[\begin{eqnarray} \kappa \frac{dv}{dt} + S(v, \langle u \rangle_\Omega) \, (v - \langle u \rangle_\Omega) \enspace &=& \enspace g, \quad t \in (0,T], \tag{6a} \\ v(0) \enspace &=& \enspace v_\text{init}. \tag{6b} \end{eqnarray}\]

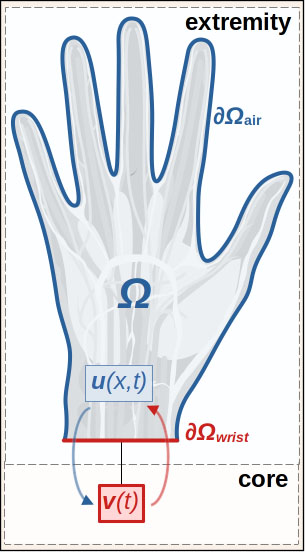
In this model, we replace constant \(R\) with \(R = R(u,v)\), which we postulate is given by

\[R(u,v) = A \, \sigma_1(u) \,\sigma_2(v). \tag7\]

Here, \(A = c_b \rho_b \omega_b\) and \(\sigma_i: \mathbb{R} \to [0,1]\), \(i \in \{1,2\}\) are ramp functions whose breakpoints correspond to physiologically defined thresholds \(u_L, u_R\) and \(v_L, v_R\) (see Figure 5).

We designed our heuristic model to capture the body’s independent local and systemic blood flow regulation mechanisms that respectively respond to changes in local or core temperature [1]. If \(u(x,t) < u_R\) at some \(x \in \Omega\), exchange is diminished near \(x\); if \(v(t) < v_R\), exchange is suppressed throughout \(\Omega\). However, the model reduces to \((1)\) with \(R\) from \((2)\) when \(u(\cdot,t) > u_R\) and \(v(t) > v_R\).

In turn, \(S(v,\langle u\rangle_\Omega)(v-\langle u\rangle_\Omega)\) in \((6)\) uses average hand temperature \(\langle u \rangle_\Omega\) to approximate the temperature of the blood that returns to the body from the hand. We postulate that reduced warm blood flow from core to hand corresponds to reduced cooled return flow, motivating

\[S(v, \langle u \rangle_\Omega) = B \, \sigma_1(\langle u \rangle_\Omega) \, \sigma_2(v). \tag8\]

Here, \(B = 0.07 A\) since the hand contains roughly seven percent of total blood volume [9].

Discrete Scheme, Stability, and Convergence

We now mention some forthcoming analysis of our numerical approximation of the nonlinear model [5]. In particular, we prove a product-space stability estimate; under affine growth assumptions on the data in \((5)\) and \((6)\), the energy

\[E(t) := \tfrac12\bigl(\|u(\cdot,t)\|_{L^2(\Omega)}^2 + |v(t)|^2\bigr), \quad 0 \le t \le T\]

has bound

\[E(t) \leq e^{A t}\Bigl[E(0) + C\,t + \int_0^t\bigl(\|f(s)\|_{L^2(\Omega)}^2 + |g(s)|^2\bigr)\,ds\Bigr], \tag9\]

where constants \(A\) and \(C\) depend only on problem data. From \((9)\), we also show a bound on \(|dv / dt|\). 

After discretizing \((5)\) and \((6)\) via P1 Galerkin finite elements (with mesh size \(h\)) and backward Euler time stepping (time step \(\tau\)) so that \(U^n \approx u(\cdot, t^n)\) and \(V^n \approx v(t^n)\) where \(t^n := n \tau\), we can prove that discrete energy

\[E^n := \tfrac{1}{2}(\|U^n\|_{L^2(\Omega)}^2 + |V^n|^2)\]

remains uniformly bounded in \(n\), given mild restrictions on time step \(\tau\). Assuming that the data in \((5)\) and \((6)\) are Lipschitz, we also show that the fully discrete solution converges optimally in the product norm: 

\[\max_{0 \leq n \leq N} (\|u(\cdot,t_n) - U^n\|_{L^2(\Omega)} + |v(t_n) - V^n| ) \leq C \, (h^2 + \tau),\]

where \(C\) is independent of \(h\) and \(\tau\).

Illustration of the Model

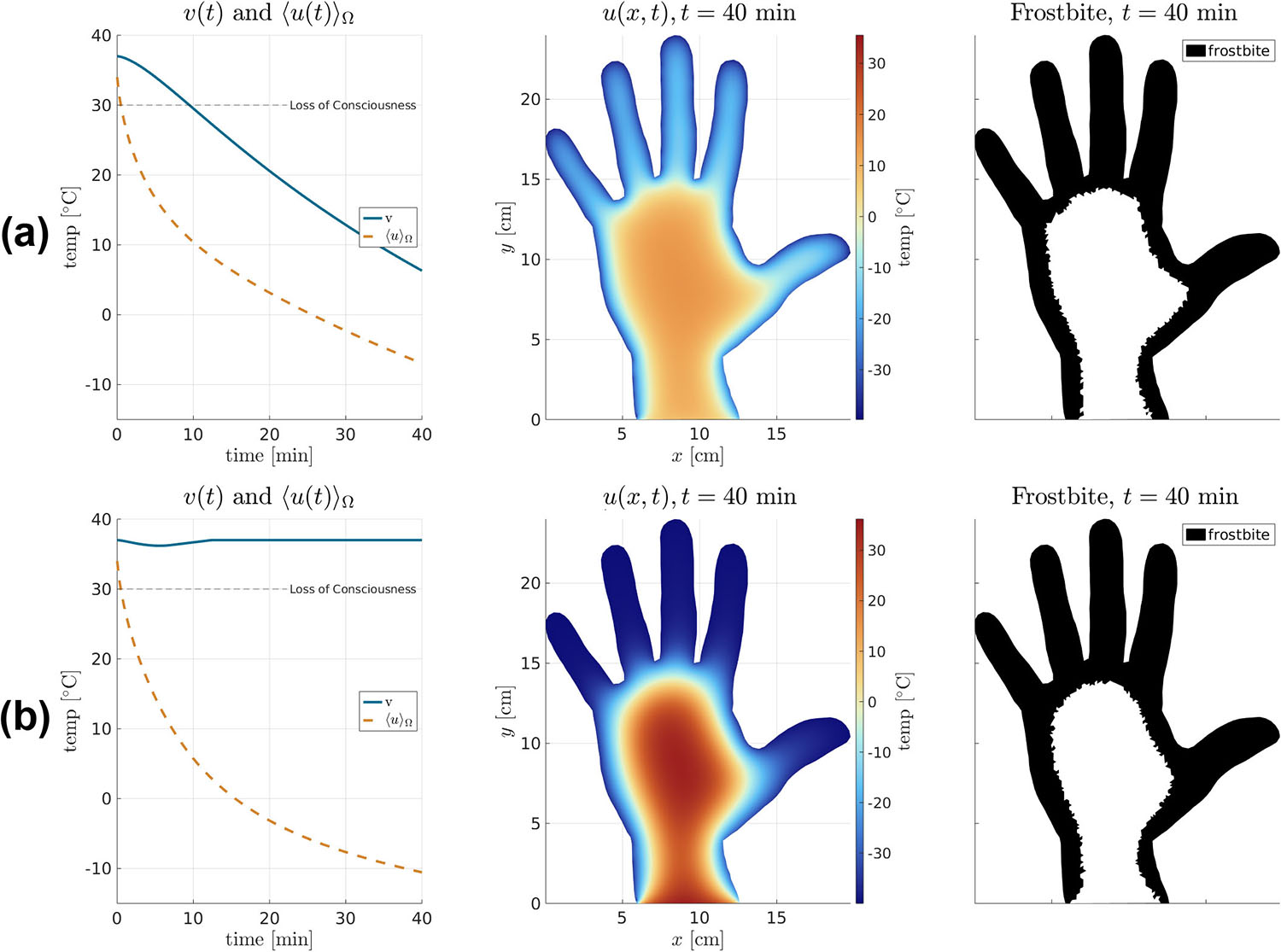
To illustrate our model via simulation, consider the scenario of a climber in \(u_\text{cold} = -40^\circ\) C who attempts self-rescue after losing a glove. We set \(u_\text{init} = 34\), \(v_\text{init} = 37\), and metabolic rate \(g=800\) W m⁻³, which is consistent with extensive shivering combined with moderate physical activity [2]. In this scenario, frostbite (i.e., \(u < 0\)) will begin within minutes [3], but the core body temperature should remain in a survivable range. We simulate two cases:

• \((\text{L})\): constant \(R=A\) and \(S=B\) (linear model with no dynamic control)
• \((\text{N})\): nonlinear \(R\) and \(S\) as in \((7)\) and \((8)\) (dynamic coupling).

Figure 6 illustrates the role of nonlinear coupling in \((7)\) and \((8)\). In \((\text{L})\), heat flows unimpeded from core to hand to air, so both \(\langle u \rangle_\Omega\) and \(v\) decay toward \(u_\text{cold}\). In \((\text{N})\), an initial drop in \(v\) throttles energy exchange, allowing metabolism to recover core temperature but causing deeper frostbite and lower \(\langle u \rangle_\Omega\); this mechanism agrees with physiological observations.

Concluding Thoughts

Based on our initial analyses and simulations, we believe that our heuristic model provides a reasonable mechanistic view of extremity-core heat transfer in cold stress. There is also potential to extend the model and analysis. Because our theoretical results apply to general Lipschitz terms \(R(u,v),S(v,\langle u \rangle_\Omega)\) and nonlinear boundary conditions [5], they provide the opportunity to postulate and test other models for situations such as hyperthermia or radiation boundary conditions. Additionally, we could consider more compartments and tissue types and incorporate a bona fide hypothalamic-sympathetic feedback loop.

---

Tyler Fara delivered a contributed presentation on this research at the 2024 SIAM Annual Meeting (AN24), which took place last year in Spokane, Wash. He received funding to attend AN24 through a SIAM Student Travel Award. To learn more about Student Travel Awards and submit an application, visit the online page.

SIAM Student Travel Awards are made possible in part by the generous support of our community. To make a gift to the Student Travel Fund, visit the SIAM website.

Acknowledgments: This research was partially supported by U.S. National Science Foundation grants DMS-2309682 and DMS-1912938 under principal investigator Malgorzata Peszynska of Oregon State University.

References
[1] Alba, B.K., Castellani, J.W., & Charkoudian, N. (2019). Cold-induced cutaneous vasoconstriction in humans: Function, dysfunction and the distinctly counterproductive. Exp. Physiol., 104(8), 1202-1214.
[2] Boron, W.F., & Boulpaep, E.L. (2012). Medical physiology: A cellular and molecular approach (2nd ed.) Philadelphia, PA: Elsevier.
[3] Collins, K.J. (1983). Hypothermia: The facts. New York, NY: Oxford University Press.
[4] Deuflhard, P., & Hochmuth, R. (2004). Multiscale analysis of thermoregulation in the human microvascular system. Math. Methods Appl. Sci., 27(8),971-989.
[5] Fara, T., & Peszynska, M. (2025). Nonlinear bioheat model for dynamics of hypothermia and frostbite. Stability analysis and finite element discretization. To be submitted.
[6] Hasgall, P.A., Di Gennaro, F., Baumgartner, C., Neufeld, E., Lloyd, B., Gosselin, M.C., … Kuster, N. (2022). IT’IS database for thermal and electromagnetic parameters of biological tissues, version 4.1. Retrieved from https://itis.swiss/virtual-population/tissue-properties/traceability/doi-v4-0.
[7] Pennes, H.H. (1948). Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol., 1(2), 93-122.
[8] Peszynska, M., Fara, T., Phelps, M., & Zhang, N. (2023). Mixed dimensional modeling with overlapping continua on cartesian grids for complex applications. In E. Franck, J. Fuhrmann, V. Michel-Dansac, & L. Navoret (Eds.), Finite volumes for complex applications X: Elliptic and parabolic problems (Vol. 1) (pp. 129-145). New York, NY: Springer.
[9] Taylor, N.A.S., Machado-Moreira, C.A., van den Heuvel, A.M.J., & Caldwell, J.N. (2014). Hands and feet: Physiological insulators, radiators and evaporators. Eur. J. Appl. Physiol., 114(10), 2037-2060.