Generalized Hypergraph Cut Algorithms and Their Applications

In graph theory, “cuts” are sets of edges whose removal partitions a graph into disconnected clusters. One of the most fundamental cut problems is finding a minimum \(s\)-\(t\) cut, which separates two special nodes \(s\) and \(t\) into different clusters while minimizing the number of edges between these clusters. Polynomial-time solutions for this problem (and its dual, the maximum \(s\)-\(t\) flow problem) date back to the 1950s, and the search for increasingly faster algorithms still continues today. Researchers frequently use minimum \(s\)-\(t\) cut algorithms as subroutines for other graph problems and apply them to tasks like image segmentation, data clustering, and community detection in social networks.

2023 marks the 50th anniversary of Eugene Lawler’s proof that a hypergraph minimum \(s\)-\(t\) cut problem is also polynomial-time solvable [2]. In hypergraphs, nodes are organized into hyperedges that contain an arbitrary number of nodes and are useful for modeling multiway relationships. The hypergraph minimum \(s\)-\(t\) cut problem aims to separate special nodes \(s\) and \(t\) while minimizing a hypergraph cut penalty. But what constitutes a hypergraph cut penalty? When it comes to graphs, the only way to cut an edge is to separate its two nodes into different clusters. However, there are many ways to partition a hyperedge’s nodes across two clusters. Lawler’s algorithm applies to the standard hypergraph cut penalty, which simply counts the number of hyperedges that are cut (i.e., that span both clusters).

The standard hypergraph cut penalty arises naturally in a variety of settings, but there are also multiple applications where certain ways of cutting a hyperedge are more desirable than others [3, 4]. My colleagues and I recently revisited the hypergraph \(s\)-\(t\) cut problem with a renewed interest in what it means—in both theory and practice—to cut a hyperedge [8]. We found that even a seemingly minor generalization of the standard hypergraph cut penalty yields a rich space of theoretical questions, complexity results, and algorithmic primitives for many applications in hypergraph-based data analysis.

The Cardinality-based \(s\)-\(t\) Cut Problem

A natural generalization of Lawler’s hypergraph \(s\)-\(t\) cut problem is to penalize hyperedges based on the number of nodes in each cluster. For the hypergraph in Figure 1, we can assign a penalty of \(w_1 = 1\) for each hyperedge that places exactly one of its nodes in one of the clusters, and another penalty \(w_2 \geq 0\) when exactly two of its nodes are in each cluster. The optimal partition then depends on \(w_2\).

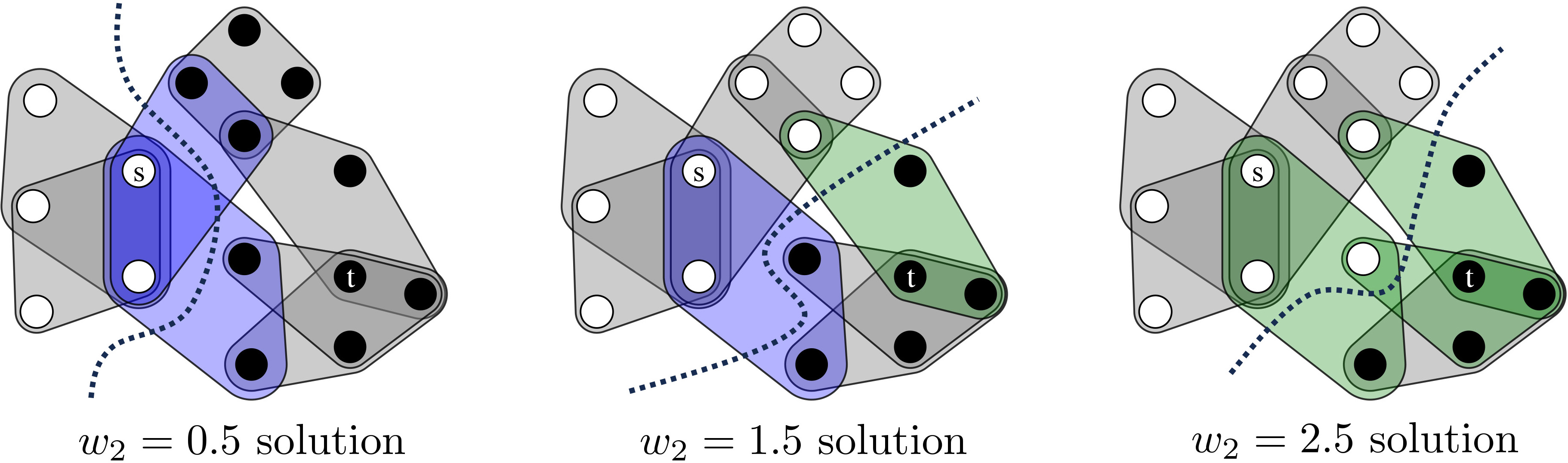
We formalized this idea as the cardinality-based \(s\)-\(t\) cut problem [8]. For a simplified exposition, let us assume that the input hypergraph \(H = (V,E)\) is \(k\)-uniform—meaning that each hyperedge has exactly \(k\) nodes—and that the same type of generalized cut penalty is applied to every hyperedge. These assumptions simplify the explanation without fundamentally altering the results; the analysis easily extends to settings with hyperedges that vary in size and cut penalties. The cardinality-based \(s\)-\(t\) cut problem is

\[\min_{S \subseteq V} \quad \textbf{cut}(S) = \sum_{i = 1}^{\lfloor k/2 \rfloor} w_i \cdot |\partial_i(S)|,\]

subject to \(s \in S\) and \(t \notin S\). Here, \(\partial_i(S) = \{ e \in E \colon \min \{|e \cap S|, |e \cap V\backslash S |\} = i\}\) is the set of hyperedges with exactly \(i\) nodes in one of the clusters \(S \subseteq V\) and \(V \backslash S\), and \(w_i \geq 0\) is the penalty for cutting a hyperedge in this manner. Without loss of generality, penalties are scaled so that \(w_1 = 1\).

Lawler’s work demonstrates that this problem is polynomial-time solvable if \(w_i = 1\) for all \(i \geq 1\) [2], but are other parameter settings amenable to efficient algorithms? Is the problem ever computationally intractable? Such questions are closely tied to motivating applications and practical considerations. Researchers have already employed many types of cardinality-based hypergraph cut penalties (even if they were not explicitly identified as such) in previous hypergraph partitioning applications [8]. Understanding the complexity of the cardinality-based \(s\)-\(t\) cut problem will help us establish rigorous theoretical foundations and algorithmic primitives for these and other downstream applications.

To explore these topics, we turned to a familiar strategy in hypergraph analysis: replace each hyperedge with a small graph gadget, which is defined by a new edge set and potentially new auxiliary nodes. This strategy produces a graph cut problem that is solvable with existing algorithms. Arguably the most common approach is to replace each hyperedge with a clique (see Figure 2b). Another common technique is to replace each hyperedge with a star that is centered at a new auxiliary node (see Figure 2c). Researchers often use clique and star gadgets as simple heuristics for hypergraph analysis or as a means of approximating the standard hypergraph cut penalty. However, we can also view them as a way to exactly model specific cardinality-based cut penalties. Applying clique gadgets to a \(k\)-uniform hypergraph and solving a graph \(s\)-\(t\) cut problem is equivalent to solving the cardinality-based \(s\)-\(t\) cut problem when \(w_i = i \cdot (k-i)\). Meanwhile, the star gadget exactly models the penalty \(w_i = \min\{ i, k - i\}\). Lawler’s hypergraph \(s\)-\(t\) cut algorithm relies on an alternative gadget that models the standard hyperedge cut penalty (see Figure 2d).

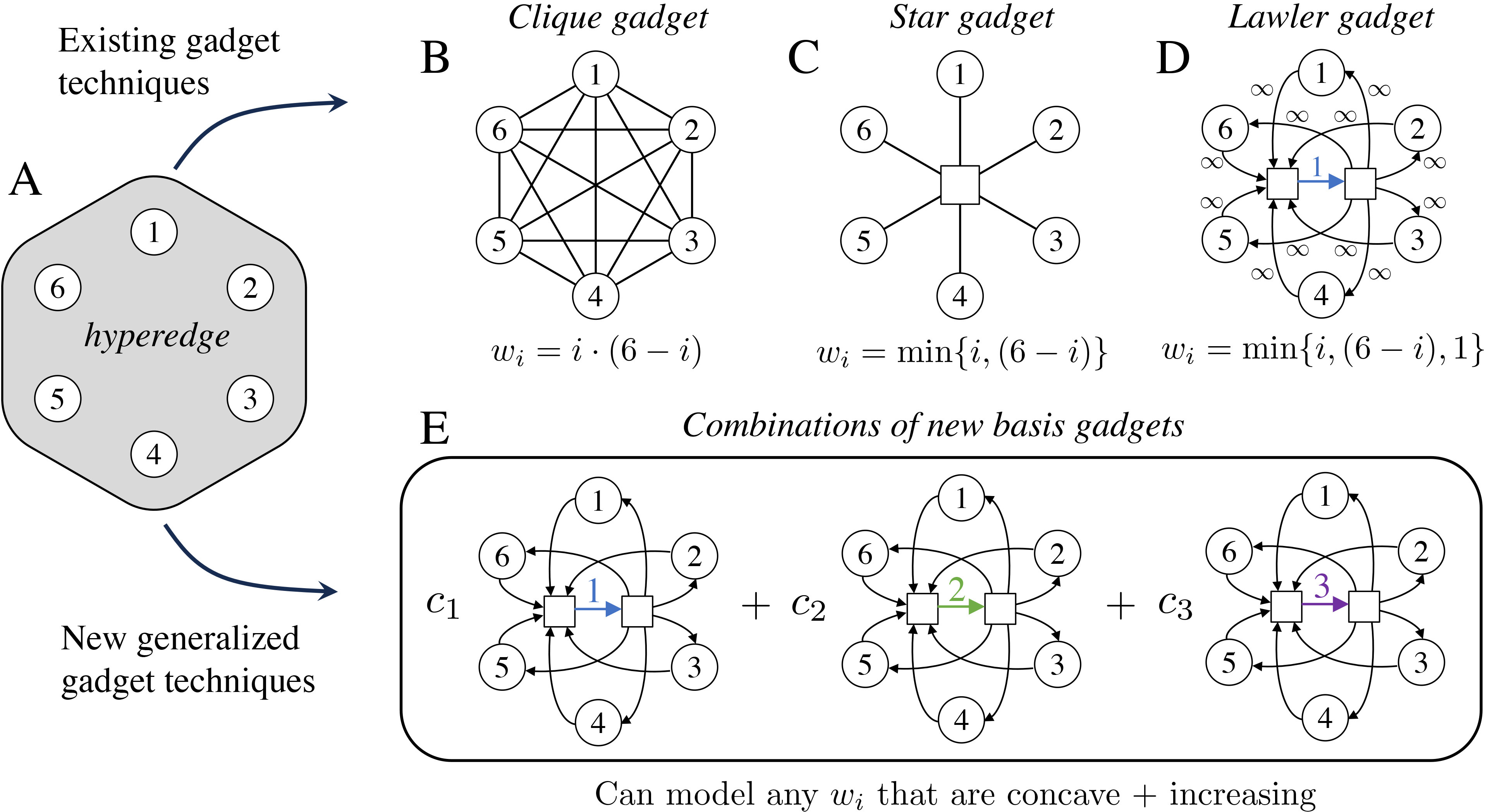
How do we know when we can model a set of cut penalties with such a gadget? We discovered a simple sufficient and necessary condition: a set of cardinality-based penalties can be modeled by a gadget if and only if they are represented by a submodular function. Formalizing this condition requires additional mathematical notation for encoding cut penalties as a set function; informally, the condition means that the sequence of values \(\{w_1, w_2, w_3, \dots\}\) follows an increasing concave curve. We can always represent cut penalties that satisfy this condition with a positive linear combination of newly-defined basis gadgets (see Figure 2e), where the coefficients are obtained by solving a small linear system.

What if this condition is not satisfied? In the case of four-uniform hypergraphs, we can model cut penalties with gadgets as long as \(w_2 \in [1,2]\). However, we proved that the problem is NP-hard when \(w_2 \in [0,1)\). When \(w_2 > 2\), we know that gadget techniques fail, but the complexity of the problem remains unknown in this parameter regime. Figure 1 illustrates the problem’s theoretical richness; although the three cut problems in this figure are fundamentally different in terms of algorithms and complexity, they are distinguished only by a (seemingly) minor change to one cut penalty. For hyperedges with more than four nodes, we proved NP-hardness results for several broader parameter regimes and highlighted broader regimes in which the complexity remains unknown.

Applications in Hypergraph-based Data Analysis

Our results contribute to broader research efforts on generalized hypergraph cut problems that are particularly motivated by recent data science applications. Just as graph \(s\)-\(t\) cut algorithms are often used as subroutines for other graph problems and applications, our hypergraph \(s\)-\(t\) cut algorithms can be directly incorporated into many frameworks for hypergraph clustering and partitioning.

We integrated our gadget techniques and \(s\)-\(t\) cut subroutines into new algorithms for finding localized clusters in large hypergraphs [5, 7]. In practice, cardinality-based cuts led to improvements in detecting clusters of posts on Stack Overflow with the same topic tag (e.g., Python or Verilog) in a hypergraph whose hyperedges represent sets of questions that were answered by the same user. We also used our algorithms to detect clusters of same-category retail products (e.g., fashion or software merchandise) in a hypergraph whose hyperedges indicate sets of co-reviewed Amazon products.

We later used cardinality-based \(s\)-\(t\) cut subroutines to develop faster approximation algorithms for global ratio cut objectives, which seek to minimize the ratio between a generalized hypergraph cut penalty and the resulting cluster’s size [6]. Earlier research revealed that incorporating generalized cut penalties into ratio cut objectives benefits downstream hypergraph-based classification tasks where hyperedges represent sets of data objects that share a categorical feature (e.g., a group of news articles that use the same rare word) [4]. In these settings, a hyperedge provides imperfect but useful evidence that a group of data objects should be classified similarly. We can choose cardinality-based cut penalties that favor clustering most of these data objects together, even if the hyperedge is cut.

We also developed faster approximate solvers for cardinality-based cut problems by replacing hyperedges with new sparse gadgets [9]. This technique led to faster approximate solutions for image segmentation tasks where a hyperedge represents a superpixel: a group of pixels in the same region of an image that share similar pixel intensities and often belong to the same object in the image. We can use cardinality-based cuts to encourage most nodes of a superpixel to cluster together, without placing an excessively high penalty on separating a few pixels from the rest.

Numerous questions remain open for the cardinality-based \(s\)-\(t\) cut problem, such as settling the problem’s complexity in all parameter regimes and developing approximation techniques for NP-hard cases. The cardinality-based \(s\)-\(t\) cut problem is also just one direction within a broader research thrust on generalized hypergraph cut problems. Many recent advances in this area relate to other hypergraph cut objectives and generalized cut penalties that extend beyond cardinality-based cuts [1, 3, 4, 10]. There are a lot of exciting opportunities for further exploration, in terms of both open mathematical questions and new ways to leverage existing techniques for emerging applications where complex, multiway interactions play a central role.

Nate Veldt received the 2023 SIAM Activity Group on Applied and Computational Discrete Algorithms Early Career Prize. He presented the corresponding prize lecture on his work with hypergraphs at the 2023 SIAM Conference on Applied and Computational Discrete Algorithms, which took place earlier this year in Seattle, Wash.

References

[1] Fountoulakis, K., Li, P., & Yang, S. (2021). Local hyper-flow diffusion. In Advances in neural information processing systems 34 (NeurIPS 2021) (pp. 27683-27694). Curran Associates, Inc.
[2] Lawler, E.L. (1973). Cutsets and partitions of hypergraphs. Networks, 3(3), 275-285.
[3] Li, P., & Milenkovic, O. (2017). Inhomogeneous hypergraph clustering with applications. In Advances in neural information processing systems 31 (NeurIPS 2017). Long Beach, CA: Curran Associates, Inc.
[4] Li, P., & Milenkovic, O. (2018). Submodular hypergraphs: p-Laplacians, cheeger inequalities and spectral clustering. In Proceedings of the 35th international conference on machine learning (ICML 2018) (pp. 3014-3023). Stockholm, Sweden.
[5] Liu, M., Veldt, N., Song, H., Li, P., & Gleich, D.F. (2021). Strongly local hypergraph diffusions for clustering and semi-supervised learning. In Proceedings of the web conference 2021 (WWW 2021) (pp. 2092-2103). Association for Computing Machinery.
[6] Veldt, N. (2023). Cut-matching games for generalized hypergraph ratio cuts. In Proceedings of the ACM web conference 2023 (WWW 2023) (pp. 694-704). Austin, TX: Association for Computing Machinery.
[7] Veldt, N., Benson, A.R., & Kleinberg, J. (2020). Minimizing localized ratio cut objectives in hypergraphs. In KDD’20: Proceedings of the 26th ACM SIGKDD international conference on knowledge discovery and data mining (pp. 1708-1718). Association for Computing Machinery.
[8] Veldt, N., Benson, A.R., & Kleinberg, J. (2022). Hypergraph cuts with general splitting functions. SIAM Rev., 64(3), 650-685.
[9] Veldt, N., Benson, A.R., & Kleinberg, J. (2023). Augmented sparsifiers for generalized hypergraph cuts. J. Mach. Learn. Res., 24(207), 1-50.
[10] Zhu, Y., & Segarra, S. (2022). Hypergraph cuts with edge-dependent vertex weights. Appl. Netw. Sci., 7(1), 45.