Geometric Sum, Geometrically

It is customary to prove the geometric sum formula

\[1+ \lambda + \lambda ^2 + \ldots + \lambda ^{n-1} = \frac{1- \lambda ^{n }}{1- \lambda }\tag1\]

by algebra. But a geometric sum deserves a geometric treatment, so here are some geometrical proofs.

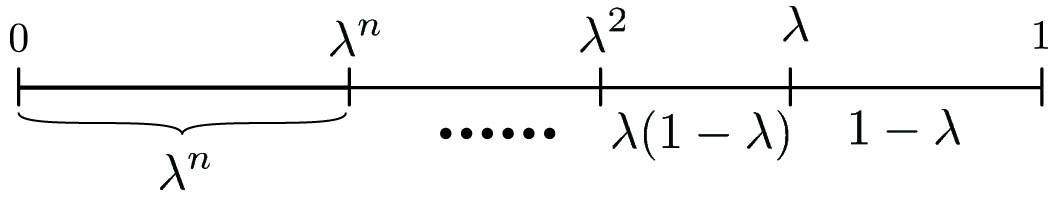
Proof by Dilation

Let us subject the segment \([0,1]\) to a linear dilation \(x\mapsto \lambda x\) that is repeated \(n\) times—as shown in Figure 1—for positive \(\lambda <1\). The iterates \(\lambda,  \ldots, \lambda ^n\) break \([0,1]\) into \(n+1\) subintervals. And the iterates of the rightmost interval \([\lambda, 1]\) have geometrically decreasing lengths \(\lambda ^i(1- \lambda )\) with \(i=0, \ldots, n-1\), as Figure 1 shows. The combined length of all the intervals, recording from right to left in the figure, is 1:

\[(1-\lambda ) + \lambda (1-\lambda ) + \ldots +\lambda ^{n-1} (1-\lambda ) + \lambda ^n = 1,\]

thus resulting in (1).

The remaining two proofs are for the infinite sum

\[1+ \lambda + \lambda ^2 + \ldots = \frac{1}{1- \lambda }\tag2\]

and positive \(\lambda<1\). 

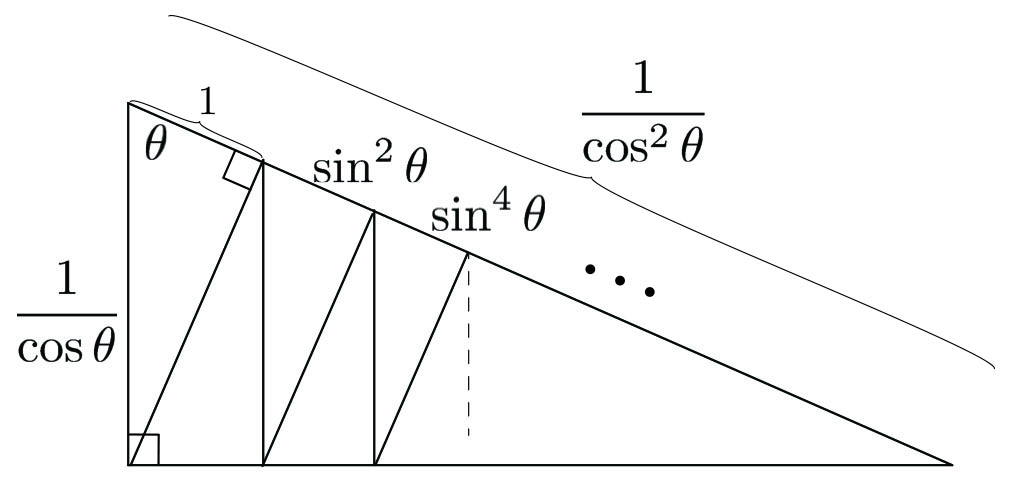
A Pythagorean Proof

The construction of Figure 2 yields a partition of the hypotenuse into an infinite union of segments of lengths \(1, \sin ^2 \theta, \sin ^4 \theta, \ldots\) On the other hand, the hypotenuse has length \((1/ \cos \theta )/ \cos \theta = \cos ^{-2} \theta\), so that

\[1+ \sin ^2 \theta +   \sin ^4 \theta + \ldots = \frac{1}{\cos ^2 \theta }.\tag3\]

This implies (2) by choosing \(\theta\) so that \(\lambda = \sin^2  \theta\), and by application of the Pythagorean theorem. As a curiosity, reversing the argument—i.e., taking (2) for granted—gives an admittedly strange proof of the Pythagorean theorem.

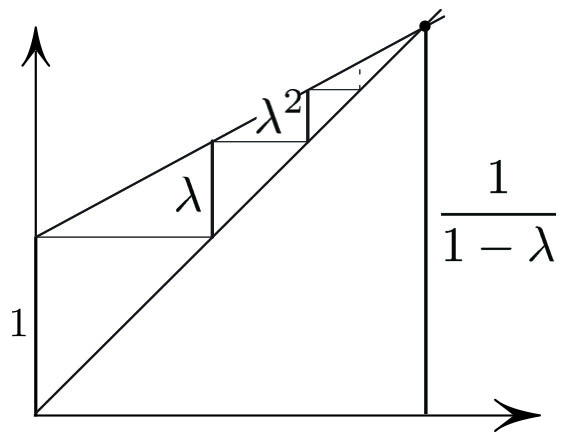
A Staircase Proof

The two lines \(y=1+ \lambda x\) and \(y=x\), which appear in Figure 1, intersect at height \(y= \frac{1}{1- \lambda }\). But this height is also the sum of rises that form a geometric sequence \(1, \lambda, \lambda ^2, \ldots\), again yielding (2).

The figures in this article were provided by the author.