Group Science: The Open Source Study of Higher-order Networks With XGI

The concept of group effects is not always intuitive. In the natural sciences, multibody interactions often involve a sum of pairwise interactions, but the natural laws that govern these interactions remain unchanged. When calculating gravitational fields, for example, Leonhard Euler’s three-body problem can yield dramatically richer behavior than the two-body problem, but the underlying physical laws are the same. However, some interactions do change in groups; opinion dynamics may work differently as social networks expand, predation preference in ecosystems shifts with community composition, and many chemical reactions require multiple reactants. It is also combinatorially challenging to model groups, as a system of 1,000 parts can contain up to \(\binom{1,000}{2}=\mathcal{O}(10^5)\) pair interactions but as many as \(2^{1,000}=\mathcal{O}(10^{301})\) groups! Researchers need new software to efficiently store group interactions, analyze their structures, simulate their dynamics, and ultimately examine their impacts on nature and society.

Social scientists have long debated the reality of groups distinctly from their individual members, as well as groups’ prospective impacts on individual behavior. Groups can develop specific norms, cultures, and sometimes seemingly minds of their own, which means that new phenomena and mechanisms can emerge at the group level. Experts have studied group ontology in sociology [10], philosophy [8], and other disciplines, but they continue to deliberate about groups’ irreducibility when compared to their members [5, 9]. These ongoing queries resonate with the philosophy of complex systems and network science, whose researchers typically embrace the fact that “the whole is more than the sum of its parts” [1]. As a result, a community has emerged in recent years that focuses on higher-order networks, contributing mathematical modeling tools, software, and large-scale datasets to solve computational challenges and improve our collective understanding of the differences between multibody interactions and mere sums of pairwise interactions.

Mathematically, higher-order networks often take the form of hypergraphs (i.e., a set of nodes and a set of arbitrarily-sized interactions, or hyperedges) or simplicial complexes (i.e., hypergraphs with an added constraint of downward closure so that every sub-interaction exists within a given hyperedge) [7]. Unlike pairwise networks, where groups are simply implied as dense subgraphs within a network’s structure, higher-order networks explicitly model groups and thus facilitate the modeling of group-level dynamics.

Barriers to Working With Higher-order Networks

However, higher-order networks pose several challenges. First, they can be extremely computationally expensive; exhaustive computation quickly becomes infeasible at the scale of practical applications. For instance, coauthorship networks can easily include millions of authors and publications. In contrast, empirical higher-order networks are often quite sparse, and large groups are much less common than smaller ones. Network analysis algorithms leverage these properties to sidestep such combinatorial limitations and enable the study of empirical higher-order systems at scale. But higher-order datasets themselves pose difficulties as well, as a lack of standardized formats promotes ad hoc methods for data processing.

Overcoming these challenges requires efficient, user-friendly software that is integrated with large-scale datasets. Just as NetworkX, igraph, and graph-tool have become the lingua franca of network science software, newer software packages have materialized to handle the demands of higher-order network science: an analogue of pairwise network science in the age of big data. These packages provide a common language through which higher-order network scientists across diverse disciplines can collaborate via network data structures, efficient algorithms, and integration with large-scale network datasets.

The XGI Research Ecosystem

The CompleX Group Interactions (XGI) software package is an open source Python library for the analysis of higher-order networks [6]. XGI addresses the aforementioned challenges by offering a comprehensive ecosystem for higher-order network science research through a suite of analytical tools, seamless integration with a corpus of large-scale datasets, and extensive tutorials and documentation. The library can represent undirected and directed hypergraphs and simplicial complexes; read and write networks that are stored in common file formats; convert between different data structures; clean up common data artifacts; generate synthetic networks from random and classic models; analyze network properties such as clustering, assortativity, path lengths, node and group centrality, and connectedness; simulate dynamics; and visualize these networks.

XGI represents higher-order networks as a data structure, storing all node-group relationships for efficient computation. However, this depiction is not always suitable for all applications; for example, spectral measures of hypergraph structure rely on matrix representations. To account for this limitation, XGI can convert to and from more than 10 different higher-order data structures, including representative matrices, lists of groups, and node-group relationships. In particular, the field has especially advanced in the efficient measurement of higher-order statistics and generation of synthetic hypergraphs. In several cases, XGI’s state-of-the-art algorithms have improved performance by several orders of magnitude when compared to exhaustive computation.

XGI is integrated with the XGI-DATA repository: an open data repository on Zenodo that hosts 44 datasets of diverse domains, systems, and sizes. Each dataset is accompanied by computed statistics and information, such as how and when the set was collected, who created it, what the nodes and edges represent, and how to cite it. A single command loads the datasets via an HTTP request, streamlining scientific workflows. In parallel, the Hypergraph Interchange Format exists as a data sharing standard [3] to facilitate the sharing of higher-order network data between different scientific software packages and research teams.

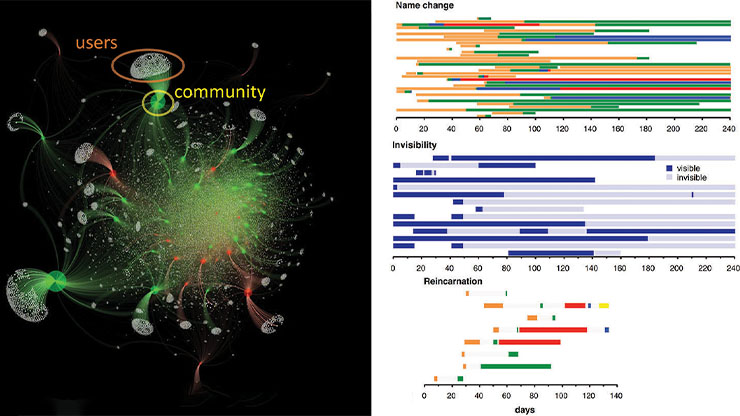
As an example of XGI’s potential, Figure 1 depicts the arxiv-kaggle dataset from XGI-DATA. This dataset comprises 1.8 million nodes (authors) and 2.8 million hyperedges (publications) that are loaded into XGI with the load_xgi_data method. XGI’s cleanup method enables data cleaning, which removes single-author papers and papers that fall outside of the largest connected component — a technique that is useful to many data science pipelines. The H.edges.filterby() method then filters the dataset with a custom filtering function, which extracts papers that have two or three authors and “hypergraph,” “higher-order,” or “simplicial” in the title — ultimately yielding a hypergraph with 593 nodes and 518 hyperedges. The filterby method is an example of XGI’s statistics interface for node and edge properties, allowing users to easily convert between data formats, compute statistics on these properties, and even define one’s own statistics. We can visualize the dataset with xgi.draw(H), where the node colors signify the average occurrence of higher-order keywords in the papers with which they are affiliated.

We can analyze this hypergraph in a variety of ways. First, we can leverage different data representations to unlock various measures from linear algebra or pairwise network analysis. Second, we can simulate multiple dynamics—such as the Kuramoto model or hypergraph susceptible-infected-recovered model—on the hypergraph to analyze the resulting behavior. We are also able to generate synthetic higher-order networks with tunable structure, which may serve as null models or the theoretical foundation for analytical measures of structure or dynamics. And finally, we can measure the structure of a higher-order dataset to quantify degree assortativity, simpliciality, clustering coefficients, and so forth. A great place to start is the XGI project website, which contains a comprehensive collection of documentation and tutorials.

Looking to the Future

Toy models have already demonstrated the importance of group effects. Simple mathematical models of contagion that are mediated through group dynamics naturally exhibit phenomena that exist in the real world—e.g., polarization, collective action, and tipping points [2, 4]—and are often generated by a critical mass of influential groups, rather than individual agents.

Researchers are now advancing the frontiers of group science on two separate fronts. First, theoretical models require validation with more observational data, necessitating new experiments and model systems. And second, certain hypothesized dimensions of group dynamics, such as group states and the alignment of rationality between groups and their members, are still somewhat unexplored [9]. The way in which groups shape our world—by mediating the flow of information, influencing the formation of ideologies, driving the spread of infectious disease, etc.—is an exciting area of study. Higher-order networks will always be more computationally expensive than their pairwise alternatives, but open source software packages that leverage efficient algorithms, large-scale datasets, and compelling visualizations are unlocking this exciting field for practitioners across a diverse range of disciplines.

References
[1] Anderson, P.W. (1972). More is different. Science, 177(4047), 393-396.
[2] Burgio, G., St-Onge, G., & Hébert-Dufresne, L. (2025). Characteristic scales and adaptation in higher-order contagions. Nat. Commun., 16, 4589.
[3] Coll, M., Joslyn, C.A., Landry, N.W., Lotito, Q.F., Myers, A., Pickard, J., … Szufel, P. (2025). HIF: The hypergraph interchange format for higher-order networks. Preprint, arXiv:2507.11520.
[4] Iacopini, I., Petri, G., Barrat, A., & Latora, V. (2019). Simplicial models of social contagion. Nat. Commun., 10(1), 2485.
[5] Lackey, J. (2021). The epistemology of groups. Oxford, UK: Oxford University Press.
[6] Landry, N.W., Lucas, M., Iacopini, I., Petri, G., Schwarze, A., Patania, A., & Torres, L. (2023). XGI: A Python package for higher-order interaction networks. J. Open Source Softw., 8(85), 5162.
[7] Landry, N.W., Young, J.-G., & Eikmeier, N. (2024). The simpliciality of higher-order networks. EPJ Data Sci., 13(1), 17. 
[8] Pettit, P. (2001). Collective intentions. In N. Naffine, R. Owens, & J. Williams (Eds.), Intention in law and philosophy. London, UK: Routledge.
[9] St-Onge, J., Harp, R., Burgio, G., Waring, T.M., Lovato, J., & Hébert-Dufresne, L. (2025). Defining and classifying models of groups: The social ontology of higher-order networks. Preprint, arXiv:2507.02758.
[10] Warriner, C.K. (1956). Groups are real: A reaffirmation. Am. Sociol. Rev., 21(5), 549-554.