Hierarchical Digital Twins for Simulation, Optimization, and Control

Volker Mehrmann of Technische Universität Berlin routinely tackles difficult problems in systems modeling and control via port-Hamiltonian formulations. These are like special zoom lenses on a digital camera; without shifting position, a photographer can zoom in to capture the finest details or zoom out to view the entire scene, all while achieving the desired fidelity in each part of the image.

During the 2021 SIAM Conference on Computational Science and Engineering (CSE21) earlier this year, Mehrmann—who received SIAM’s 2018 W.T. and Idalia Reid Prize—described how this metaphoric lens can capture digital twins of complex, spatially distributed systems like natural gas networks or district heating plants. Digital twins are computational clones of physical systems that enable “simulation, optimization, and control in real time,” he said.¹

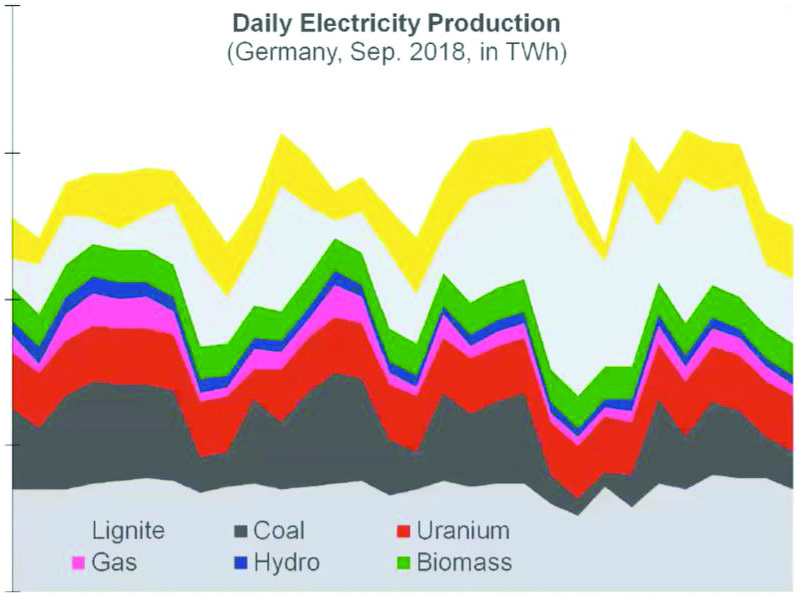
Mehrmann was motivated by the German government’s decisions to phase out both nuclear and coal-fired power generation. Daily demand for gas-fired electric power—one of the remaining alternative sources—is already highly variable and tightly coupled to the demand for other sources. The chart in Figure 1 illustrates both complications by depicting Germany’s electric power production by source over a single month.

In Mehrmann’s paradigm, digital twins are composed of a hierarchy of networked models of various physical systems: mathematical statements of fundamental physical laws with their inputs, states, outputs, and parameters. These systems are coupled with data-driven models that relate measurements of parameters and sensor data to enable monitoring and state estimation.

For example, one might construct a coarse digital twin of a large natural gas network by applying the one-dimensional Euler equations to the flow in each of the pipes in a large-scale, country-level diagram of the network. Zooming in closer summons the hierarchy of models. What appears to be a network node from a distance becomes a local network of its own when magnified — perhaps a multi-stage compressor station or an interconnected array of switching valves. However, the pieces at each level are essentially pipes, pumps, and finer-grained networks. The hierarchy is thus composed of networks that are nested within networks; each stage of refinement introduces models with higher levels of accuracy and fidelity.

Modeling finer details can of course increase a digital twin’s accuracy, but at the cost of slowing the computations. Less precise modeling at a certain level—a stationary approximation of some component, for instance—might compensate for the added CPU time without an unacceptable loss of accuracy. Alternatively, one might replace the burden of solving a complex partial differential equation (PDE) with a reduced-order input-output model, such as a simple expression that relates head to flow rate in a compressor station. The challenge is hierarchically zooming in or out to economically obtain the accuracy that is necessary for the purposes at hand without painstakingly rebuilding the entire model.

The ambitions of Mehrmann’s digital twin “modeling wish list” encompass physics, engineering, numerics, and analysis. He aims to develop coupled models that function across different scales and physical domains while remaining close to the real physics for open and closed systems. The formulation should discretize easily in space and time to support simulation, control, and optimization, and the models’ analytic properties should include all of the essential credentials of existence, stability, etc. Finally, Mehrmann wants to reach these goals within a strong systems-theoretic framework.

This mathematical framework is built with the widely applicable formulation that is known as dissipative port-Hamiltonian (pH) systems. The word “port” evokes the connections through which model components exchange information with one another; “Hamiltonian” evokes energy, the lingua franca of these exchanges. Intuitively (albeit crudely), the resistors, inductors, and capacitors that comprise an RLC circuit are examples of pH elements. Energy in each element is a time integral of power, which is itself a product of the current through the element and voltage drop across it (flow multiplied by effort). Because of the resistor, the energy in each element obeys a dissipation inequality rather than an equality.

A power-conserving ensemble of these pH circuit elements, such as an ordinary RLC circuit, forms another pH system. When augmented by the constraints of Kirchhoff’s Current and Voltage Laws—themselves a set of differential-algebraic equations (DAEs)—the simplest variety of pH DAE system emerges. Formalizing the underlying dual-space geometry, extending to infinite dimensions, and incorporating time-dependent PDEs then lay the foundation for the mathematical half of Mehrmann’s paradigm shift: a hierarchical structure of pH DAE models that preserves their properties, including the dissipation inequality, through model reduction.

The computational requirements are similar in spirit and involve the preservation of key pH DAE properties during spatial and temporal discretization. Galerkin projection can discretize spatial variables as needed, and time discretization must preserve the pH conservation and dissipation requirements up to the discretization error.

Computational experiments have demonstrated some of the successes of pH DAE systems. For example, Mehrmann and his collaborators studied a four-level gas transport model hierarchy to adaptively manage the compromises between error tolerance and computational speed when constructing a digital twin. After determining sensitivities within the hierarchy as well as error estimates for the space and time discretizations, they fit a cost function that relates space and time discretization errors to CPU time. The “truth” was an expensive isothermal Euler equation model; the adaptive test offered three successive hierarchical stages of simplification. The adaptively constructed model reduced the four-hour runtime that was required by the original formulation by 80 percent [1, 5].

A similar effort with more complex gas networks demonstrated that an adaptive strategy can also construct an efficient digital twin to optimize the cost of compressor operation [4]. Another study displayed an effective tool for optimizing household power consumption in a district heating network whose capacity for generating power via waste incineration was limited [3].

How did Mehrmann’s digital twin modeling wish list fare? He declared that “pH systems are great, and almost all wishes are fulfilled.” Of course, much work remains. Mehrmann’s to-do list includes the incorporation of real-time control and optimization, different physical domains, stochastic elements, stability analysis, error estimation, and new software, among other components.

¹ For another perspective on digital twins, see the SIAM News article [2] from September 2021 in which Karen Willcox and Michael Kapteyn recap Willcox’s CSE21 talk. 

References

[1] Domschke, P., Dua, A., Stolwijk, J.J., Land, J., & Mehrmann, V. (2018). Adaptive refinement strategies for the simulation of gas flow in networks using a model hierarchy. Elect. Trans. Numer. Analys., 48, 97-113.
[2] Kapteyn, M.G., & Willcox, K.E. (2021, September 1). Digital twins: Where data, mathematics, models, and decisions collide. SIAM News, 54(7), p. 1.
[3] Krug, R., Mehrmann, V., & Schmidt, M. (2020). Nonlinear optimization of district heating networks. Opt. Engin., 22, 783-819.
[4] Mehrmann, V., Schmidt, M., & Stolwijk, J.J. (2018). Model and discretization error adaptivity within stationary gas transport optimization. Vietnam J. Math., 46, 779-801.
[5] Stolwijk, J.J., & Mehrmann, V. (2018). Error analysis and model adaptivity for flows in gas networks. Analele Stiintifice ale Universitatii Ovidius Constanta, Seria Matematica, 26(2), 231-266.