High-fidelity Digital Twins

A 2020 position paper by the American Institute of Aeronautics and Astronautics and the Aerospace Industries Association defines a digital twin (DT) as “a set of virtual information constructs that mimics the structure, context, and behavior of an individual/unique physical asset or a group of physical assets, is dynamically updated with data from its physical twin throughout its life cycle, and informs decisions that realize value” [3]. This definition implies several key ingredients:

• The physical asset in the form of a product, process, or patient
• A set of sensors or measuring devices that monitor the physical asset
• A digital model of the asset
• A feedback loop that updates the model based on sensor data.

Traditional models start with a generic physical law (e.g., equations) and are often a simplification of reality, but DTs start with a specific ecosystem, object, or person in reality and require multiscale, multiphysics modeling and coupling. Because these processes begin at opposite ends of the simulation and modeling pipeline, they require different reliability criteria and uncertainty assessments. Additionally, DTs help humans make decisions for the physical system—which uses sensors to feed data back into the DT—and operate for the system’s entire lifetime. 

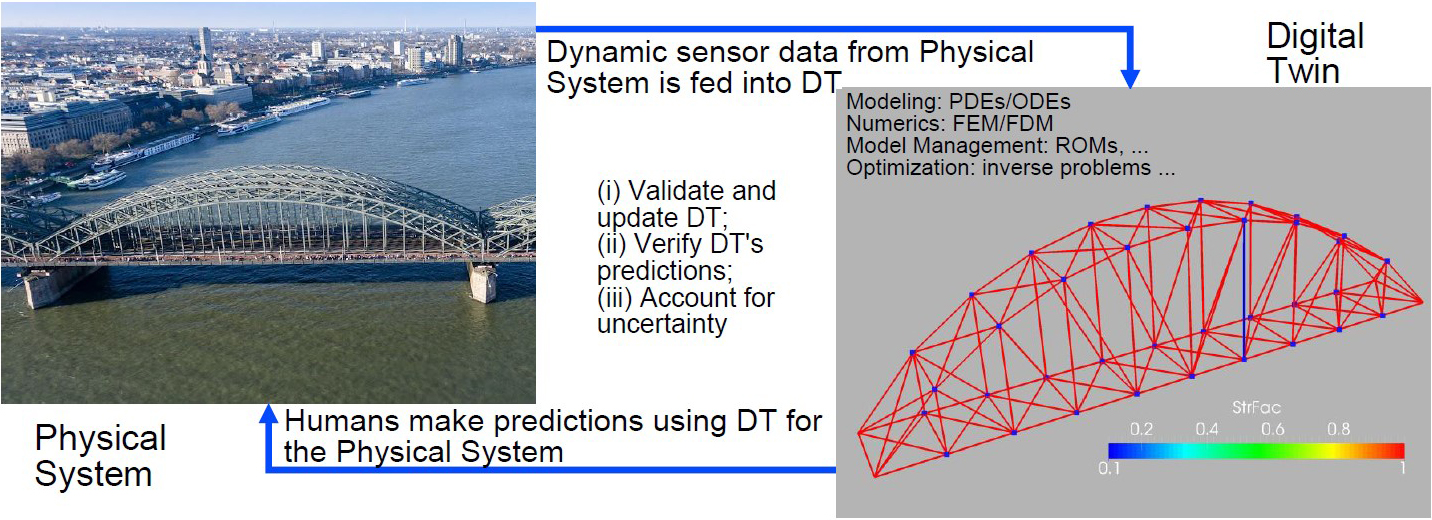
DTs offer foundational mathematical challenges and opportunities with the potential for significant impact, but how did they come about? They emerged as the result of three major trends: (i) The pervasive use of computer-aided design (CAD) systems, (ii) the widespread availability of computational tools to “pre-compute, then build” and “pre-compute, then operate,” and (iii) the emergence of precise, rugged, connected, and cheap cameras and sensors to monitor structures. See Figure 1 for a comparison between an actual bridge and its unique DT.

Types and Hierarchies of Digital Twins

DT can mean different things in different realms, even within specialized fields like civil engineering. The data stored within a DT can also encompass vastly different information. For instance, some civil engineers consider a building information modeling enumeration of parts (e.g., the number of buildings in a neighborhood) to be a DT. The appropriate numbers in this framework are updated as new buildings or roads are added. Users may enrich this data by accounting for the parts (number, type, dimensions, or manufacturer of walls, doors, flooring, piping, lighting, etc.); including the CAD data for visualization or product life cycle management enriches the data further, and utilizing detailed or approximate computational models and sensors that monitor aspects of the built environment provides an additional level of enrichment. 

High-fidelity DTs are those whose underlying models exhibit high-fidelity physics, either in the form of a spatial and/or temporal discretization of the partial differential equations (PDEs) that described the physics (structure, fluid, heat, electromagnetics, mass, etc.), or a reduced order model of the same. The degree of useful fidelity depends on the quality and quantity of the available sensors, as well as the decision space of the engineers who are monitoring the asset (e.g., repairing or demolishing a bridge).

Recent Workshops, Recommendations, and Mathematical Challenges

Given the recent interest in DTs, a number of organizations have commissioned reports on the subject. Some of the most prominent are a National Academies report titled “Foundational Research Gaps and Future Directions for Digital Twins” [7], a report on the 2023 “Crosscutting Research Needs for Digital Twins” workshop at the Santa Fe Institute, and a report on the National Science Foundation’s workshop on “Mathematical Opportunities in Digital Twins (MATH-DT)” at George Mason University [4]. These publications identified several challenges and opportunities that pertain to DTs.

Better Preprocessors: DTs require constant updating of physical parameters, boundary conditions, loads, and sometimes even geometry for the physical models that describe them. This requisite implies a need to revise or “curate” the DT models for different types of dynamics. Once a change occurs (e.g., a part is adjusted in a turbine), the complete set of models must be rerun to ensure that the product/process is safe and the DT is up to date. This procedure is extremely expensive if not automated, thus hampering the widespread adoption of DTs. Given that most current products/processes are computed first and then built/executed, we must develop CAD tools and métier-specific preprocessors that allow the DT to update automatically throughout the life cycle of the product/process in question. We need DTs that can incorporate data, as well as software and algorithms that are tuned to DT frameworks.

Gaps in Forward Problems: The basic physics of many problems in engineering, biology, medicine, and materials science are still unknown, so we may not know which PDEs or ordinary differential equations (ODEs) are relevant. And even if we are familiar with the basic physics, the uncertainty in the physical parameters could be very large (due to factors such as material parameter variations or the inability to obtain good measurements). While DT research does not necessarily fall squarely in the realm of applied mathematics, it is nonetheless important to obtain a rigorous understanding of the basic properties of the PDEs and ODEs that describe emerging physics concepts, including uniqueness, stability, convergence, asymptotic behaviors, and reduced order modeling.

Coupled Models, Physics, and Scales: For some classes of problems, even simple descriptions of physical reality may require a coupling of models (fluid, structure, heat, etc.) across many length and time scales. Other problems may require coupling models of different dimensional abstractions (e.g., beams, shells, and solid elements in a finite element model of a bridge). Mathematics plays a key role in assuring that this coupling of models, physics, and scales leads to unique, stable, and convergent answers for the creation of valid DTs.

Optimization and Inverse Problems: We must solve inverse problems to infer properties of the DT’s real-life object/process, such as when a DT helps a human make decisions about the physical model. The most expedient way to discern the unknowns is through the use of optimization via the so-called method of adjoints. The theory of adjoint solvers is well developed for classic PDEs, including elasticity or incompressible flow; for more complex physics or models, however, the adjoints may be nonexistent or difficult to obtain. The situation is quite challenging even in classical settings like bilevel optimization, optimal experimental design, or situations with discrete design variables. These problems are nonconvex, nonsmooth, and potentially multi-objective. As such, there is a real need for further in-depth mathematical analysis and algorithm development for these tough problems and adjoints.

Uncertainty Quantification and Optimization Under Uncertainty: Every step of the decision-making process—from modeling and forward problems to optimization and engineering design—should account for uncertainty and measure the risk of extreme-case scenarios. The resulting forward and optimization problems with uncertainty are nonconvex, nonsmooth, high dimensional, and unsolvable with traditional approaches. The underlying probability distribution may have ambiguity [5].

Workforce Development: DTs are intrinsically the result of multidisciplinary efforts. They involve model preparation, model execution, sensor input, system output analysis, inference of the system’s state from measurements, and model update/upkeep. To effectively deploy DTs and experience their potential societal benefits (e.g., increased safety, greater comfort, longer life cycles, reduced environmental footprint), current and future developers and users will require proper training. Specifically, the workforce will need a combination of classic and modern numerical methods (PDEs, optimization, numerical linear algebra, randomized methods, reduced order modeling, etc.), statistics and uncertainty quantification (sensors, forces, actuators, etc.), computer science techniques (basic programming skills, large data sets, etc.), and engineering.

An Example of High-fidelity Digital Twins

Let us consider the identification of weaknesses in a footbridge. Mathematically, the DT problem in Figure 1 is an optimization problem with elasticity equations as PDE constraints. Let the physical domain be given by \(\Omega\) and let the boundary \(\partial\Omega\) be partitioned into the Dirichlet \((\Gamma_D)\) and Neumann \((\Gamma_N)\) parts. The optimization problem that identifies weakness in the structure—i.e., coefficient function \(z\)—is given by

\[\min\limits_{(\pmb{u},z)\in U\times Z_{\rm{ad}}}  \; J(\pmb{u},z) \quad \textrm {subject  to} \quad -\textrm{div}(\pmb{\sigma}(\pmb{u};z))=\pmb{f}, \tag1\]

with \(\pmb{u}=0\) on \(\Gamma_D\) and \(\pmb{\sigma}(\pmb{u};z)\nu=0\) on \(\Gamma_N\). Here, \(\pmb{\sigma}\) is the stress tensor, \(\pmb{f}\) is the given load, \(Z_\textrm{ad}:=\{z\in L^2(\Omega) \, : \, 0 < z_a \le z\le z_b  \: \textrm{a.e.} \: x \in \Omega \}\) is a closed convex set with \(z_a,z_b \in L^\infty (\Omega)\), and \(J\) indicates the misfit between the displacement \(\pmb{u}\) or strain tensor and their respective measurements (displacement or strain).

Figure 2a illustrates the results for the target displacement and sensor locations, and Figure 2b shows the target strength factor \((z)\). Figures 2c and 2d present a solution to the optimization problem in \((1)\) under various loading conditions with respective displacement and strength factors.

The load \(\pmb{f}\) is uncertain in Figure 3, which compares the results from standard expectation versus a risk measure — i.e., conditional value at risk with a confidence level of \(\beta\) [1].

Outlook

DTs are here to stay and have several potential future directions [4, 7]. In the mindset of academia, industry, software companies, funding agencies, and potential users, DTs require foundational mathematical advances that differ from traditional fields. Making DTs a reality will hence require considerable advances in areas such as large-scale nonconvex optimization/inverse problems, data assimilation, sensor placement, multiscale and multiphysics modeling, uncertainty quantification, model order reduction, scientific machine learning, quality assessment, process control, rapid statistical inference, online change detection for actionable insights, and software development. Some methods may only work well in certain fields, while others might be more general.

We must also develop benchmark test problems and data sets for different applications, including bridges (civil engineering), vibrating beams (mechanical engineering), and sepsis (medicine) [4, 6]. The creation of mathematical and statistical principles for DT model updates and maintenance is equally critical.

Acknowledgments: This work is partially supported by U.S. National Science Foundation grants DMS-2110263 and DMS-2330895, the Air Force Office of Scientific Research under Award No. FA9550-22-1-0248, and the Office of Naval Research under Award No. N00014-24-1-2147.

References

[1] Airaudo, F., Antil, H., Löhner, R., & Rakhimov, U. (2024). On the use of risk measures in digital twins to identify weaknesses in structures. In AIAA SCITECH 2024 forum (pp. 2622). Orlando, FL: Aerospace Research Central. 
[2] Airaudo, F.N., Löhner, R., Wüchner, R., & Antil, H. (2023). Adjoint-based determination of weaknesses in structures. Comput. Methods Appl. Mech. Eng., 417(A), 116471.
[3] American Institute of Aeronautics and Astronautics Digital Engineering Integration Committee. (2020). Digital twin: Definition & value (AIAA and AIA position paper). Reston, VA: American Institute of Aeronautics and Astronautics. Retrieved from https://www.aiaa.org/docs/default-source/uploadedfiles/issues-and-advocacy/policy-papers/digital-twin-institute-position-paper-(december-2020).pdf.
[4] Antil, H. (2024). Mathematical opportunities in digital twins (MATH-DT). Preprint, arXiv:2402.10326.
[5] Antil, H., Carney, S.P., Díaz, H., & Royset, J.O. (2024). Rockafellian relaxation for PDE constrained optimization with distributional ambiguity. Preprint, arXiv:2405.00176.
[6] Laubenbacher, R., Mehrad, B., Shmulevich, I., & Trayanova, N. (2024). Digital twins in medicine. Nat. Comput. Sci., 4(3), 184-191.
[7] National Academies of Sciences, Engineering, and Medicine. (2024). Foundational research gaps and future directions for digital twins. Washington, D.C.: National Academies Press. Retrieved from https://nap.nationalacademies.org/catalog/26894/foundational-research-gaps-and-future-directions-for-digital-twins.