High-throughput Screening Systems for Drug Discovery and Virus Detection: A Parametric Graph Approach

Advances in human genomics, combined with the ongoing need to discover viruses and new drugs, require the ability to test an ever-larger number of biochemical compounds and process thousands of samples in a very short period of time. Pharmaceutical and biomedical researchers often use high-throughput screening (HTS) systems—a type of intelligent robotic cell—to analyze new chemicals, discover new drugs, and detect new viruses. A standard HTS system tests between 10,000 to 100,000 compounds per day, while an ultra-HTS system screens more than 100,000 compounds per day. These substances are fed into the robotic cell on microplates that the robot sequentially transports between workstations in accordance with the screening procedure — and in such a way that each plate can re-enter each workstation if necessary. The HTS cell includes a fixed set of workstations that perform preparation, deposition, liquid dispensing, reading and analysis, and incubation operations.

The overall goal of our technique is to find a cyclic schedule of robotic moves that minimizes cycle time and therefore maximizes cell performance. In terms of scheduling theory, the scheduling problem in question involves a single-robot, multiple-machine cyclic flowshop problem with blocking and re-entrance. This type of schedule optimization can minimize the total screening time, thus reducing cost and enabling quick discovery of new drugs or disease diagnoses.

However, the problem at hand has a complex combinatorial structure (in fact, it is NP-hard) and is difficult to solve. Research in recent decades has revealed many mathematical methods for finding optimal HTS schedules, such as greedy empirical heuristics, max-plus algebra, and genetic algorithms. Unfortunately, none of these methods—some of which have prohibitively high exponential computational complexity—can guarantee an optimal solution for arbitrary input data in a short computation time. Advanced mathematical techniques like mixed-integer programming (MIP), Petri nets, and extremal path routing in graphs can help solve the problem and outperform known empiric solutions. However, MIP and Petri net techniques only work effectively in practice for small and medium-sized problems, while the required computation time for large-scale models is—in the worst case—exponentially dependent on the number of integer variables. This limitation raises the following question: Is there a polynomial-time algorithm that solves the scheduling problem under a study of reasonable size? 

To address this query, we developed an efficient parametric graph-based critical path method (PGM) and used theoretical analyses of the HTS process for enzymatic assay to demonstrate its validity and practical applicability. Although the scheduling problem under consideration is complex and NP-hard, we can use our algorithm to solve this problem efficiently in practice if the number of operations is bounded by a constant (this is a special case that is commonly encountered in practice). The proposed PGM algorithm works in conjunction with an efficient procedure for eliminating infeasible schedules, and our algorithmic result generated by the combined PGM algorithm—which cannot be achieved with existing methods—complements previous studies [1, 2, 4, 5].

Problem Description

Enzymatic assays are a typical application of HTS systems. In this setting, an HTS system generally includes the following basic workstations (see Figure 1):

1. Cytomat 2C, a microplate hotel that prepares microplates for screening
2. Multidrop 384, which dispenses liquid substances into microplate wells
3. An envision device that identifies and analyzes changes in the biochemical substances
4. Teleshake, a device that maintains a required environment and allows the biochemical substances in the microplate wells to incubate
5. A storage center that holds the microplates for screening.

As the microplates periodically enter the robotic cell, a SCARA robot transports them between workstations and an auxiliary device automatically moves them from the storage center to the Cytomat 2C so that the system can continuously operate without interruption. During our screening process, each microplate passes the workstations in the same technological sequence: Cytomat 2C \(\rightarrow\) Multidrop 384 \(\rightarrow\) Envision \(\rightarrow\) Teleshake \(\rightarrow\) Envision \(\rightarrow\) Cytomat 2C. This predetermined technological sequence of workstations is as follows: \(M_0, M_1, M_2, M_3, M_2, M_0\), where \(M_i\), \(i = 0,1,2,3,2,0\) designate the respective workstations (see the corresponding cyclogram in Figure 2).

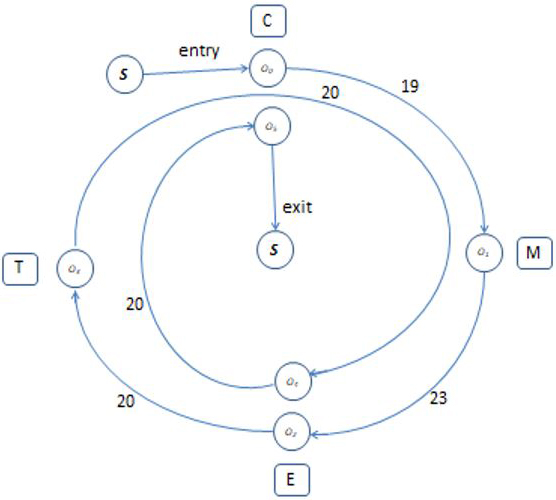
Letters inside the nodes \((O_0, O_1, ..., O_5)\) indicate operations that are performed on workstations, and numbers inside the nodes indicate the required time for the corresponding activity. The arcs between nodes and the related arc weights respectively denote the robot’s delivery operations and their durations. Each operation \(O_k\), \(k= 0,1,..., 5\) is characterized by the following parameters:

• \(p_k\): the processing time of operation \(O_k\), \(k=0,1,...,5\)
• \(d_k\): the time required for a robot to deliver a microplate from a workstation that is performing operation \(O_k\) to the next workstation in technological sequence \(S\), \(k=0,1,...,5\)
• \(l_k\): lower bound for processing time of operation \(O_k\): \(p_k\ge l_k\), \(k=0,...,5\). 

A cyclic schedule is a schedule that repeats itself at fixed intervals of time \(T\) known as cycle times. If \(k\) microplates enter and leave the robotic cell during a cycle, this schedule is called a \(k\)-degree cyclic schedule (or \(k\)-cyclic schedule). A stable schedule is one whose average optimal cycle time \({T^*}_\textrm{aver}\) is insensitive to unforeseen disturbances in certain limits — i.e., a given control policy can easily control and correct it.

We introduce a fast scheduling algorithm that utilizes two conjugate sub-algorithms to solve the problem. The first sub-algorithm is the parametric version of the PGM — which treats the case where (i) all of the processing times lie within given time intervals (called time windows) and (ii) the number of processing operations is bounded by a constant, as is the case of the enzymatic assay in practice. This sub-algorithm can handle all of the robot’s feasible routes and identify the minimum cyclic time using an existing advanced parametric graph algorithm [1], which we modified for this work. 

Among all available routes, the first sub-algorithm selects the one with the lowest cycle time. This sub-algorithm outputs an optimal 1-cyclic robot route. Next, we introduce the second sub-algorithm, whose input is the optimal processing times \(p_k\) of all operations as provided by the first sub-algorithm. The second sub-algorithm finds a set of different optimal 2-cyclic robot schedules. Using a modified version of the Method of Excluded Intervals (MEI) [2], we eliminate infeasible schedules and obtain an optimal stable 2-cyclic schedule in strongly polynomial time. Figure 3 shows a fragment of a resulting parametric graph, the arc length of which may depend on the parameter: the cycle time \(T\). The length of the critical path equals the minimum cycle time value.

Main Theoretical and Computational Results

The solution of the best instance of the considered problem is the following: \(T=200.5\), \(t_1=39\), \(t_2=116\), \(t_3=145.5\), \(t_4=19\), \(t_5=73\), \(t_6=168.5\). The following statement defines the robot route we are looking for.

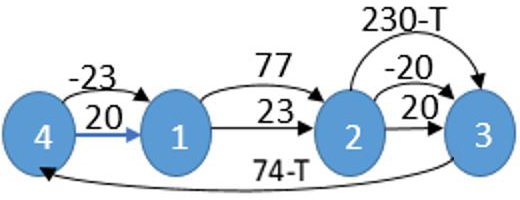
Claim 1. Given real numbers \(T\) and \(T_1\), arrange the numbers \(t_i\) and \(t^\prime_i\) in increasing order: \({t^*}_{[1]}<{t^*}_{[2]}<...<{t^*}_{[10]}\), where \({t^*}_i\) denotes either \(t_i\) or \(t^\prime_i\). This order induces the sequence of operations \(R=(O_{[1]},O_{[2]},...,O_{[10]})\), which is the only possible optimal 2-cyclic robot route with period \(T\). 

Claim 2. The integrated PGM/MEI algorithm generates a package of optimal 2-cyclic schedules with cycle times of the following form \((T_1+x, T_2-x)\), where \(x\) is a parameter. Specifically for the considered enzymatic assay scheduling problem, we get \(T_1=191\), \(T_2=210\), and \(x \in [0, 9.5]\). This solution includes as particular cases the optimal solutions that resulted from existing methods [4, 5]. In the case of \(x=9.5\), we obtain the 1-cyclic schedule \(T=T_1=T_2=200.5\) [5]; if we set \(x=0\), we get a 2-cyclic schedule where \(T_1=191\) and \(T_2=210\) [4].

Claim 3. The integrated PGM/MEI generates stable optimal 2-cyclic schedules. To verify the validity of this statement, let a resulting 2-cyclic schedule with times \((T_1, T_2) = (191+x, 210-x)\) be fixed for some \(x \in (0, 9.5)\). Assume that due to a unforeseen disruption in the processing times of operations, a certain microplate (instead of the planned cycle time \(T_1\)) works longer; that is, the cycle time becomes \(T_1 + \delta\). The process controller then selects the next scheduled microplate to start \(\delta\) time units earlier, so that the next cycle time will be \(T_2 - \delta\). This control strategy ensures that the average cycle time remains the same, i.e., \(T_\text{aver}=(T_1 + \delta +T_2 -\delta)/2 = (T_1+T_2)/2\), which shows that the resulting schedule is optimal and stable.

Concluding Remarks

The worst-case complexity of the parametric graph algorithm is the same as the complexity of the corresponding pathfinding algorithm in [1], that is, \(O(m^3)\). The complexity of MEI in [2] is \(O(m^3\log m)\). Therefore, the worst-case complexity of the combined PGM algorithm is \(O(m^3\log m)\). 

Note that the proposed algorithm is fast even beyond the considered HTS system with six operations. It runs in strongly polynomial time for an arbitrary number of operations. Researchers could employ this technique to schedule more complex practical biochemical processes with a larger number of workstations and operations.

Eugene Levner delivered a contributed presentation on this research at the 2023 SIAM Conference on Control and Its Applications, which took place in Philadelphia, Pa., last year. An extended version of the paper was recently accepted for publication [3].

References

[1] Levner, E., & Kats, V. (1998). A parametric critical path problem and an application for cyclic scheduling. Discret. Appl. Math., 87(1-3), 149-158. 
[2] Levner, E, Kats, V, & Levit, V.E. (1997). An improved algorithm for cyclic flowshop scheduling in a robotic cell. Euro. J. Oper. Res., 97(3), 500-508.
[3] Levner, E., Kats, V., Yan, P., & Che, A. (2024). Fast algorithm for high-throughput screening scheduling based on the PERT/CPM project management technique. Algorithms, 17(3), 127.
[4] Oke, A., Sahin, D., Chen, X., & Shang, Y. (2022). High throughput screening for drug discovery and virus detection. Comb. Chem. High Throughput Screen., 25(9), 1518-1533.
[5] Wu, N.Q., Qiao, Y., Li, Z.W., Al-Ahmari, A.M., El-Tamimi, A.-A., & Kaid, H. (2022). A novel control-theory-based approach to scheduling of high-throughput screening system for enzymatic assay. IEEE Trans. Syst. Man Cybern. Syst., 52(12), 7667-7678.