How Do Snakes Slither? A Recipe for Reptation

While biking uphill one day, I saw a snake crossing the path ahead of me. The pavement was a bit slippery from a recent rain shower, and the snake slid rather inefficiently towards the grass on the opposite side of the path while also sliding down the slope. But once in the grass, the snake shot almost as an arrow and slithered perfectly with virtually no sideways motion (see Figure 1). Its body sliced through the grass as if constrained to a tight channel. A slow motion video of all this is available on my website. The velocity constraint imposed by the grass must have been key to the efficient locomotion; the constraint was absent on the asphalt and the snake was almost helpless. This is akin to skating on ice, where the zero sideways velocity constraint on the skate is key to propulsion.

The snake slithering in the grass converts the bending/unbending effort of the body—the only thing it can do, I think—into forward motion. How exactly does the snake do it? Which muscles must it contract, and which ones must it relax? In other words, what is the recipe for such reptation?¹ Our simplified snake has a negligibly thin body that is confined to a prescribed channel, which allows only tangential motion.

After watching the snake, I realized that the pulling force \(F\) in Figure 1b is given by

\[F=\int^L_0\tau(s)k'(s)ds,\tag1\]

where \(s\) is the arclength parameter, \(\tau\) is the bending torque (see Figure 2), \(k\) is the curvature, and \(L\) is the length of the snake. 

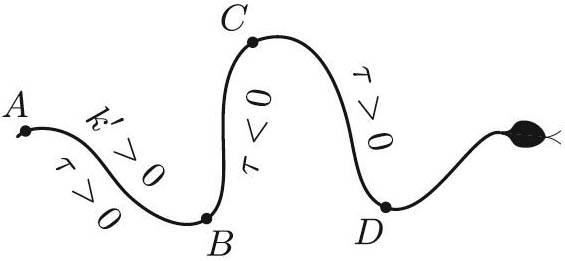
Taking \((1)\) for granted, how should the snake flex its muscles? To fix the assumptions, we take the channel in which the snake moves as given. Presumably, the very least the snake should do is make sure that \(\tau(s)k'(s)>0\) for all \(s\) in order to avoid cancellation in \((1)\) — i.e., a wasteful competition between pulling forward \((\tau k'>0)\) and backward \((\tau k'<0)\) with different parts of its body. Figure 3 illustrates this recipe for reptation: bend the body to the right (or left) if \(k\) is increasing (or decreasing).

A Dynamical Recipe for Reptation

The aforementioned recipe is good for a mathematician, but detecting \(k'(s)\) seems like a physiologically formidable task for the snake, since doing so involves the apple-versus-orange type comparison of \(k\) between two different parts of the body. How can the snake then estimate \(k'\), which it must do in some way because \((1)\) captures the physics of slithering? Here is a possible answer.

As the snake slithers along the channel, the curvature at a fixed point of the body changes from \(k(s)\) at time \(t=0\) to \(k(s+vt)\) at time \(t\) (here, \(v\) is the speed and \(s\) is measured along the channel). Therefore,

\[k'(s)=v^{-1}\partial k/ \partial t;\]

\(k'(s)\) is thus determined by \(\partial k / \partial t\), which feels like bending/unbending and hence is much easier to sense than \(k'(s)\). We can consequently restate the recipe for reptation as follows: the bending effort must coincide with the direction of bending change. That is, \(\tau\) must attempt to enhance the deformation that is imposed by travel along the channel. Or more palpably, tense the muscles that are contracting (due to bending/unbending while the snake slithers along the channel) and relax the muscles that are stretching. 

Under this recipe, the muscles do positive work — which then must go into locomotion (e.g., into overcoming friction, into acceleration, or both). 

Some Consequences of \((1)\) 

1. If the snake can exert effort \(|\tau| \le 1\) for all \(s\), then it must choose \(\tau=\textrm{sign } k'\) for the maximum pull; the resulting pull 

\[\int^L_0|k'(s)|ds\]

is the total variation of \(k\). For the snake, it thus pays to be wiggly. 

2. In contrast, adopting the shape of a circular arc is bad because \(k'(s)=0\) results in \(F=0\), regardless of the bending effort \(\tau(s)\). 

3. Figure 3 illustrates the fact that \(\tau\) must change sign at the points of maximal curvature in order to avoid having some sections of the body pull backwards. 

4. How would Euler’s elastica behave if confined to a channel? The elastica tries to straighten with moment \(\tau=-k\) (the minus sign is there because the torque resists bending if \(k>0\), thus making \(\tau<0\)). From \((1)\), we get the propulsion force 

\[\int^L_0(-k)k'(s)ds=\frac{1}{2}(k^2(0)-k^2(L)).\] 

In this case, the force depends only on the curvature at the ends.

Derivation of \((1)\) Via Potential Energy

Let us replace the live snake with an elastica that tries to bend with an intensity \(\tau(s)\) that is independent of its curvature. This is unlike Euler’s elastica, which wants to be straight with an intensity that is proportional to \(k\). In contrast with Euler’s, each element of our elastica wants to curl up with a fixed intensity \(\tau(s)\) — either left or right depending on the sign of \(\tau(s)\). The potential energy of such an element is, by definition, the work that we must do to bend the element from the straight shape to its current one (see Figure 4a). To that end, we must apply torque \(\tau\) in opposition to the one that this element applies to our hand, i.e., \(-\tau\). The potential energy of an element \(ds\) in Figure 4a is therefore

\[-\tau d\theta=-\tau kds.\]

For example, if \(\tau>0\) in Figure 4, then the element tries to curl up from the straight shape and hence does work for us (so that we do negative work). The potential energy of the “snake” in Figure 4b is therefore

\[P(\varepsilon)=-\int^L_0\tau(s)k(s+\varepsilon)ds,\]

where \(s=0\) corresponds to the tail and \(\varepsilon\) is the distance by which we advance the “snake” along the channel. Indeed, as the snake advances by \(\varepsilon\), its curvature changes to \(k(s+\varepsilon)\) while \(\tau\) remains the same by the assumption. The potential energy determines the force 

\[F(\varepsilon)=-P'(\varepsilon)=\int^L_0\tau(s)k'(s+\varepsilon)ds,\] 

which agrees with \((1)\) when \(\varepsilon=0\). 

A Geometrical Explanation of \((1)\)

The previous derivation does not explain exactly how the bending propels the snake forward. Here is an attempted explanation.

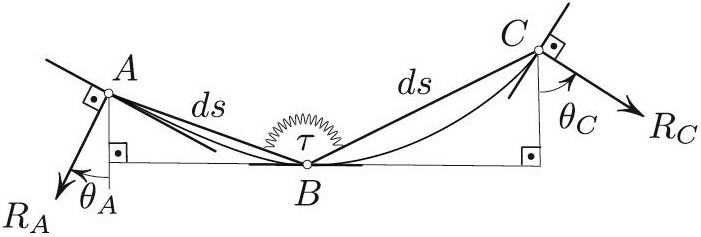
Figure 5 shows a segment of the snake that is discretized, i.e., replaced by two rods of fixed equal lengths with the ends \(A\), \(B\), and \(C\) attached to skates that can slide on the prescribed channel but cannot move transversally to it. The “muscle” at \(B\) tries to contract, i.e., \(\tau>0\). This attempted contraction results in reaction forces \(R_A\) and \(R_C\). Consider the projections of these forces onto the tangent at \(B\). If \(k'>0\), then \(\theta_C>\theta_A\), thus suggesting that \(R_C\)'s projection—which pulls \(B\) to the right—wins over its counterpart at \(A\), which pulls \(B\) to the left. This is indeed the case since \(|R_C| \approx |R_A|\) (with sufficient precision, as it turns out). 

As an alternative explanation, an infinitesimal displacement to the right of the “train” \(ABC\) in Figure 5 results in a decrease of \(\angle ABC\) because \(k(s)\) is an increasing function, and decreasing \(\angle ABC\) is exactly what the “muscle” at \(B\) attempts to do. 

¹ Some snakes, such as sidewinders, reptate by different mechanisms without obeying the velocity constraint. Here I only address one specific type of reptation. 

The figures in this article were provided by the author.