Insect Swarms, Chaos, and Phase Transitions

Midges are small flies that live on nearly every landmass across the globe. Male midges form swarms at dawn and dusk to attract females, an example of collective animal behavior that—while less flamboyant than the highly ordered, coordinated motion of flocks of birds or schools of fish—offers substantial insights into biological physics and mathematics. Swarms orient themselves in the direction of a light breeze while hovering over specific darker spots on the ground (wet areas, cow dung, manmade objects, etc.) called markers [6]. This behavior makes it possible for researchers to study swarms in the laboratory by placing markers on the floor at appropriate times. Natural swarms take different shapes depending on species, type of marker, and number of individual flies. Although they do not exhibit global order, the insects are strongly correlated, with correlation lengths that are proportional to swarm size. Understanding the formation of swarms is a significant scientific challenge, as existing models only capture partial aspects and little mathematical theory exists beyond numerical simulations. Here, we will start with observations and experiments on swarms; explain simple models, simulation results, and ensuing puzzles; and attempt to shed light on them.

By filming swarms in parks, Andrea Cavagna of Sapienza University of Rome found that certain macroscopic quantities (e.g., susceptibility and correlation length and time) obey power laws [1, 3]. In the world of physics, this observation suggests that midge swarms somewhat resemble a phase transition that is similar to the paramagnetic-ferromagnetic transition at the Curie temperature. In equilibrium phase transitions, the so-called critical exponents of these power laws are universal and have the same values for a range of phenomena and for models that belong to the same universality class [10]. With this analogy in mind, Cavagna and his collaborators defined correlation functions and measured critical exponents that can characterize the “swarm universality class.” Mathematical models with phase transitions that produce critical exponents that are compatible with measured values belong to the same universality class.

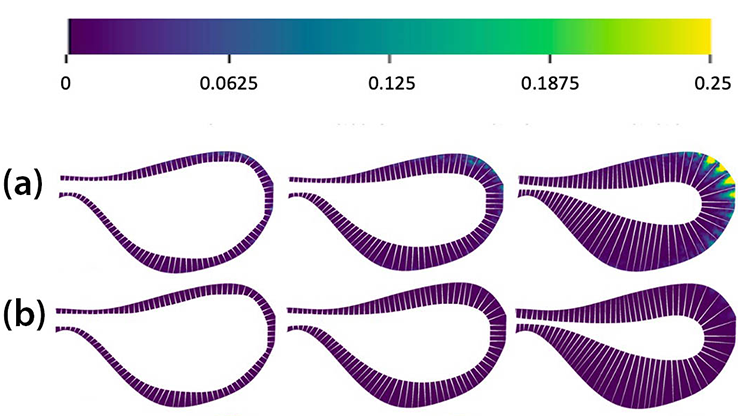
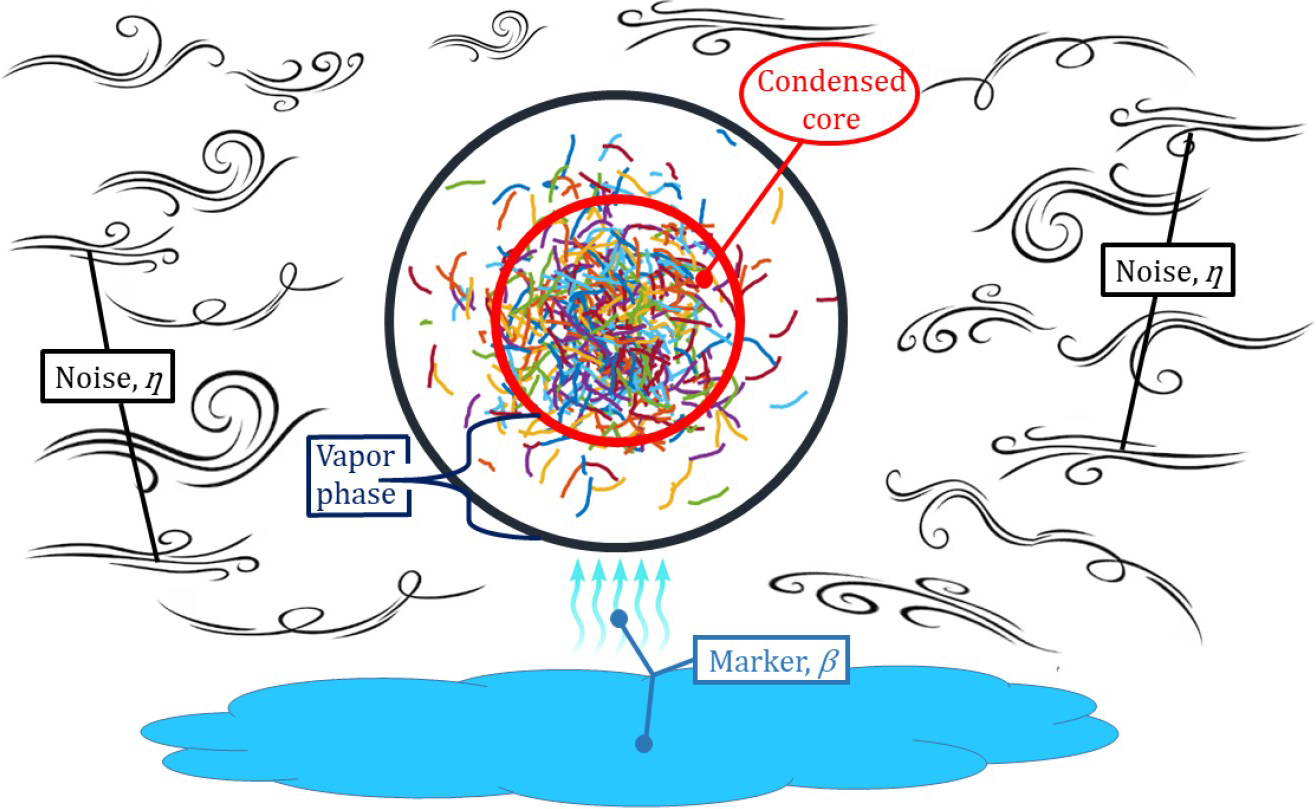
Nicholas Ouellette of Stanford University has performed many laboratory experiments on swarms [11, 12]. He and his colleagues raised midges in enclosed, transparent boxes under controlled conditions of illumination and temperature. At appropriate times and light settings, the flies’ knee-jerk responses to markers triggered rapid swarm formation. Swarming insects seem to experience a central force in an approximately harmonic potential [11]. Even when enclosed in a cage, a swarm does not fill it; instead, it adopts the form of a “condensed core” surrounded by a “vapor” of insects that move in and out of the core [12] (see Figure 1 and Animation 1).

Scientists typically study collective animal motion by adapting the methodology of statistical mechanics and phase transitions to appropriate models [10]. The best-known example is the Vicsek model (VM), which is considered the paradigm of dry active matter physics [5]. It consists of \(N\) particles (the “animals”) with positions \(\mathbf{x}_i(t)\) and velocities \(\mathbf{v}_i(t)\) where \(|\mathbf{v}_i(t)|=v_0\); these variables are updated at discrete times according to the rule

\[\begin{eqnarray} \mathbf{x}_i(t+1)&=&\mathbf{x}_i(t)+\mathbf{v}_i(t+1), \quad i=1,...,N, \\ \mathbf{v}_i(t+1)&=& v_0\mathcal{R}_\eta\bigg[\Theta\bigg(\sum_{|\mathbf{x}_j-\mathbf{x}_i|<R_0} \mathbf{v}_j(t)-\beta\mathbf{x}_i(t)\bigg)\bigg]. \end{eqnarray} \tag1\]

Here, \(\Theta(\mathbf{x})=\mathbf{x}/|\mathbf{x}|\) and \(\mathcal{R}_\eta(\mathbf{w})\) performs a random rotation that is uniformly distributed on a spherical sector around \(\mathbf{w}\) with maximum opening \(\eta\) (strength of the alignment noise). At each time, particles align their velocities with the mean velocity of all particles within their sphere of influence, which has radius \(R_0\) plus noise. In the original VM, the particles are confined to a box with periodic boundary conditions and \(\beta=0\) in \((1)\) [5]. At a critical noise, the periodic VM undergoes an ordering phase transition; when \(\eta>\eta_c\), the average velocity of all particles is \(0\) (it is nonzero when \(\eta<\eta_c\)).

The macroscopic quantities that obey power laws at the phase transition include correlation length, correlation time, and susceptibility. We can calculate these quantities from the dynamic correlation function (DCF) and static correlation function (SCF) [1]:

\[C(r,t)= \Biggl \langle \frac{ \sum_{i=1}^N \sum^N_{j=1}\delta\hat{\mathbf{v}}_i(t_0)\cdot\delta\hat{\mathbf{v}}_j(t_0+t)\delta[r-r_{ij}(t_0,t)]}{\sum^N_{i=1}\sum^N_{j=1}\delta[r-r_{ij}(t_0,t)]} \Biggr \rangle_{t_0} , \quad C(r)=C(r,0).\tag2\]

Fluctuating normalized velocities \(\delta\hat{\mathbf{v}}_i\) and positions \(\mathbf{r}_i(t)\) are measured with respect to the center of mass, and \(r_{ij}(t_0,t)=|\mathbf{r}_i(t_0)-\mathbf{r}_j(t_0+t)|\). Averages \(\langle f\rangle_{t_0}\) are over time and different random initial conditions [9]. The correlation length \(\xi\) is the first \(0\) of the SCF. Equivalently, we can calculate the maximum of its integral \(Q(r)\), where \(\xi=\textrm{argmax}_r Q(r)\); \(\chi=Q(\xi)\) is the susceptibility. In a phase transition at \(N=\infty\), \(\xi\) and \(\chi\) tend to infinity as power laws: \(\xi \sim |\eta-\eta_c|^{-\nu}\) and \(\chi\sim|\eta-\eta_c|^{-\gamma}\) where \(\nu\) and \(\gamma\) are static critical exponents.

We used these definitions to calculate macroscopic quantities from both movies of natural swarms and numerical simulations of mathematical models. How is this possible? Doing so clearly requires some sort of extrapolation procedure, as we cannot film infinitely many flies or set \(N=\infty\) in our numerical simulations. Fortunately, the critical parameter \(\eta_c(N)\) for finite \(N\) is such that the correlation length is proportional to \(N^{1/3}\) for all sufficiently large \(N\). In the jargon of phase transitions, correlations are scale free. SCF and DCF then depend on the control parameters (e.g., \(\eta\)) only through correlation length, in what is known as the finite-size scaling hypothesis. This hypothesis allows us to extrapolate power laws of macroscopic variables for finite \(N\) to the case of infinitely many particles in order to characterize phase transitions [10]. 

However, based on movies of swarms, \(\nu=0.35 \pm 0.10\) and \(\gamma=0.9 \pm 0.2\); from the periodic VM, \(\nu =0.75 \pm 0.02\) and \(\gamma=1.6 \pm 0.1\) [1]. No agreement. Even worse, the swarm should uniformly fill the periodic box at criticality, which is not what happens in Figure 1. Another important quantity, the dynamical critical exponent \(z\), is also quite different in measurements versus simulations of the periodic VM [3, 4]. We define \(z\) via the dynamic scaling hypothesis for the normalized correlation \(g(t)=\hat{C}(k,t)/\hat{C}(k,0)\), where \(\hat{C}(k,t)\) is the spatial Fourier transform of the DCF in \((2)\) [3]. When \(k=k_c=1/\xi\) and \(g(t)\) is written as a function of \(k^z_ct\), data for different \(N\) collapse to a single curve for numerical simulations of the periodic VM and other periodic models near their ordering transitions [3, 4]. The models that are close to these transitions are invariant under translation, meaning that markers are ignored. Cavagna’s renormalization calculations and numerical simulations yield \(z=1.35\) (close to a measured value), but their static critical exponents \(\nu=0.748\) and \(\gamma = 1.171\) are far from measurements [4].

Real insects do not like being confined by an imaginary periodic box, which is why we include the confining parameter \(\beta>0\) in \((1)\). Much like observations [12], the resulting swarms have condensed cores and vapors of insects (as in Figure 1). Numerical simulations exhibit many time-dependent periodic, quasiperiodic, and chaotic attractors that are not present in the periodic VM. Chaos is characterized by a positive largest Lyapunov exponent that indicates sensitivity to initial conditions [9]. Surprisingly, several scale-free lines exist in the noise confinement \((\eta, \beta)\) plane on which the macroscopic quantities are functions of \(\xi\) only. This hallmark of criticality indicates that macroscopic quantities are power laws in the control parameter: either \(\beta\) or \(\eta\). Figure 2 depicts the region near the origin of the \((\eta, \beta)\) plane with two of these critical lines for finite \(N\). The lines \(\beta_c\) and \(\beta_0\) respectively separate single-cluster from multi-cluster chaos [9] and chaos from non-chaos [8]. Topological data analysis helps us identify \(\beta_c\) [9].

As \(N\rightarrow\infty\), the aforementioned lines tend towards the horizontal axis \(\beta=0\) at the same rate and produce the same set of critical exponents for different values of \(\eta\) [9]. The horizontal axis is a line of critical points for the scale-free chaos phase transition, which is quite different from other known phase transitions and remains largely unexplored. Studies of the quasiperiodic route to chaos focus on special low-dimensional maps and irrational numbers—such as the golden mean—that are poorly approximated by rationals. We do not know how these routes change as the number of particles increases, or whether correlation functions such as \((2)\) play a significant role.

What are the values of the critical exponents? Asymptotic methods allow us to calculate them for the mean-field version of the VM. Assuming that all particles occupy the same point at all times, this mean-field point obeys \((1)\) with \(N=1\). The mean-field critical exponents are \(\nu=0.5\), \(\gamma=1\) (as in the Landau theory of equilibrium phase transitions [10]), and \(z=1\) [7]; there is no theory for the general case. We fix \(\eta\) and calculate \(\xi\), \(\chi\), and \(g(t/\xi^z)\) as functions of \(\beta_c\) or \(\beta_0\) for increasing values of \(N\). Then, we fit lines in log-log planes by least squares (LS) to obtain the critical exponents. Scaling the time in the DCF as \(g(t/\xi^z)\) partially collapses this function for \(0<\xi^{-z}t<4\) [8, 9] (see Figure 2). By using the line \(\beta_c\), we find that \(\nu=0.439 \pm 0.009\), \(\gamma=0.92 \pm 0.05\), and \(z=1.01 \pm 0.01\) [9]. The largest Lyapunov exponent decreases to \(0\), with \(\beta\) as a power law with exponent \(\varphi=z\nu\). The static exponents \(\nu, \gamma\) are close to those in natural swarms [1], but the dynamic exponent \(z\) is not [3, 4]. Measurements of \(z\) in natural swarms are peculiar because its value depends on the fitting procedure. With LS, \(z_{\textrm{LS}}=1.16\pm 0.12\); with reduced major axis (RMA) regression, \(z_{\textrm{RMA}}=1.37\pm 0.11\) [4]. During LS fitting, the \(x\) coordinate should be exact and the \(y\) coordinate corresponds to measurements with inherent error. In RMA fitting, however, both \(x\) and \(y\) are measured quantities with corresponding errors. Nevertheless, both fitting procedures yield the same values for data from numerical simulations. What is going on?

The movies of midge swarms that we used to calculate critical exponents have different durations and were taken on different days under different environmental conditions (different noise). Furthermore, the swarms comprise vastly fluctuating numbers of insects, often from different species. To mimic these variations, we postulate that swarms occupy the criticality region between the critical lines in Figure 2. First, we gather a mixture of data from numerical simulations of \((1)\) on lines \(\beta_c\) and \(\beta_0\) for different values of \(\eta\) and \(N\). We then use LS and RMA to fit the resulting mixed data, thereby obtaining \(z_\textrm{LS}=1.15 \pm 0.11\) and \(z_\textrm{RMA}=1.33\pm 0.10\). By fixing \(N=500\) and varying the noise on the \(\beta_c\) and \(\beta_0\) critical lines, we find that \(z_\textrm{LS}=1.24 \pm 0.11\) and \(z_\textrm{RMA}=1.37\pm0.10\) [8]. These values have excellent agreement with the measured values of \(z\), \(\nu\), and \(\gamma\) in natural swarms. In addition, the DCF \(g(t)\) collapses only for small values of \(t/\xi^z\) (see Figure 2); measurements of \(g(t)\) in natural swarms exhibit the same partial collapse [3]. For the confined VM, this collapse may indicate that the chaotic dynamics occur on several time and length scales, possibly due to the multifractal nature of the attractors [8, 9]. In a curious twist, the deterministic confined VM has exact periodic and quasiperiodic solutions for quantized values of the confinement that resemble Bohr’s circular orbits in his atomic model and may yet be relevant for the transition to chaos [2]. 

Further mathematical studies of the phenomena from our work can introduce new fields of research. Exploring these phase transitions and their relation to swarms is a fascinating endeavor in the scientific realms that intersect mathematics, physics, and biology.

References
[1] Attanasi, A., Cavagna, A., Del Castello, L., Giardina, I., Melillo, S., Parisi, L., … Viale, M. (2014). Finite-size scaling as a way to probe near-criticality in natural swarms. Phys. Rev. Lett., 113(23), 238102.
[2] Bonilla, L.L., & González-Albaladejo, R. (2025). Exact solutions of the harmonically confined Vicsek model. Chaos Solit. Fractals, 191, 115826.
[3] Cavagna, A., Conti, D., Creato, C., Del Castello, L., Giardina, I., Grigera, T.S., … Viale, M. (2017). Dynamic scaling in natural swarms. Nat. Phys., 13(9), 914-918.
[4] Cavagna, A., Di Carlo, L., Giardina, I., Grigera, T.S., Melillo, S., Parisi, L., … Scandolo, M. (2023). Natural swarms in 3.99 dimensions. Nat. Phys., 19(7), 1043-1049.
[5] Chaté, H. (2020). Dry aligning dilute active matter. Annu. Rev. Condens. Matter Phys., 11, 189-212.
[6] Downes, J.A. (1969). The swarming and mating flight of Diptera. Annu. Rev. Entomol., 14(1), 271-298.
[7] González-Albaladejo, R., & Bonilla, L.L. (2023). Mean-field theory of chaotic insect swarms. Phys. Rev. E, 107, L062601.
[8] González-Albaladejo, R., & Bonilla, L.L. (2024). Power laws of natural swarms as fingerprints of an extended critical region. Phys. Rev. E, 109, 014611.
[9] González-Albaladejo, R., Carpio, A., & Bonilla, L.L. (2023). Scale-free chaos in the confined Vicsek flocking model. Phys. Rev. E, 107, 014209.
[10] Huang, K. (1987). Statistical mechanics (2nd ed.). New York, NY: Wiley.
[11] Kelley, D.H., & Ouellette, N.T. (2013). Emergent dynamics of laboratory insect swarms. Sci. Rep., 3(1), 1073.
[12] Sinhuber, M., & Ouellette, N.T. (2017). Phase coexistence in insect swarms. Phys. Rev. Lett., 119(17), 178003.