Learning in Image Reconstruction: A Cautionary Tale

The growing influence of learning methods across science, industry, and society has generated significant interest in image reconstruction and inverse problems. This research area constitutes one of the most important interfaces between mathematics and a wide range of scientific and industrial domains, including medicine, materials testing, remote sensing, and astronomy. Despite the notorious difficulties that are caused by the mathematical ill-posedness of inverse problems, several examples have exhibited striking performance in recent years. Here, we highlight some associated questions of reliability and trustworthiness for learning algorithms.

The seemingly innocent formulation of an inverse problem is commonly stated as

\[y=A(x) + \varepsilon,\]

where \(x \in \mathcal{X}\) denotes the quantity of interest, \(A\) denotes a forward operator that encodes the measurement process, and \(y \in \mathcal{Y}\) denotes the observed measurement data (with noise \(\varepsilon\)). Solving this inverse problem involves the retrieval of \(x\) given data \(y\). To clarify, let us focus on X-ray computed tomography (CT) for medical imaging. In this context, \(A\) is the Radon transform, \(y\) is the sinogram, and \(x\) is the density inside some part of the human body.

Johann Radon had already derived an exact inversion formula—called filtered back projection—about 50 years before the construction of the first CT scanner [8]. Although his method is still utilized today, filtered back projection yields less favorable results in realistic scenarios where measurements are only partially available and corrupted by errors due to technical constraints. To tackle these issues, the inverse problems community developed regularization methods [2] that can approximately recover the desired quantity \(x\) in situations where the direct inversion would produce unfavorable results.

In response to the increasing availability of datasets, novel developments in learning theory, and improved hardware resources, focus has now shifted towards data-driven methods. Typical approaches include end-to-end learning (directly from the given data or as a form of post-processing), unrolling, plug-and-play, learned regularization, and the use of diffusion models as priors in Bayesian inverse problems. While the reconstruction performance is often remarkable, we must also question the resilience of the employed models. For some reconstruction method \(F: \mathcal{Y} \rightarrow \mathcal{X}\), we would thus like to quantify the reconstruction error \(\mathcal{E}(y,x;F) := \|F(y)-x\|\) in some norm.

Our case concerns a parametrized method \(F_\theta\), where the parameters \(\theta\) are typically the weights of a neural network. For supervised learning, we utilize a dataset of input-output pairs \(\mathcal{T} = \{(x_1,y_1),...,(x_N,y_N)\}\); we typically assume that the pairs are independent and identically distributed with respect to an unknown data distribution \(\pi\). Learning the reconstruction method \(F_\theta\) involves finding parameters \(\theta\) that minimize the loss \(\mathcal{L}(\theta)=\Sigma_{(x,y)\in\mathcal{T}}\mathcal{E}(y,x;F_\theta)\). Because we can solve the optimization problem reasonably well, the key quality indicator is the so-called generalization behavior, which measures the method’s performance on unseen data.

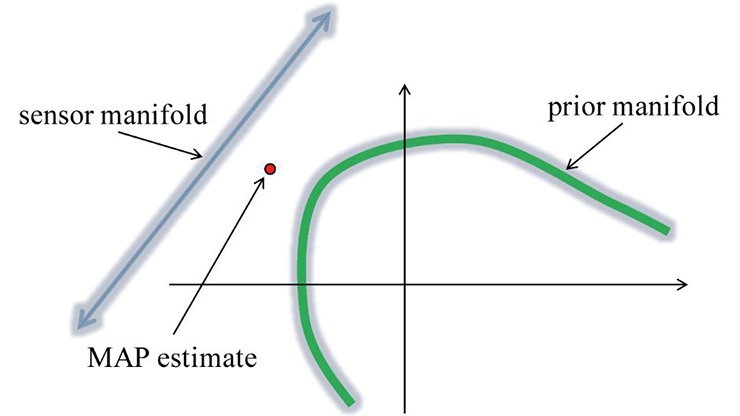
To test this property, we usually employ a validation dataset \(\tilde{\mathcal{T}}\) that is disjoint from the training dataset. The first obvious but core issue is as follows: What if the dataset does not capture the desired distribution \(\pi\)?

While it is important to note that learned methods can provide functionality beyond memorization of the dataset, the quality of the data plays a crucial role in the learning process. In medical imaging, datasets consist of numerous high-resolution images and scans. What happens if certain structures (pathologies) are not present in the training or validation dataset but appear with low probability in the desired distribution \(\pi\), which includes real-life diagnosis scenarios?

We explore this question for limited-angle CT, where \(A\) is the Radon transform with a restricted range of available angles \([0,\pi/2]\). The reconstruction method first applies a direct reconstruction (generalized inverse of the forward operator \(A\)) before employing a neural network \(f_\theta\) with a state-of-the-art U-Net architecture [9]. To obtain an understandable training set, we randomly sample ellipses on the domain \([0,1]^{\times 2}\) as targets \(x_i\) and their limited-angle sinograms with additive noise as inputs \(y_i\).¹

Figure 1 illustrates the output of the direct reconstruction and the learned U-Net. Although the specific ellipse in Figures 1a and 1b was not part of the training data, the network greatly suppresses artifacts and even recovers structures in places where the necessary information was absent from the data. However, Figures 1c and 1d depict the unsatisfactory results when we apply the network to structures that were absent from the training data. Missing structures or biases in the dataset therefore transfer to out-of-distribution (OOD) data [6].

Practitioners face two key problems in this setting: the reconstruction of the rectangle in Figure 1c (which is OOD) does not attain the desired result, and the output of the network is a very reasonable image — meaning that even experts often cannot recognize the artifacts. In addition to missing pathologies, this effect can create hallucinations (i.e., structures that are completely fabricated by the network). Researchers are investigating these hallucinations for far more complex scenarios, such as magnetic resonance imaging scans of brains [7]. Such cases are rare but critical and call for both OOD detection and uncertainty quantification (UQ). This problem inspires a second important question: Can we ever quantify the reconstruction error?

Recent studies use hallucinations to demonstrate the lack of meaningful error estimates in the context of medical imaging [1, 3, 5, 7]. To accentuate this issue, we construct adversarial examples [10]: small perturbations of regular inputs that yield catastrophic failure cases. For the same network as before, doing so amounts to solving the following problem:

\[\underset{\varepsilon\in B_\delta}{\max}\|f_\theta(A^+(y+\varepsilon))-x\|^2_2,\]

where \(x\) is now an in-distribution input (i.e., an ellipse) and \(y\) is the corresponding Radon transform. The adversarial noise \(\varepsilon\) is restricted to having a small \(\ell^2\)-norm, namely \(\|\varepsilon\|_2/(N\cdot K) \le \delta= 0.0006\); here, \(N\) denotes the width of the image and \(K\) is the number of angles.

Figure 2 displays increased noise artifacts for direct reconstruction, though it still carries some interpretable information. The learned model output is completely corrupted, however, with densities that are close to zero and no observable structure whatsoever. Although this example employs a toy setup for illustrative purposes, it aligns with the findings of various studies [5], highlights the difficulty of providing error estimates, and accentuates the potential risk of certain learning methods for ill-posed inversion. We intend for this scenario to serve as a cautionary tale and a call to action, rather than a deprecation of learning methods.

Various advancements can outperform the employed end-to-end architecture \(F_\theta =f_\theta \circ A^+\) in terms of both performance and resilience. Furthermore, OOD detection and UQ are emerging as extremely relevant topics that can mitigate the severity of hallucinations. The robustness of neural networks is already positioned as a leading issue for learning, and theoretical understanding—especially in the context of inverse problems—is continuing to grow [4]. To conclude, data-driven methods exhibit enormous potential for improved image reconstruction but will only be of real use if they can prove their resilience and lack of hallucinations; artifacts should be clearly detectable and uncertainties should be quantifiable. This objective calls for a paradigm shift in the development of these methods to focus on UQ and behavior in critical cases, rather than seemingly impressive results for favorable cases.

¹ The source code for the experiment is available online.

References
[1] Antun, V., Renna, F., Poon, C., Adcock, B., & Hansen, A.C. (2020). On instabilities of deep learning in image reconstruction and the potential costs of AI. Proc. Natl. Acad. Sci., 117(48), 30088-30095.
[2] Benning, M., & Burger, M. (2018). Modern regularization methods for inverse problems. Acta Numer., 27, 1-111.
[3] Bhadra, S., Kelkar, V.A., Brooks, F.J., & Anastasio, M.A. (2021). On hallucinations in tomographic image reconstruction. IEEE Trans. Med. Imaging, 40(11), 3249-3260.
[4] Burger, M., & Kabri, S. (2024). Learned regularization for inverse problems: Insights from a spectral model. Preprint, arXiv:2312.09845v2.
[5] Gottschling, N.M., Antun, V., Hansen, A.C., & Adcock, B. (2024). The troublesome kernel — On hallucinations, no free lunches and the accuracy-stability trade-off in inverse problems. Preprint, arXiv:2001.01258v4.
[6] Hong, Z., Yue, Y., Chen, Y., Cong, L., Lin, H., Luo, Y., … Xie, S. (2024). Out-of-distribution detection in medical image analysis: A survey. Preprint, arXiv:2404.18279v2.
[7] Muckley, M.J., Riemenschneider, B., Radmanesh, A., Kim, S., Jeong, G., Ko, J., … Knoll, F. (2021). Results of the 2020 fastMRI challenge for machine learning MR image reconstruction. IEEE Trans. Med. Imaging, 40(9), 2306-2317.
[8] Radon, J. (1917). Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten. Ber. Verh. Säch. Akad. Wiss., 69, 262-277.
[9] Ronneberger, O., Fischer, P., & Brox, T. (2015). U-Net: Convolutional networks for biomedical image segmentation. In N. Navab, J. Hornegger, W. Wells, & A. Frangi (Eds.), Medical image computing and computer-assisted intervention — MICCAI 2015 (pp. 234-241). Lecture notes in computer science (Vol. 9351). Cham, Switzerland: Springer.
[10] Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., & Fergus, R. (2014). Intriguing properties of neural networks. Preprint, arXiv:1312.6199v4.