Leveraging Noise to Control Complex Networks

From the diffusion of molecules in a living cell to fluctuations in population levels within an ecosystem, stochasticity pervades our world. When coupled with the inherent nonlinearity of these systems, even small amounts of stochasticity (or “noise”) can generate macroscopic, potentially deleterious outcomes. For example, noise in the expression of genes within a genetic regulatory network can spontaneously change the phenotypes of cancer cells, which might complicate therapeutic strategies targeting particular cell types [4]. Similarly, fluctuations in the populations of key species can propagate throughout a food web, potentially leading to the extinction of other species [5]. Given these far-reaching consequences, it is perhaps surprising that noise has been regarded as little more than a nuisance in the development of methods to control real network systems like those above. Here we take a different approach by illustrating ways through which noise can be accounted for, and in fact exploited, to control network dynamical systems.

A key feature of many network dynamical systems is multistability—the presence of multiple stable states (stable fixed points and/or more general attractors). These states each represent distinct dynamical states that are persistent to small perturbations and in which the system could remain permanently in the absence of noise. In many cases, the noisy dynamics of a nonlinear dynamical system can be modeled as a system of stochastic ordinary differential equations, which in the simplest form is

$$dx=F(x;\mathrm{\Omega })dt+\sqrt{\epsilon }dW,$$

where $\mathrm{\Omega }$ are the system parameters and $dW$ s Gaussian noise. The dynamics of this noisy system are actually quite conceptually simple: the system will fluctuate within the basin of a particular attractor for a length of time until suddenly transitioning to another attractor. When this transition takes place, it will occur in a way that should be intuitive for any hiker—the system is most likely to transition by going through a “mountain pass,” or saddle point that connects the two attractors. Therefore, the dynamics of a noisy, multistable system can be distilled into a continuous time Markov chain R, where the strength of the noise $\epsilon$ and the heights of the “mountain passes” determine the rates of transition between different stable states. Such a Markov chain approach can capture the dynamics of any noisy multistable system regardless of its dimensionality, and has been applied to model, for example, chemical reactions and the folding dynamics of proteins [7].

What needs to be determined, then, is how to calculate the transition rates between stable states. This question was first considered rigorously for gradient systems (where $F(x;\mathrm{\Omega })=-\mathrm{\nabla }V(x;\mathrm{\Omega })$, for some $V$), which led to the celebrated Eyring-Kramers law:

$$k_{i,j}\propto \exp [(V{x}_i^{\ast };\mathrm{\Omega })-V(z_{i,j}^{\ast };\mathrm{\Omega }))/\epsilon$$

where $k_{i,j}$ is the transition rate from attractor $x_i^{\ast }$ to attractor $x_j^{\ast }$, and $z_{i,j}^{\ast }$ is the location of the highest saddle point on the path separating the two attractors. Determining the rates $k_{i,j}$ either analytically or numerically is the focus of much of the field of transition state theory [3].

The situation is more involved in nongradient systems, where no potential exists. In these systems, the transition rates $k_{i,j}$ between attractors $x_i^{\ast }$ and $x_j^{\ast }$ can be approximated by employing  the Wentzell-Freidlin theory [2], giving

$$k_{i,j}\propto \exp [-S_{i,j}^{\ast }(\mathbf{\Omega }\mathbf{)}\mathbf{/}\epsilon \mathbf{]}\mathbf{,}\mathbf{w}\mathbf{h}\mathbf{e}\mathbf{r}\mathbf{e}$$

$$\begin{gathered} S_{i,j}^{\ast }(\mathrm{\Omega })=\underset{\begin{array}{c}\varphi (t)\\ \varphi (-\mathrm{\infty })=x_i^{\ast }\\ \varphi (\mathrm{\infty })=x_j^{\ast }\end{array}}{min} \\ \left(\frac{1}{2}{\int }_{\mathrm{\infty }}^{-\mathrm{\infty }}{\Vert \frac{d\varphi }{dt}(t)-F(\overrightarrow{\varphi }(t);\mathrm{\Omega })\Vert }^{2}dt\right) \end{gathered}$$

Above, $S_{i,j}^{\ast }(\mathbf{\Omega })$ is the is the Wentzell-Freidlin action evaluated along the minimum action path, ${\varphi }^{\ast }(t)$. For small noise levels, this path will be the most probable path a noise induced transition will follow. In general, $S_{i,j}^{\ast }$ can only be calculated numerically, but many good algorithms are available to do so [1].

Up to this point we have discussed how network dynamical systems are quite often multistable, how noise can induce transitions between different attractors in these systems, and how the deterministic dynamics $F(x;\mathrm{\Omega })$ can be employed to calculate the rates of these transitions. Intuitively, then, if we change the system dynamics—by altering the parameters $\mathrm{\Omega }$, for example—we can change the transition rates. This, in turn, modifies the dynamics of the Markov chain and could alter its stationary distribution, i.e., the fraction of time spent close to each stable state in the long time limit. What about the inverse problem: how should the tunable parameters of a system be altered to drive the dynamics of our Markov chain to converge to a specific stationary distribution? In particular, we seek to alter the parameters $\mathrm{\Omega }$ of the noisy dynamical system to reshape the topography of the attractor landscape and thus induce desired transitions, as illustrated schematically in Figure 1.

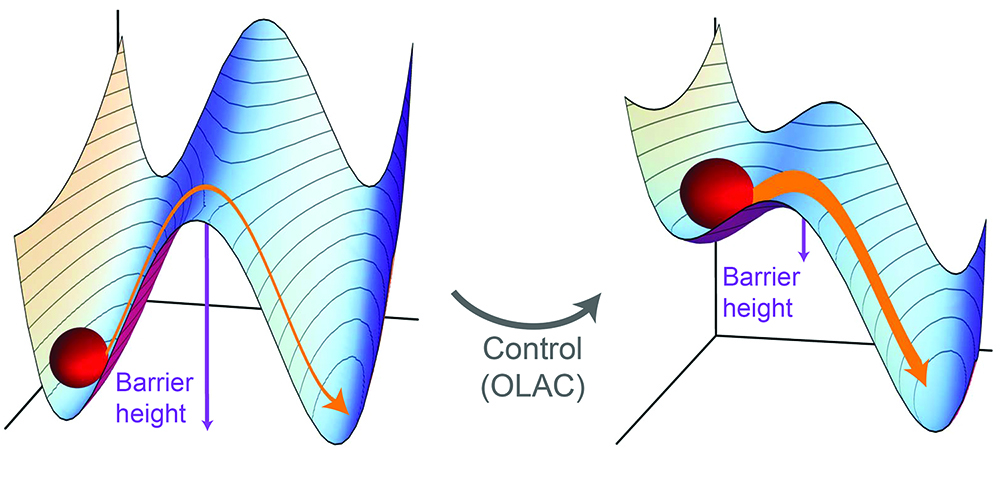
One way to address this question is by identifying an appropriate objective functional on the space of Markov chains parameterized by $\mathrm{\Omega }$, denoted $G(\mathbf{R}(\mathrm{\Omega }))$ whose maximum corresponds to the desired stationary distribution of $G$. This could, for example, be the limiting (long-time) occupancy of a particular stable state of interest. Looking for parameters that achieve this therefore reduces to another optimization problem, now over the system parameters, of the form 

$$\underset{\begin{array}{c}\mathrm{\Omega }\in \mathbf{U}\end{array}}{max}G(\mathbf{R}(\mathrm{\Omega })),$$

where $\mathbf{U}$ denotes the set of possible parameter choices. This problem can be solved numerically using standard algorithms and packages [6]. The combined algorithm, which synthesizes techniques for estimating transition rates between attractors with methods to maximize objective functionals, is termed Optimal Least Action Control (OLAC) [8].

Using OLAC, we can control the response to noise in network dynamical systems with hundreds of variables and thousands of parameters. For example, we have successfully applied this methodology to high-dimensional network models from systems biology and computational neuroscience. One of the lessons we have extracted from these applications is that, when transitions from one stable state to another are optimized, the most likely transition path connecting them often passes through an intermediate stable state. This phenomenon can occur even in systems with a large number of variables, and suggests that “indirect” control strategies—inducing transitions to undesired states as a means to achieve transitions to desired ones—may actually be effective in network dynamical systems.

Other results are also intriguing. For example, when we augmented OLAC with constraints of the form $\sum _i(|\mathrm{\Delta }{\mathrm{\Omega }}_i|)\le \beta$ known to generate sparsity in many generic optimization scenarios [6], the resulting control interventions often required manipulation of fewer than 10% of all parameters. This suggests that it might be possible to control the response to noise in systems using only a handful of carefully picked parameters, which promises to be especially advantageous in connection with experimental implementations. The question of just how small this set can be for a given control problem remains open.

Ultimately, this work demonstrates that noise, far from being a nuisance, can actually be a tool that allows for the shaping of system dynamics even when other forms of control are not possible. The method we propose as such an approach, OLAC, relies on the fact that a noise-induced transition will typically only follow a single optimal path from one attractor to the other. This observation allows us to reduce the dynamics of an arbitrarily high-dimensional system into a sequence of one-dimensional paths, and in turn into a computationally-tractable, continuous time Markov chain that captures the essence of the dynamics. In general, the study of how to effectively control high-dimensional, noisy, nonlinear dynamical systems (as is common in the case of real network systems) is in its infancy, and this area promises to be an exciting one in years to come.

This article describes results of our recent paper [8], which provides substantially more details about OLAC along with example applications and relevant references.

References

[1] E, W., Ren, W., & Vanden-Eijnden, E. (2004). Minimum action method for the study of rare events. Comm. Pure Appl. Math., LVII, 1–20.
[2] Freidlin, M.I. & Wentzell, A.D. (1979). Random Perturbations of Dynamical Systems. New York, NY: Springer-Verlag.
[3] Gardiner, C. (2009). Stochastic Methods. Berlin: Springer-Verlag.
[4] Gupta, P.B., Fillmore, C.M., Jiang, G., Shapira, S.D., Tao, K., Kuperwasser, C., & Lander, E.S. (2011). Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell, 146, 633–644.
[5] Lande, R., Engen, S., & Saether, B. (2003). Stochastic Population Dynamics in Ecology. Oxford: Oxford University Press.
[6] Nocedal, J. & Wright, S.J. (2006). Numerical Optimization. New York, NY: Springer.
[7] Rao, F. & Caflisch, A. (2004). The protein folding network. J. Mol. Biol., 342, 299–306. 
[8] Wells, D.K., Kath, W.L., & Motter, A.E. (2015). Control of stochastic and induced switching in biophysical complex networks. Phys. Rev. X, 5, 031036.