Mathematical Modeling and Optimization in Cryobiology

The first successful cryopreservation of human spermatozoa occurred in 1954; the mid-1980s then saw success with embryos and oocytes. More recently, cryopreservation has played an increasingly important role in processes like assisted reproduction and in vitro fertilization (IVF). Concurrent to these successes, major efforts have investigated the fundamental, medical, clinical, practical, legal, and ethical aspects of IVF. The latest evidence suggests that survival rates of cryopreserved human sperm, oocytes, and embryos vary broadly — ranging from the flip of a coin (50 percent) to near-complete success (98 percent). Methodologies are similarly variable in terms of thermal protocols for cooling and warming as well as the choice(s) of cryoprotectant: the chemical “antifreeze” that inhibits intracellular ice formation and induces intracellular dehydration and vitrification.

While scientists have applied IVF to certain laboratory animals, livestock, and fish species, only recently have they sought to establish even basic guidelines for IVF protocols in wild animals. In the case of rare and endangered species, for instance, samples are simply too precious to risk failure; IVF is thus not an option.

Cryopreservation of larger-scale biospecimens like corneas, articular cartilage tissue, and ovarian tissue is complicated by their size, complex shapes, and the presence of vascular and layered structures. However, such preservation is particularly important for organ transplantation and other medical purposes like biobanking and personalized medicine. In bone marrow transplantation, for example, the preservation of human platelets is crucial. After chemotherapy, patient blood contains an insufficient number of platelets, which results in a high risk of potentially fatal internal bleeding. There is hence an undeniable need for effective long-term freezing and thawing protocols and the personal banking of human platelets. Furthermore, cryopreserved arteries offer hope for a limitless supply of long-lasting arterial conduits for bypass grafts but face the barrier of structural failures due to thermal stresses during cooling and warming. A lack of understanding of arteries’ thermal and mechanical properties makes it difficult to predict or prevent failures. Despite significant progress, it is clear that we still must investigate optimal cryofreezing and thawing procedures across a vast expanse of sample types and sizes.

During the cryopreservation process, ice nucleation can damage biological samples [6]. The addition of cryoprotective agents (CPAs) to the solution in which the sample is frozen may counteract this issue. Common CPAs include glycerol, ethylene glycol, and dimethyl sulfoxide; some of these permeate into the sample, while others do not. Permeating CPAs act like antifreeze, lowering the freezing point and inhibiting ice nucleation. Non-permeating CPAs can help draw water out of the sample, which also reduces the risk of ice nucleation. 

While the benefits of CPAs have been known since 1949 [7], the path to successful cryopreservation of any biological sample is still fraught with danger. Cooling with too little CPA may cause ice nucleation, while CPA overexposure can give rise to a second damage mechanism that is sometimes called chemical toxicity. This tradeoff—known as the two-factor hypothesis [5]—creates a delicate balancing act. Given the immense diversity among biological samples that require cryopreservation, it is not surprising that different CPAs affect different types of samples in varied ways.

Much research and experimentation—often on the basis of an individual species and/or sample type—has attempted to identify the best type(s) and amount(s) of CPA to successfully cryopreserve a biological sample. Sample survivability also depends on the manner in which it is brought to the storage temperature. Certain tissues can be cooled at relatively high rates (e.g., -30°C/minute), while others respond better to a much slower cooling rate (e.g., -0.5°C/min) [2]. A slower cooling rate may reduce the chance of ice nucleation but increase the chemical/CPA exposure. Scientists can also cool samples in stages by gradually reducing them to an intermediate temperature (e.g., -80°C) and then transferring them into much colder liquid nitrogen (e.g., -196°C) for long-term storage, often via rapid plunge [8]. But cooling the sample is only half of the journey, as it eventually needs to be warmed. Warming protocols, analogous to cooling protocols but varied in their own unique ways, must melt any solidified material outside of the sample and can involve submerging the sample—possibly in multiple stages—into warm water/CPA/salt solutions to achieve a final, desired, revitalized state.

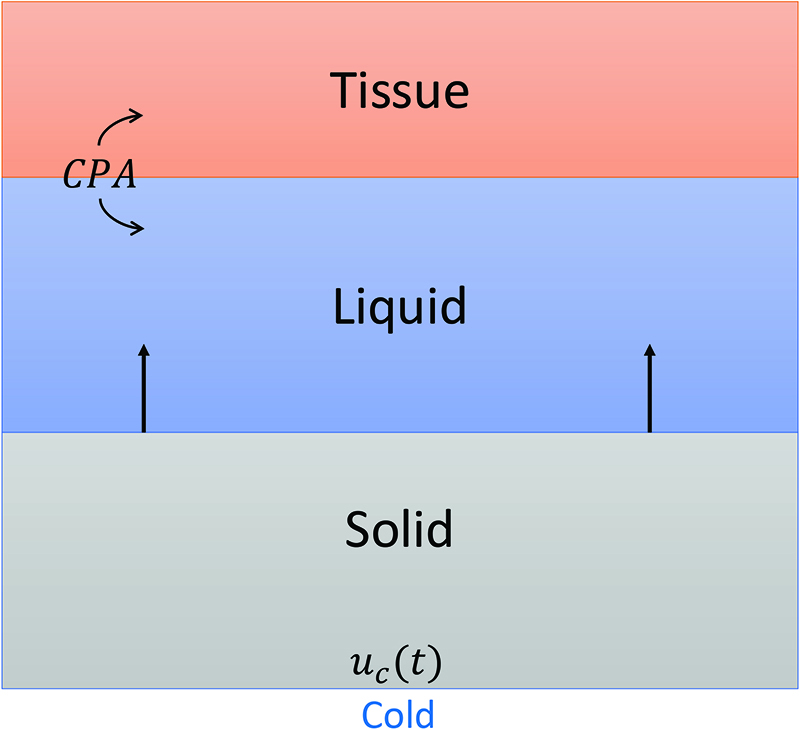
Many factors contribute to the development of a cryopreservation protocol and can affect preservation outcome, including thermal and chemical transport, phase change, the diversity of biological samples, and sample interaction with different CPAs. Mathematical modeling plays an essential role in understanding and exploring the relationships between these processes. In ongoing work, we have created a partial differential equation (PDE) model that represents thermal and chemical diffusion during the cooling phase of cryopreservation and are adapting it for PDE-constrained optimization.

Our model consists of three finite layers: solid, liquid, and tissue (see Figure 1). The external bottom boundary controls the cooling, and we are interested in assessing the tissue damage in the top layer. Initially, a liquid solution with a prescribed CPA concentration surrounds the tissue. Solidification begins as the external boundary cools, and diffusion extracts heat from the tissue through multiple layers and the external bottom boundary. The middle liquid layer comprises two evolving concentrations: one for the CPA (which can permeate into the tissue) and one for an extracellular salt (which cannot). Similarly, the tissue has a CPA concentration and an intracellular salt concentration (which also does not permeate). This mathematical framework allows us to specify a cooling protocol and chemical environment, as well as determine the corresponding response in the tissue.

We can frame our PDE system as an optimal control problem. We minimize a cost function \(J\)—which measures damage to the tissue—over a control function \(u_c(t)\) that describes the cooling protocol along an external boundary. Formally, we write

\[\min_{u_c(t)} J(u, u_c),\]

where the state variable \(u\) is the solution to the PDE system, expressed generically as

\[\mathcal{L}u = f.\]

Here, \(\mathcal{L}\) is a differential operator and \(f\) is some given data. The minimization is constrained by the PDE model, thus yielding a PDE-constrained optimization problem [4]. 

We can define the cost/damage function \(J\) in multiple ways. Two common proxies of relevance for tissue damage assessment are (i) undercooling—i.e., cooling the tissue below its freezing temperature—which depends on the amount of CPA in the tissue; and (ii) chemical toxicity in terms of CPA exposure. In the case of undercooling, we are specifically concerned with its implications in the ice nucleation process [6]. Our objective is to compute numerical solutions to the PDE-constrained optimization problem and derive a cooling protocol that causes as little damage as possible. In this example, we can monitor the tissue’s thermochemical state and assign a measure of potential damage given the thermal control at a boundary that is physically separated from the tissue by phase-evolving solid and liquid domains.

An important biopreservation goal—especially for larger tissues—is vitrification: the process of bringing a sample to an amorphous, or glassy, state without ice formation. Vitrification also involves cooling in the presence of CPAs but typically uses ultra-high cooling rates and/or high CPA concentrations to reach the glass transition temperature before freezing can occur. As with any cryopreservation scheme, this gauntlet must be run successfully in both directions. For example, the glass transition temperature is typically much lower than the freezing temperature; returning from a glassy state in way that does not trigger ice nucleation during warming is therefore a critical task. 

In response, we have framed the aforementioned cryopreservation process as a boundary control problem. Recent studies on the warming of vitrified tissues have explored the use of nanoparticles that are distributed through (typically larger) samples so that volumetric warming of the tissue can occur via an externally controlled magnetic field [3]. This type of heating can help prevent other damage modalities that pertain to significant thermal stresses, especially for the revitalization of larger tissues. Mathematically, we can frame this procedure as PDE-constrained optimization with internal controls.

The preservation of biological samples is extremely important to many aspects of healthcare, agriculture, the conservation of endangered species, and other scientific endeavors. Broad and successful efforts, such as the Pan-Smithsonian Cryo-Initiative for the preservation of biomaterials, are currently underway [1, 2]. However, the breadth of samples that require preservation means that the selection of an appropriate cryopreservation protocol may be complicated, expensive, and specialized to each sample type. We can employ mathematical modeling to streamline this process and better comprehend cryopreservation’s effects on these samples. Because the stakes are so high, even small clues for procedural improvements and gains in understanding can be very impactful. Applied mathematicians play a valuable role in building models of these complex biophysical systems and developing compatible, consistent optimal control schemes to inform experimentalists and practitioners who are furthering the goals of successful cryopreservation.

Anthony Kearsley delivered a minisymposium presentation about this research at the 2025 SIAM Conference on Computational Science and Engineering, which took place in Fort Worth, Texas, this past March.

References
[1] Comizzoli, P. (2014). C-29: The Pan-Smithsonian cryo-initiative — freezing for the future. Cryobiology, 69(3), 509.
[2] Comizzoli, P., Songsasen, N., Hagedorn, M., & Wildt, D.E. (2012). Comparative cryobiological traits and requirements for gametes and gonadal tissues collected from wildlife species. Theriogenology, 78(8), 1666-1681.
[3] Gangwar, L., Phatak, S.S., Etheridge, M., & Bischof, J.C. (2022). A guide to successful mL to L scale vitrification and rewarming. CryoLetters, 43(6), 316-321.
[4] Glowinski, R., Lions, J.-L., & He, J. (2008). Exact and approximate controllability for distributed parameter systems: A numerical approach. In Encyclopedia of mathematics and its applications (Vol. 117). Cambridge, U.K.: Cambridge University Press. 
[5] Mazur, P., Leibo, S.P., & Chu, E.H.Y. (1972). A two-factor hypothesis of freezing injury: Evidence from Chinese hamster tissue-culture cells. Exp. Cell Res., 71(2), 345-355.
[6] Morris, G.J., & Acton, E. (2013). Controlled ice nucleation in cryopreservation — a review. Cryobiology, 66(2), 85-92.
[7] Polge, C., Smith, A.U., & Parkes, A.S. (1949). Revival of spermatozoa after vitrification and dehydration at low temperatures. Nature, 164(4172), 666.
[8] Stewart, S., White, A., Ou, W., Liu, W., Nagashima, J., Songsasen, N., & He, X. (2024). Controlled ice nucleation with a sand-PDMS film device enhances cryopreservation of mouse preantral ovarian follicles. J. Med. Device, 18(4), 041007.