Mathematics + Infrared Technology = New Diagnostic Technique for Autism
Chances are you know someone with concerns about their toddler’s behavior. Their child may be shy and sweet, but have an unpredictable attitude. He or she might throw the worst temper tantrums, sometimes kicking and screaming inconsolably for an hour. The smallest changes in routine may throw him or her off. It is probably impossible to reason with the child when he or she is upset. Does this behavior simply indicate a bad case of the “terrible twos”? Should the child be allowed time to grow out of this phase? Or are these signs of autism spectrum disorder (ASD)?
ASD is a neurodevelopmental disorder that affects approximately one to two percent of the population. This means that a school bus full of children will typically have one or two kids with ASD. Symptoms usually appear in the first two years of life and impair a child’s ability to function socially. Although current treatments vary, most interventions focus on managing behavior and improving social and communication skills with the hope that the child will one day become an independent adult. Because the capacity for change is greater at a young age, early diagnosis and intervention ensure the best possible outcomes.
Mathematics as the New Microscope
Given the many benefits of timely detection and treatment, we are keen to help doctors more quickly and accurately diagnose ASD in children. Our group uses mathematics as a microscope to understand biology and medicine [1]. We build computer models to simulate the effects of various drugs [2-3] and apply mathematical techniques to analyze clinical data.
How can we utlize math to generate a new autism detection tool? We believe that mathematics can objectively distinguish behaviors of children with ASD from those of their neuro-typical counterparts. For instance, we know that visual exploration in patients with ASD is different from that in neuro-typical individuals. This knowledge motivated us to create a new ASD detection technique—based on network analysis—that distinguishes varied eye-gaze patterns [4].
Network-based Analysis for Eye-gaze Patterns
To develop our novel method, we first evaluated 40 four- or five-year-old children. Half of them had ASD, while the others were neuro-typical. We showed each participant 44 photographs of faces on a screen, which were integrated into an eye-tracking system (see Figure 1). The infrared device uses emission and reflection of waves from the iris to interpret and identify locations on the stimuli at which each child was looking.
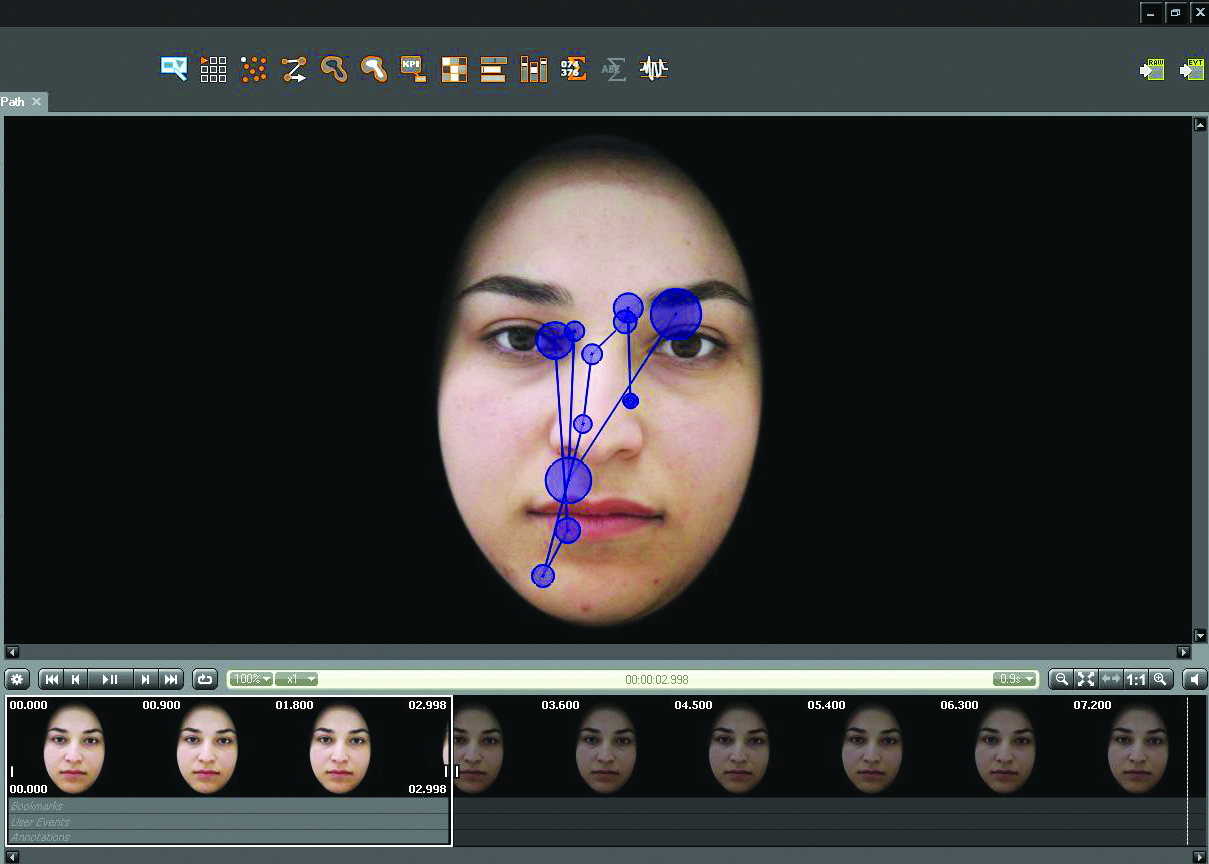
We then separated the images into seven key features, or areas of interest (AOI), on which participants focused their gaze: under the right eye, on the right eye, under the left eye, on the left eye, on the nose, on the mouth, and on other parts of the screen. We considered both a static measure—how much time each participant spent looking at each feature—and dynamic measures — how they moved their eyes and scanned the faces [4]. Children with ASD focus on and scan faces differently. For instance, when looking at a person’s face, neuro-typical children focus more on the eyes and those with ASD focus more on the mouth. This static measure is called “fixation time.” And when shifting their focus from someone’s eyes to their chin, neuro-typical children generally move their eyes more quickly and via a different path than children with ASD.
To investigate how ASD and neuro-typical children explore facial features in dissimilar ways, we employ the centrality concept from network analysis. Here, each of the seven AOIs acts as a node in our network model. Every saccadic transition between two AOIs yields a link connecting the two respective nodes. One can apply measures of centrality to assess the importance of each node. We computed the subsequent four centrality measures.
(i) Degree centrality—arguably the simplest conceptually—depicts the number of links associated or connected with a given node.
(ii) Betweenness centrality is the number of shortest paths between two additional nodes that pass through a given node. One can compute the betweenness of node \(k\) in \(G=(V;E)\) as follows:
\[B_k=\frac{\Sigma_{i,j\ne k}P_k(i,j)/P(i,j)}{\binom{N-1}{2}}, \]
where \(N\) is the number of nodes in the graph and \(P(i,j)\) denotes the number of shortest paths between nodes \(i\) and \(j\). Among these shortest paths, \(P_k(i,j)\) indicates how many pass through node \(k\).
(iii) Closeness centrality is another measure of a given node’s importance. One can calculate it from the reciprocal of the sum of the shortest paths’ length between the node and all other nodes in the graph. Closeness centrality quantifies the extent to which the network may be congested between a given pair of nodes:
\[C_k=\frac{N-1}{\Sigma_jd_{i,k}},\]
where \(d_{i,k}\) is the shortest path between nodes \(i\) and \(k\).
(iv) Eigenvector centrality assigns relative scores to all nodes in the network based on the concept that connections to high-scoring nodes contribute more to the score of the node in question than equal connections to low-scoring nodes. Specifically, the eigenvector centrality of node \(k\)—denoted \(E_k\)—is proportional to the weighted sum of the eigenvector centrality of the nodes to which it connects:
\[E_k=X_k^{\textrm{max}}=\frac{1}{\lambda^{\textrm{max}}}\Sigma_ja_{k,j}X_j^{\textrm{max}},\]
where \(\lambda^{\textrm{max}}\) is the largest eigenvalue related to the transition matrix \((a_{i,j})\) and \(X^{\textrm{max}}\) is the associated eigenvector.
A More Child-friendly Test for Early Autism Detection
Why do we want a new diagnostic technique for ASD? The hope is that a more child-friendly and improved diagnostic tool would facilitate early ASD detection in children. There is currently no definitive laboratory test or biomarker for the disorder. Assessment often includes a medical and neurological examination; an in-depth questionnaire about the child’s family history, behavior, and development; or an evaluation from a psychologist. In addition to being expensive, these diagnostic approaches are not toddler-friendly. Children will no doubt find it much easier to stare at faces than fill out questionnaires or undergo a psychological evaluation.
We hope that our network-based analysis will make the diagnostic process less stressful. Parents who suspect ASD in their toddlers can seek screening with our technology and have their children scan a few faces. If the results point to a high likelihood of ASD, the child can then undergo a more involved clinical appraisal.
Our group is mindful of the many benefits that accompany early ASD diagnosis and subsequent early intervention. Timely detection is associated with reduced parental stress, and prompt intervention is critical to achieving positive outcomes over time. Treatments implemented before age four are associated with significant gains in cognition, language, and adaptive behavior. Studies have similarly linked early interventions in ASD with improvements in daily living skills and social conduct.
By using mathematics to remove some of the barriers that inhibit early diagnosis, we hope that more children with ASD can receive timely intervention and attain a better quality of life and a higher degree of long-term independence.
References
[1] Layton, A.T. (2017). A new microscope for the kidney: mathematics. Am. J. Physiol. Renal Physiol., 312, F671-F672.
[2] Layton, A.T., & Vallon, V. (2018). SGLT2 inhibition in a kidney with reduced nephron number: modeling and analysis of solute transport and metabolism. Am. J. Physiol. Renal Physiol., 314, F969-F984.
[3] Leete, J., & Layton, A.T. (2019). Sex-specific long-term blood pressure regulation: modeling and analysis. Comp. Bio. Med., 104, 139-148.
[4] Sadria, M., Karimi, S., & Layton, A.T. (2019). Network centrality analysis of eye-gaze data in autism spectrum disorder. Comput. Bio. Med., 111, 103332.
About the Authors
Anita Layton
Canada 150 Research Chair, University of Waterloo
Anita Layton is the Canada 150 Research Chair in Mathematical Biology and Medicine and a professor of applied mathematics, computer science, biology, and pharmacy at the University of Waterloo in Canada. She leads a diverse and interdisciplinary team of researchers to use computational modeling tools to better understand aspects of health and disease.
Mehrshad Sadria
Ph.D. Candidate, University of Waterloo
Merhshad Sadria is a Ph.D. candidate in applied mathematics at the University of Waterloo. His research interests include mathematical modeling, computational biology, deep learning, and regenerative medicine.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



