Mathematics of Coupled Human-environment Systems

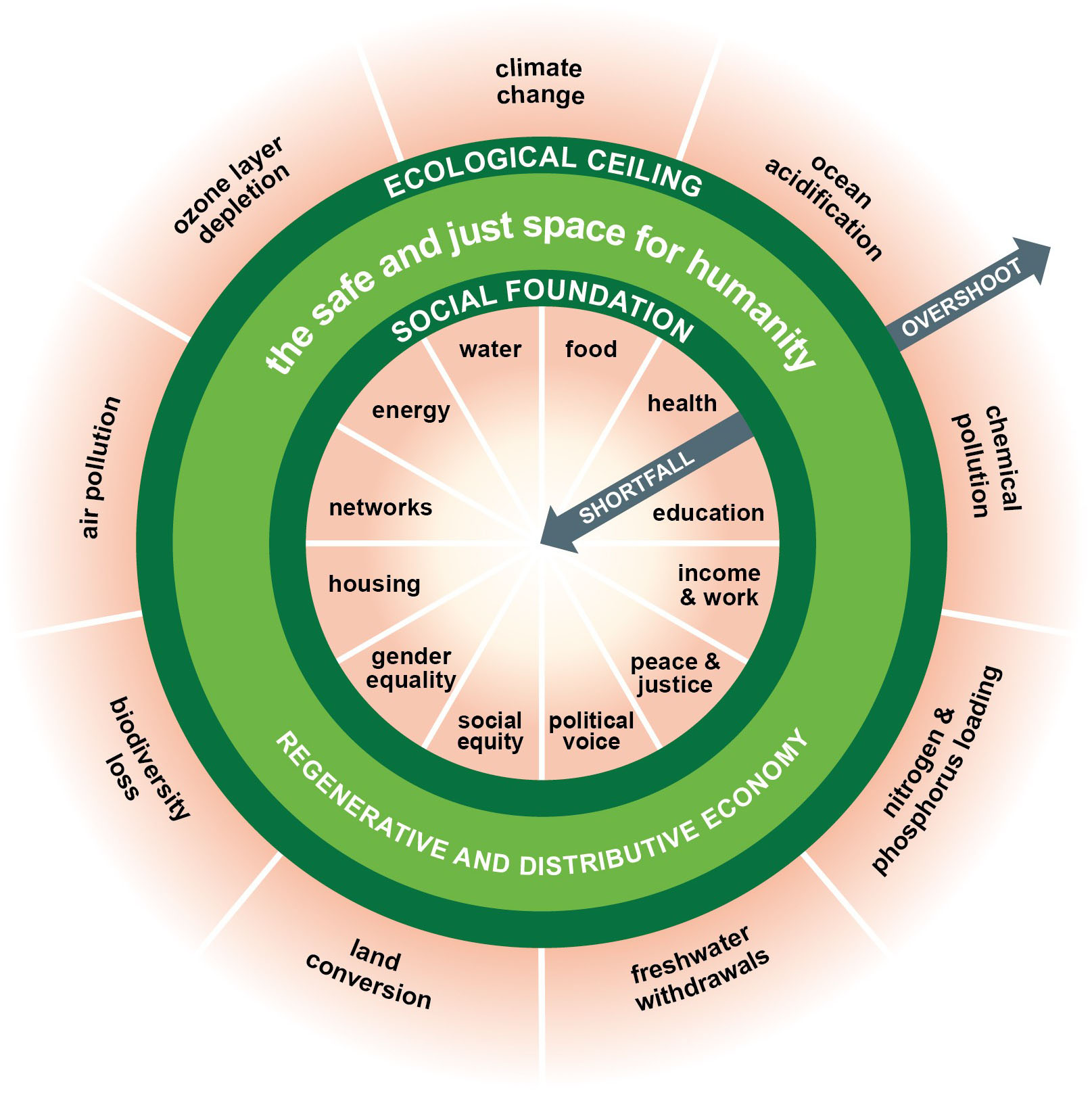
In 2017, economist Kate Raworth created a new model of human wellbeing with a donut-like framework [15]. Her model represents the environment via nine planetary boundaries, including climate change, ocean acidification, land conversion, and ozone layer depletion (see Figure 1). By linking the environment to social foundations like access to water, food, and health, Raworth attempted to identify points at which human impact could overwhelm the carrying capacity of the natural environment in ways that threaten our very existence. This framework inspired scientists to attempt to recognize feedback between humans and the environment, quantify the accompanying thresholds, and predict when society might cross them.

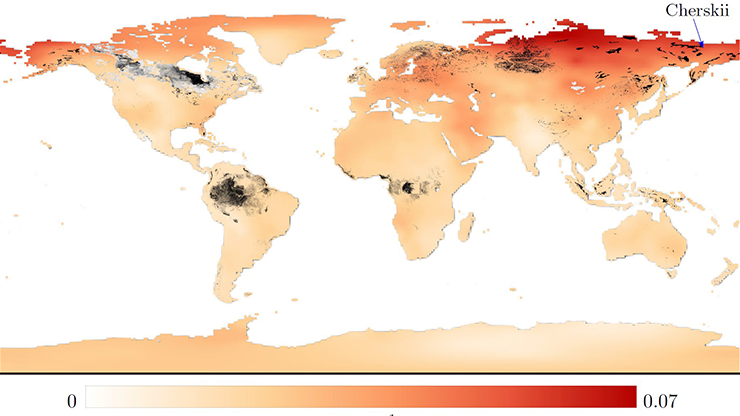
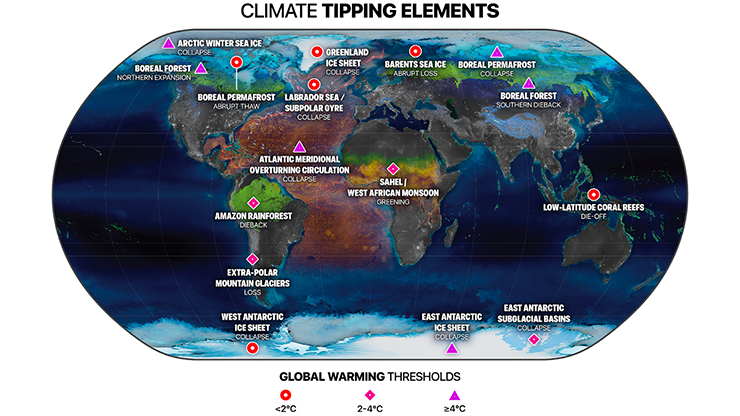
Thresholds across human-environment systems can arise in several ways. They are most predictable when they originate via linear or monotonic processes, in which case mathematics has a limited role. But sometimes they come about suddenly, which begs the question of whether tipping points can dictate some human-environment relationships — a query that requires more sophisticated mathematical tools.

Some thresholds within the donut framework do appear to manifest as tipping points, especially those that pertain to climate and ecosystem changes [3, 8]. However, researchers do not yet know whether thresholds for other planetary boundaries or social foundations manifest as tipping points; this is still an active area of research in sustainability science [5, 12]. Nonlinear feedback, abruptness, multiple stable states, and limited reversibility of changes must be present for tipping points to occur [11].

Mathematics offers clear definitions of the various ways in which a dynamical system can experience a tipping point. Bifurcation theory seeks to understand and categorize the vast number of possible transitions, beginning with Henri Poincaré’s seminal work in the 19th century [14]. It could hence impart consistency and clarity to the broader discussion among academia, the media, and the public, which suffers from confusion about what a “tipping point” actually means. The growing use of mathematical ideas in mainstream media seems to indicate that the public wants—and needs—approachable heuristics based on scientific concepts to better understand environmental issues like climate change and global pandemics. We thus expect popular mathematical vocabulary to continue to expand its reach in the coming years. Researchers should embrace and assist this process; policy change is difficult without public support, and the public will not support what it does not understand. 

Beyond its ability to clarify tipping point language, mathematics plays an important scientific role in the study of human-environment relationships that are central to many sustainability challenges. Although coupled models with separate dynamic variables for humans and their environment are relatively recent, the oldest single-variable population models exhibit an inkling of the importance of such interactions.

We can trace the first mathematical contemplation of population dynamics to 1798 when English economist Thomas Robert Malthus suggested that human populations grow exponentially until they are limited by resource availability [10]. 40 years later, Pierre-François Verhulst introduced a logistic growth model with an environmental carrying capacity that represents the regime of resource-limited growth for human populations [16]. Nearly a century later, Alfred Lotka and Vito Volterra derived logistic growth models for predator-prey systems [9, 17]. Early fishery models in the 1950s initially represented human harvest with a fixed “effort” parameter, though endogenous human dynamics replaced this fixed parameter in the 1960s. Inspired by Lotka-Volterra equations, the 1970s saw additional models to describe the coupled dynamics of small human populations and local resources. Two decades later, land use models began to account for spatial structure and localized interactions by using social and ecological data. In fact, political scientist Elinor Ostrom’s work demonstrated that human populations often use social norms to maintain common-pool resources in the absence of a central governing body, giving rise to new concepts for the coupling of human and environmental dynamics [13].

These models grew in complexity over time, but human activities were typically considered to be external forces that act on the environment. However, human behaviors and social processes both affect the environment and are dynamically influenced by it; these influenced actions then loop back to impact the environment once again. This reciprocal relationship creates complex, often nonlinear dynamics that can yield vastly different outcomes from those that are predicted when human influence is static or absent. Despite the widely recognized importance of these feedback loops, very few coupled human-environment system (CHES) models considered two-way coupling until roughly a decade ago.

We now know that several mechanisms constitute feedback loops within CHES models and human systems. In the context of public opinion dynamics and forests, for example, more public support for forest protection has a positive impact on forest health (see Figure 2). Conversely, very healthy forests can negatively impact the prevalence of pro-conservation opinion, as people may feel less urgency to act when the ecosystem is healthy; equivalently, deforestation and the consequent decrease in forest cover can inspire public demand for more sustainable forestry and thereby contribute to forest rebound. This dynamic is called rarity-based conservation [6]. The two arrows in Figure 2 collectively form a negative feedback loop that connotes stability at intermediate levels of ecosystem health between best- and worst-case scenarios.

However, people also respond to others in the population, not just the ecosystem state. If individuals tend to conform to the opinions of those around them, then injunctive social norms will reinforce the more prevalent opinion via a rapid, self-reinforcing process [2] (see Figure 2). The same population could hence end up with either high or low support for conservation, depending on its initial environmental and opinion states. As external conditions change, the mix of negative and positive feedback in the human-environment system can potentially move the system beyond a tipping point; the system may then quickly shift between opposing opinions. Such a change between states is often difficult to reverse, requiring extra effort to return to the pre-tipping condition (hysteresis). 

Newer models include several of these coupling pathways and divide human populations into subpopulations based on their environmental impact. In simple mathematical models, for example, a subpopulation of “mitigators” can change in size based on a dynamical equation that combines components—such as the influence of social norms (\(\delta)\), social learning (\(\sigma)\), and cost of mitigation (\(c)\)—into utility functions (\(\Delta U)\) (see Figure 3).

We can couple these simple models of human dynamics to models of any relevant environmental system, including forest growth, climate change, and invasive species spread. Previous studies found that this type of coupling generally leads to more regime shifts (tipping points) in the coupled systems, which are not present in uncoupled systems [7]. CHES models have found that signals from the social system can more effectively predict regime shifts than those from the environmental system. We also discovered that human feedback in the coupled model can partially mute early warning signals [1]; the increase in variance before a regime shift is smaller than in the corresponding uncoupled system. By incorporating real-time social media and economic data that monitors environmental systems into CHES models, we may improve our understanding of regime shifts.

Ultimately, CHES models involve intricate, often nonlinear feedback where the state of the environment influences human decisions and actions, and vice versa. Accounting for this dynamic coupling can thus have important consequences—sometimes surprising or counterintuitive ones—on the system’s behavior. As such, failing to consider this dynamic coupling and resulting feedback can underestimate the potential for environmental change and regime shifts. We therefore believe that simple CNES models of tipping points can serve as valuable tools for policy interventions, since policies could utilize the rich dynamics (e.g., more equilibria and thresholds) that are not present if the systems are studied in isolation [4]. However, coupling does require close integration of regulatory systems that may otherwise analyze human behavior and environmental change in different sectors.

In Canada, the recent creation of the Emergency Management Ontario program highlights the possible coordination of human behavior change across different types of environmental emergencies, such as drought, floods, forest fires, and pandemics. Similarly, an international group of scientists who comprise the International Panel on Behavior Change are developing policies to “share and make accessible key knowledge, attitudes and levers for action, universal or contextualizable, as to facilitate the emergence of a more structurally and spontaneously sustainable, desirable and equitable world.”

We believe that meeting humanity’s greatest challenges—those that demand the “rapid, far-reaching, and unprecedented changes” highlighted by the Intergovernmental Panel on Climate Change—will depend on stronger engagement with applied mathematics in cross-disciplinary and cross-sector collaborations.

Madhur Anand delivered an invited presentation on this topic at the 2024 SIAM Conference on Mathematics of Planet Earth, which took place last year in Portland, Ore.

References 
[1] Bauch, C.T., Sigdel, R., Pharaon, J., & Anand, M. (2016). Early warning signals of regime shifts in coupled human-environment systems. Proc. Natl. Acad. Sci., 113(51), 14560-14567. 
[2] Cialdini, R.B., & Goldstein, N.J. (2004). Social influence: Compliance and conformity. Annu. Rev. Psychol., 55(1), 591-621.
[3] Dakos, V., Scheffer, M., van Nes, E.H., Brovkin, V., Petoukhov, V., & Held, H. (2008). Slowing down as an early warning signal for abrupt climate change. Proc. Natl. Acad. Sci., 105(38), 14308-14312.
[4] Farahbakhsh, I., Bauch, C.T., & Anand, M. (2024). Tipping points in coupled human-environment system models: A review. Earth Syst. Dyn., 15(4), 947-967.
[5] Hao, Y., Liu, H., Li, J., & Mu, L. (2025). Environmental tipping points for global soil nitrogen-fixing microorganisms. iScience, 28(1), 111634.
[6] Henderson, K.A., Bauch, C.T., & Anand, M. (2016). Alternative stable states and the sustainability of forests, grasslands, and agriculture. Proc. Natl. Acad. Sci., 113(51), 14552-14559.
[7] Innes, C., Anand, M., & Bauch, C.T. (2013). The impact of human-environment interactions on the stability of forest-grassland mosaic ecosystems. Sci. Rep., 3, 2689.
[8] Kéfi, S., Génin, A., Garcia-Mayor, A., Guirado, E., Cabral, J.S., Berdugo, M., … Maestre, F.T. (2024). Self-organization as a mechanism of resilience in dryland ecosystems. Proc. Natl. Acad. Sci.,121(6), e2305153121.
[9] Lotka, A.J. (1925). Elements of physical biology. Baltimore, MD: Williams and Wilkins Company.
[10] Malthus, T.R. (1798). An essay on the principle of population, as it affects the future improvement of society with remarks on the speculations of Mr. Godwin, M. Condorcet, and other writers. London, England: Joseph Johnson.
[11] Milkoreit, M., Hodbod, J., Baggio, J., Benessaiah, K., Calderón-Contreras, R., Donges, J.F., … Werners, S.E. (2018). Defining tipping points for social-ecological systems scholarship — an interdisciplinary literature review. Environ. Res. Lett., 13(3), 033005.
[12] Otto, I.M., Donges, J.F., Cremades, R., Bhowmik, A., Hewitt, R.J., Lucht, W., … Schellnhuber, H.J. (2020). Social tipping dynamics for stabilizing Earth’s climate by 2050. Proc. Natl. Acad. Sci., 117(5), 2354-2365.
[13] Ostrom, E. (1990). Governing the commons: The evolution of institutions for collective action. New York, NY: Cambridge University Press. 
[14] Poincaré, H. (1885). Sur l'équilibre d'une masse fluide animée d'un mouvement de rotation. Acta Math., 7, 253-380.
[15] Raworth, K. (2017). A doughnut for the Anthropocene: Humanity's compass in the 21st century. Lancet Planet. Health, 1(2), e48-e49. 
[16] Verhulst, P.F. (1838). Notice sur la loi que la population suit dans son accroissement. Correspondence Mathematique et Physique (Ghent), 10, 113-121.
[17] Volterra, V. (1926). Fluctuations in the abundance of a species considered mathematically. Nature, 118(2972), 558-590.