Measuring Paper Thickness

As I was toying with some sheets of paper recently, the following puzzle came to mind: Given two identical sheets of paper and a tape measure, how can we estimate the paper’s thickness? The paper must remain fully undamaged, indistinguishable from its original state. No other items are available.

Here is a possible way:

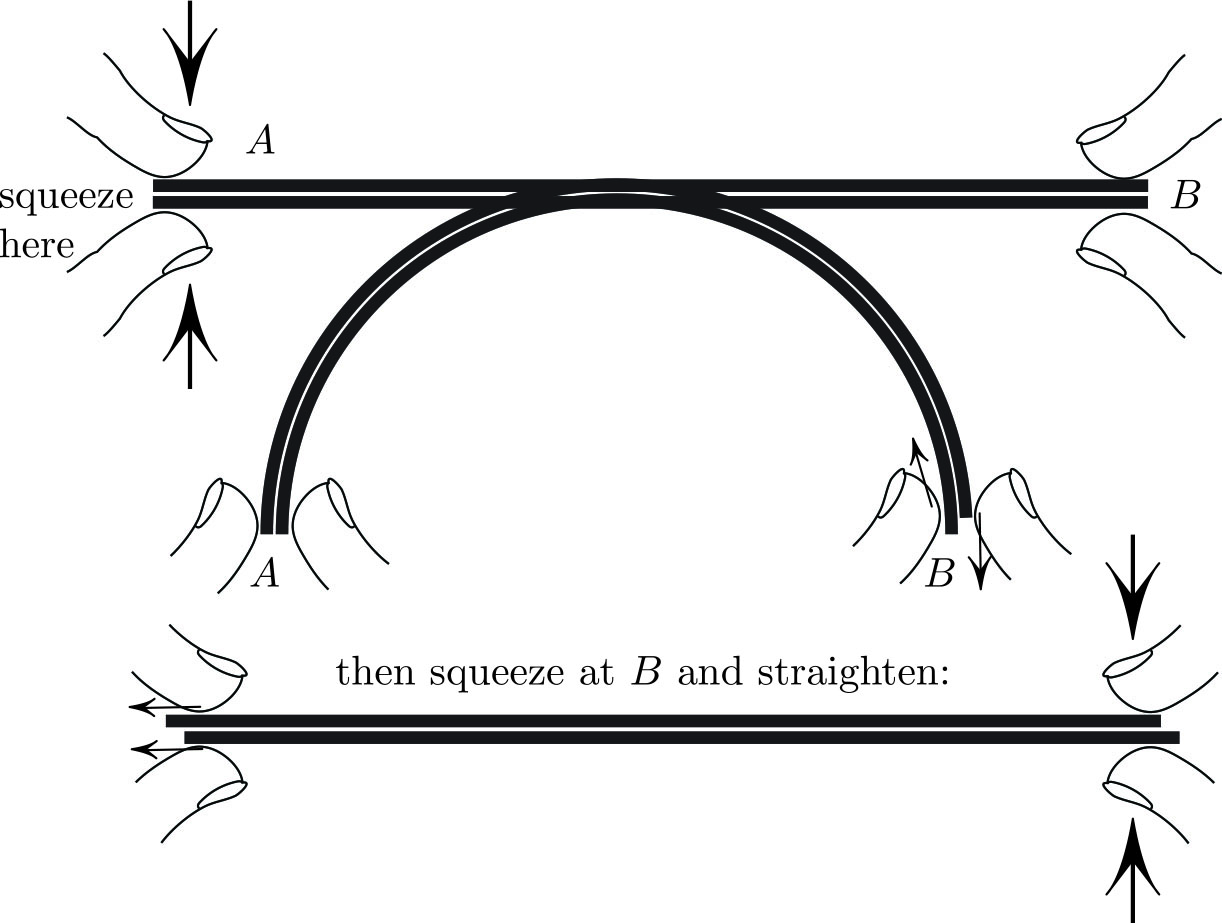
1. Stack the sheets on top of each other and squeeze them together at one end \((A)\) to prevent relative sliding (see Figure 1).
2. Bend the sheets as shown in Figure 1, allowing them to slide relative to each other at the other end \((B)\). Apply gentle sliding forces—indicated by the small arrows at \(B\)—to ensure that the sheets touch along their entire length without gaps. The ends at \(B\) will shift relative to each other by a very small amount \(\delta\), which is too small to measure with a tape measure.
3. Squeeze the sheets together at \(B\) to prevent sliding, so as to fix \(\delta\). Relax the squeeze at \(A\) and straighten the sheets; they will end up with a tiny shift \(\delta\) that is again too small to measure with a tape measure.
4. Repeat this cycle \(n\) times (with the \(n\) of your choice) to accumulate a measurable shift \(\Delta_n\), thus finding \(\delta = \Delta_n/n\) (see Figure 2).¹

We can now recover the paper’s thickness \(\varepsilon\) from the shift. It turns out that

\[\varepsilon = \frac{\delta}{\theta}, \tag1\]

where \(\theta\) is the angle by which the sheets were bent. In Figure 1, \(\theta = \pi\).

With two sheets of regular printer paper, I measured \(\Delta_3 = 1\) millimeter (mm), with an error smaller than my eye could see. Then, \(\delta =\Delta_3/3= 1/3\) yielded

\[\varepsilon \approx 0.1 \textrm{ mm},\]

the right order of magnitude (although less accurate than folding the paper into many layers and dividing the thickness of the stack by the number of layers²).

Must the bend in Figure 1 be circular? Interestingly, \((1)\) holds for any shape; the only thing that matters is the angle \(\theta\) between the tangents at the two ends.

Proof of \((1)\) for Circular Arcs

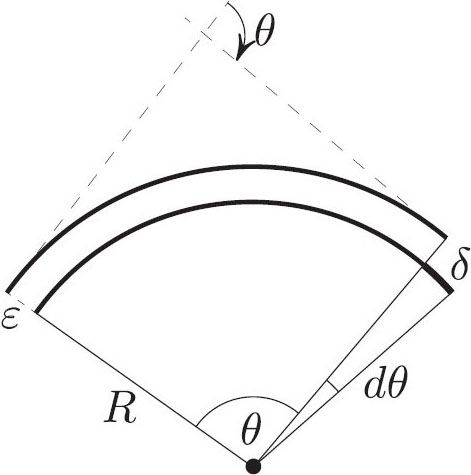
Figure 3 shows the midlines of two sheets that are bent through angle \(\theta\) into circular arcs. The thickness \(\varepsilon\) that we seek is also the distance between the sheets’ midlines. The two arcs have the same length:

\[R (\theta + d \theta ) = (R+ \varepsilon ) \theta.\]

Solving for \(\varepsilon\), we get

\[\varepsilon = \frac{R d\theta}{\theta } = \frac{\delta }{\theta},\]

as claimed.

Proof of \((1)\) for Arbitrary Arcs

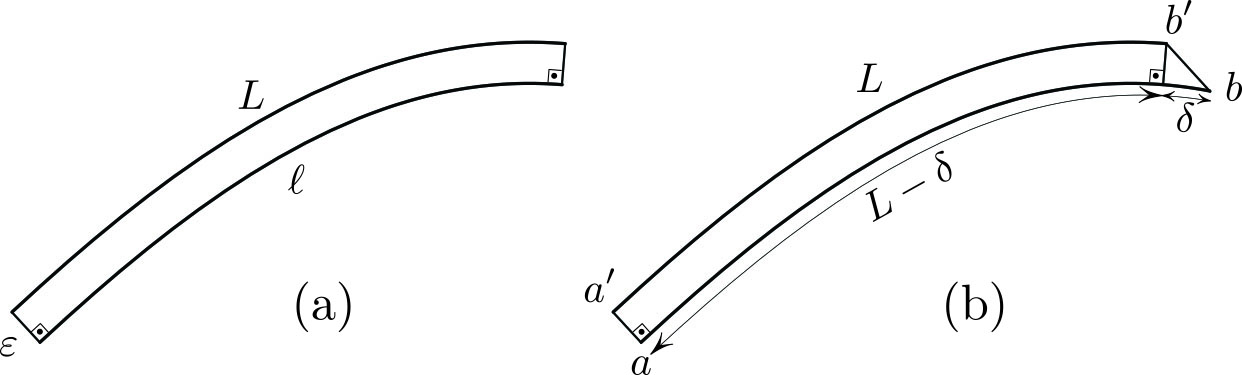
Figure 4a shows two curves that are separated by a fixed distance \(\varepsilon\). Their lengths \(L\) and \(\ell\) are related by

\[L=\ell + \varepsilon \theta, \tag2\]

where \(\theta\) is the angle between the tangents at the two ends of the curves (tangents to the two curves are parallel at the corresponding points, where correspondence means that the points lie on the common normal to both curves). Applying this remark to our two midlines in Figure 4b yields

\[L= \underbrace{(L- \delta)}_{\ell}  + \varepsilon \theta,\]

which again gives \((1)\).

Another Way

We could also prove \((1)\) for general curves by using the statement for the circular case and cutting the “railroad track” in Figure 4 into pairs of short arcs with many normal lines. We can approximate these arcs with osculating circles to which the earlier proof applies; I omit the details, mentioning only that the circular case applies because the osculating circles at the corresponding points are concentric (as follows from the fact that the distance \(\varepsilon = \textrm{const.}\)).

It may also be interesting to observe that the lines \(a a ^\prime\) and \(b b ^\prime\) in Figure 4 are almost parallel. In a linear approximation, the angle between these lines is 

\[\theta - \tan ^{-1} \theta,\]

which for small \(\theta\) is indistinguishable from zero in practice.

¹ At first glance, it may seem like the shift \(\delta\) will decrease slightly after each consecutive cycle because the overlap will shorten a bit. But this is not the case; the shift does not depend on the length of the overlap according to \((1)\).

² Of course, paper is cheap enough that we can afford to ruin a sheet by folding it into many layers and dividing the stack’s thickness by the number of layers. The method that I describe here is only a curiosity and is not meant for practical use.

The figures in this article were provided by the author.