SIAM News Blog
Research

Mechanistic Determination and Parameter Estimation for Tear Film Breakup

By

Millions of people around the world experience dry eye disease. A primary cause of this uncomfortable condition is tear film breakup, which occurs when the layer of tears on the ocular surface fails or ruptures and a thinned region forms. The tear film, which comprises mostly water, protects the surface of the eye and promotes clear vision (see Figure 1a). The film’s lipid layer prevents evaporation and its mucus layer restricts the transport of ions and foreign particles. Both tear film breakup and low aqueous tear volume—another aspect of dry eye—can lead to inflammation, blurry vision, and hyperosmolarity (a high salt concentration). Models of the mechanisms that affect the tear film and potentially instigate breakup can improve healthcare practitioners’ understanding of dry eye disease. 

Optometrists instill sodium fluorescein into patients’ eyes and image them to visualize characteristics of breakup instances, such as their shape and formation speed. In fluorescent image data, tear film breakup appears as a dark region against an otherwise green tear film (see Figure 1b) [2]. Breakup may form in as little as a few tenths of a second, though it can take up to several minutes. Slow tear film thinning is a relatively constant process that is caused by evaporation, whereas rapid breakup is hypothesized to be driven by the Marangoni effect — a highly time-dependent mechanism that induces surface tension-driven flow away from the breakup region via an increase in lipid concentration in a lipid “glob.”

<strong>Figure 1.</strong> The human tear film. <strong>1a.</strong> Simple diagram of the three-layered tear film. <strong>1b.</strong> Fluorescent tear film image with an inset of the breakup region. The grayscale, filtered, contrast-enhanced data that is extracted along the yellow line is fit with our model. Figure courtesy of Rayanne Luke; Figure 1b adapted from image by Deborah Awisi-Gyau [2].
Figure 1. The human tear film. 1a. Simple diagram of the three-layered tear film. 1b. Fluorescent tear film image with an inset of the breakup region. The grayscale, filtered, contrast-enhanced data that is extracted along the yellow line is fit with our model. Figure courtesy of Rayanne Luke; Figure 1b adapted from image by Deborah Awisi-Gyau [2].

We fit a 2019 mixed-mechanism model [9] to imaging data [5]. The model includes a combination of Marangoni tangential flow and evaporation that cause breakup on different time scales. We model the tear film as a single layer and use lubrication theory to simplify the Navier-Stokes equations, ultimately yielding leading-order partial differential equations for the conservation of mass and momentum of the tear fluid. Marangoni flow and pressure-driven flow compete with each other, as the former creates the breakup and the latter combats thinning. Osmosis slowly adds tear fluid from the cornea, and advection and diffusion transport salt and fluorescein ions within the tear film (see Figure 2). The model is designed to capture simple breakup shapes; it includes an axisymmetric version for spots and a linear version for streaks. We adapt the time scale of this model to better fit intermediate-time breakup instances that occur between one to eight seconds after a blink. Upon solving the model, we use the solutions for tear film thickness and fluorescein concentration to compute theoretical fluorescent intensity.

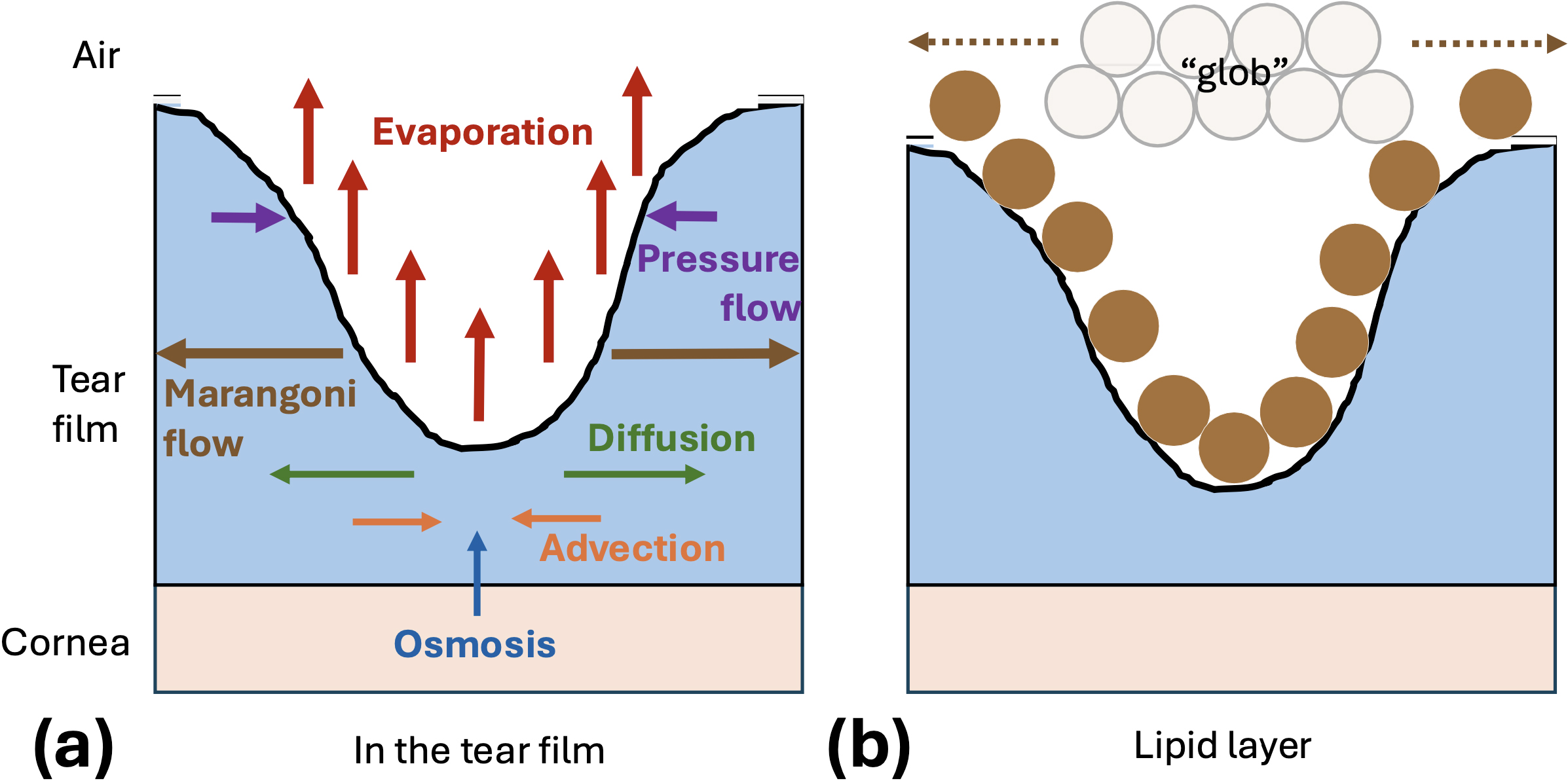
<strong>Figure 2.</strong> Schematic of the mixed mechanism model of tear film breakup. <strong>2a.</strong> The processes within the tear film. <strong>2b.</strong> Lipid surface concentration. Arrows indicate the spread of the “glob.” Figure courtesy of Rayanne Luke.
Figure 2. Schematic of the mixed mechanism model of tear film breakup. 2a. The processes within the tear film. 2b. Lipid surface concentration. Arrows indicate the spread of the “glob.” Figure courtesy of Rayanne Luke.

We extract experimental intensity data across a line that is drawn through a dark spot or streak (as in the inset in Figure 1b). We then compute initial fluorescein concentration and localized tear film thickness estimates, utilize nonlinear least squares optimization to minimize the difference between the experimental intensity and our model’s theoretical intensity, optimize over clinically relevant parameters, and calculate the corresponding osmolarity (salt ion levels), tear film thinning rates, and tear film thickness values. These quantities are especially interesting to clinicians and cannot be measured in vivo in breakup regions.

The optimization occurs over the evaporation rate, size of the lipid glob, and change in surface tension. The final optimization parameter relates directly to a nondimensional value called the Marangoni number that quantifies the strength of the Marangoni effect. We used dry lab simulations to verify the optimization procedure [4], and found it to be robust and fairly insensitive to initial guesses. Figure 3 illustrates an example fit. Here, solid lines show experimental intensity and dashed lines show its theoretical counterpart; solid and dashed lines with matching colors represent the same time level. For this fit, we find a large Marangoni number and a small evaporation rate, suggesting that rapid tangential flow (due to the Marangoni effect) drives the thinning.

<strong>Figure 3.</strong> Example fit to fluorescent image data. <strong>3a.</strong> Theoretical (dashed lines) and experimental (solid lines) intensity. <strong>3b.</strong> Corresponding model solution for tear film thickness. Figure courtesy of [5].
Figure 3. Example fit to fluorescent image data. 3a. Theoretical (dashed lines) and experimental (solid lines) intensity. 3b. Corresponding model solution for tear film thickness. Figure courtesy of [5].

Combining the effects of evaporation and lipid-driven changes in surface tension allows us to successfully fit breakup instances that occur on an intermediate time scale. In contrast, exclusion of one of the mechanisms leads to a bad fit — indicating that evaporation plays an important role in these intermediate breakup instances, and changes in surface tension may dominate rapid thinning that occurs in less than one second. We also find that the optimal evaporation rate falls within experimental ranges, and our theoretical maximum osmolarity values are largely separated by causal mechanism (see Figure 4). Because hyperosmolarity plays an etiological role in dry eye disease, this finding could be of great interest to clinicians. Importantly, we can quantify the relative sizes of the Marangoni effect and evaporation and classify breakup instances as Marangoni-dominated, evaporation-dominated, or transitional thinning.

<strong>Figure 4.</strong> Distributions of important breakup quantities. <strong>4a.</strong> Rates of change are plotted against experimental point measurements from a 2005 study [5]. The model thickness is given by \(\partial h' / \partial t'\) for either the mixed-mechanism \((M)\) version or evaporation only \((E)\) version, the latter of which is based on results from [6]. <strong>4b.</strong> Maximum theoretical osmolarity. Figure courtesy of [5].
Figure 4. Distributions of important breakup quantities. 4a. Rates of change are plotted against experimental point measurements from a 2005 study [5]. The model thickness is given by \(\partial h' / \partial t'\) for either the mixed-mechanism \((M)\) version or evaporation only \((E)\) version, the latter of which is based on results from [6]. 4b. Maximum theoretical osmolarity. Figure courtesy of [5].

By objectively quantifying various breakup measurements that cannot be measured during patient trials, we seek to understand a condition that is often diagnosed with subjective tests; subsequent research has pursued a first attempt at a population-level understanding of tear film breakup dynamics [3]. In this following work, we use a machine learning framework to automate the breakup region identification process and fit ordinary differential equation versions of the model to the center of breakup regions. These efforts yield distributions for the causal mechanisms and parameter ranges of breakup in healthy tear films. 

A related study also recently developed a model for the release of drug by a contact lens in a system with lens motion and blinking [1]. This model makes predictions about cumulative drug loss from the lens and uses physically realistic hand-tuned parameters to replicate experimental data from a 3D printed model of the eye [8]. Future work in the field of mathematical ophthalmology is poised to advance mechanistic understanding of tear film dynamics and improve ocular care.

Rayanne Luke delivered a minisymposium presentation on this research at the 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), which took place in Tokyo, Japan, last year. She received funding to attend ICIAM 2023 through a SIAM Travel Award that was supported by U.S. National Science Foundation grant DMS-2233032. To learn more about SIAM Travel Awards and submit an application, visit the online page. 

References
[1] Anderson, D.M., & Luke, R.A. (2024). Mathematical models of drug delivery via a contact lens during wear. La Mat.
[2] Awisi-Gyau, D. (2020). Characterization of tear breakup and its sensory effects [Ph.D. thesis, Indiana University]. Indiana University ProQuest Dissertations & Theses (No. 28002612).
[3] Driscoll, T.A., Braun, R.J., Luke, R.A., Sinopoli, D., Phatak, A., Dorsch, J., … Awisi-Gyau, D. (2023). Fitting ODE models of tear film breakup. Model. Artif. Intell. Ophthalmol., 5(1), 1-36. 
[4] Luke, R.A. (2021). Parameter identification for tear film thinning and breakup [Ph.D. thesis, University of Delaware]. University of Delaware ProQuest Dissertations Publishing (No. 28549566).
[5] Luke, R.A., Braun, R.J., Driscoll, T.A., Awisi-Gyau, D., & Begley, C.G. (2021). Parameter estimation for mixed-mechanism tear film thinning. Bull. Math. Biol., 83(5), 56. 
[6] Luke, R.A., Braun, R.J., Driscoll, T.A., Begley, C.G., & Awisi-Gyau, D. (2020). Parameter estimation for evaporation-driven tear film thinning. Bull. Math. Biol., 82(6), 71.
[7] Nichols, J.J., Mitchell, G.L., & King-Smith, P.E. (2005). Thinning rate of the precorneal and prelens tear films. Invest. Ophthalmol. Vis. Sci., 46(7), 2353-2361 
[8] Phan, C.-M., Shukla, M., Walther, H., Heynen, M., Suh, D., & Jones, L. (2021). Development of an in vitro blink model for ophthalmic drug delivery. Pharmaceut., 13(3), 300.
[9] Zhong, L., Braun, R.J., Begley, C.G., King-Smith, P.E. (2019). Dynamics of fluorescent imaging for rapid tear thinning. Bull. Math. Biol., 81(1), 39-80. 

About the Authors

Rayanne A. Luke

Assistant professor, George Mason University

Rayanne A. Luke is an assistant professor in the Department of Mathematical Sciences at George Mason University.

Richard J. Braun

Carl Rees Professor Emeritus of Mathematics, University of Delaware

Richard J. Braun is the Carl Rees Professor Emeritus of Mathematics in the Department of Mathematical Sciences at the University of Delaware.

Tobin A. Driscoll

UNIDEL Professor of Mathematical Sciences, University of Delaware

Tobin A. Driscoll is a UNIDEL Professor of Mathematical Sciences and director of the M.S. in Data Science program in the Department of Mathematical Sciences at the University of Delaware.