Modeling Avian Influenza: Identifiability and Epidemiology

Avian influenza occurs naturally in wild birds across the world, but infection can also spread to domestic birds and other species such as pigs, cats, and cows — and even humans in isolated cases. At this point, humans have mostly been exposed to the disease through bird-to-human transmission. “The question that arises when we look at it is, what is the possibility for spread between humans?” Omar Saucedo of Virginia Tech said. 

Saucedo hopes to monitor possible shifts in avian influenza towards easier spread from birds to humans or from humans to humans. During a minisymposium presentation at the 2025 SIAM Conference on Applications of Dynamical Systems, which is taking place this week in Denver, Colo., he discussed the mathematical modeling of avian influenza in terms of determining the model’s identifiability and finding key epidemiological measures, based on a published framework [2].

There are two forms of avian influenza to consider: low pathogenic avian influenza (LPAI) and high pathogenic avian influenza (HPAI). LPAI causes minor symptoms, such as a decrease in egg laying, but can transition to HPAI. “This is the form that we’re particularly interested in, since it’s highly deadly to domestic birds,” Saucedo said. In a previous study [1], Saucedo and collaborators focused on the competition between HPAI and LPAI when poultry are exchanged between farms, which can lead to the coexistence of different strains of the disease. The main way to control avian influenza in domestic flocks is by culling, which imposes high financial burdens. Furthermore, once a farmer realizes that a bird is sick, it has often already had an opportunity to pass the infection on to others.

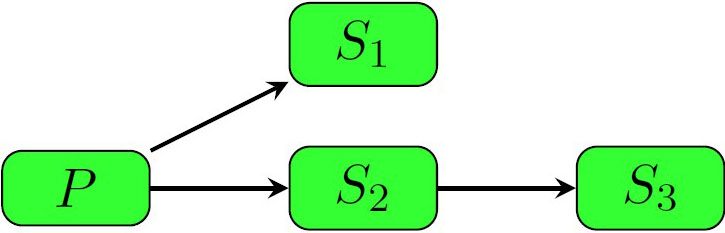
For humans, severe outbreaks of the disease with person-to-person transmission are rare and have only occurred in small pockets. The basic reproduction number ($R_0$) for avian influenza appears to be less than one in humans, so the disease dies out due to its weak transmissibility. Defining a transmission chain allows researchers to trace the secondary infections back to their primary source (see Figure 1). However, acquiring the requisite data to develop a mathematical model of the disease is a challenge, since it requires real-world tracking of infections; there are quick methods to approximate $R_0$ for new diseases, but these require data on the number of primary and secondary cases.

With mathematical models, researchers aim to make inferences from the available data and determine important modeling parameters. A key question is the identifiability of the model: when estimating the model parameters based on data, how certain can one be that they have found unique values for those parameters? Considering the type, amount, of frequency of the data all lend insights into the identifiability. In his presentation, Saucedo explored both the structural and practical identifiability of an avian influenza model.

To determine structural identifiability, one assumes that the model is correct and the data is perfect. In that case, is it possible to generate unique parameter sets, i.e., obtain unique values for the unknown model parameters based on the available observations? Using an input-output equation, one tries to solve the system in terms of its parameters; every single parameter must be identifiable to say that the model itself is structurally identifiable. This process is often too complicated to do by hand. “Fortunately for us, there are multiple softwares that allow us to do this,” Saucedo said, specifically noting COMBOS, DAISY, SIAN, Julia, and GenSSI.

Saucedo dove into the structural identifiability of the model of avian influenza dynamics, which makes the strong assumption that humans can be infected both by birds and by other humans. Based on data on cumulative incidence, secondary cases, and death, he investigated whether it was possible to come up with estimates for multiple model parameters. Two separate software approaches indicated that several of the parameters were nonidentifiable, meaning that the model itself was also structurally nonidentifiable.

“Just because your system is nonidentifiable doesn’t mean that it’s all over,” Saucedo said. “There are things that you can do to mitigate that.” He was able to resolve the issue by fixing one parameter at a time and then rerunning the identifiability procedure. Ultimately, Saucedo obtained the fitted parameters and determined that $R_0<1$ in humans and $R_0>1$ in birds, which makes sense given the observed transmission of avian influenza.

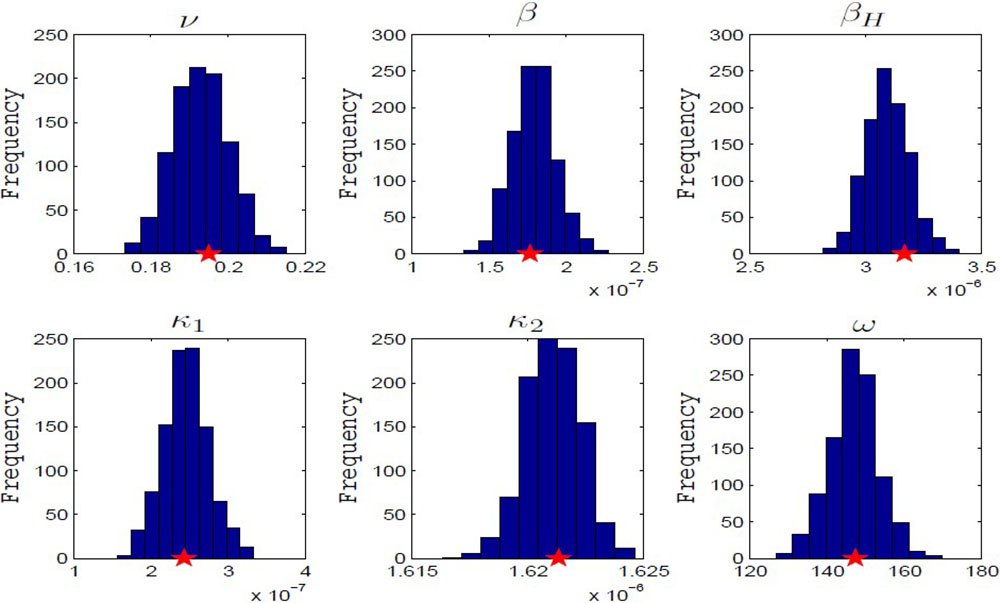
Structural identifiability analysis has the benefit of aiding in experimental design, though it also encounters the drawbacks of being complicated to perform and making the unrealistic assumption that the data is known perfectly at all times. Saucedo also discussed practical identifiability, which assumes that the underlying model is correct but that there is unavoidable noise in the data. The main way to determine practical identifiability is through a bootstrapping algorithm, which slowly adds noise to the data and then refits numerous times over to see the effect on the parameter values. Figure 2 provides histograms of the results for the avian influenza model, in which the true parameter values mostly fell in the middle of the distributions of the parameter estimates from bootstrapping.

“Identifiability analysis gives you some insight into how to work with the model and determine if parameters can be identified,” Saucedo said in summary. In the future, he intends to use these findings to influence the design of further experiments on avian influenza.

References 
[1] Saucedo, O., & Martcheva, M. (2017). Competition between low and high pathogenicity avian influenza in a two-patch system. Math. Biosci., 288, 52-70.
[2] Saucedo, O., Martcheva, M., & Annor, A. (2019). Computing human to human avian influenza $R_0$ via transmission chains and parameter estimation. Math. Biosci. Eng., 16(5), 3465-3487.