New Mathematical Developments Drive Innovations in Bioartificial Organ Design

Bioartificial organ design combines biology, engineering, and mathematics to create functional implants that support or replace natural human organs. The practice utilizes an approach called cell encapsulation, which embeds therapeutic cells in a poroelastic scaffold and encloses them in a semi-permeable membrane (see Figure 1). This process protects cells from immune rejection while allowing for nutrient and oxygen exchange, ultimately enabling long-term function without immunosuppression (e.g., in a bioartificial pancreas for the treatment of diabetes).

Ensuring cell survival over time is a major challenge, especially given the limited availability of oxygen — the key factor that affects viability. Scaffold elasticity, porosity, and architecture strongly impact oxygen and nutrient transport; to account for this influence, recent designs use vertically drilled ultrafiltrate channels to improve oxygen delivery to cells in the poroelastic scaffold. Unfortunately, hypoxic regions persist [3].

This limitation highlights the need for advanced mathematical approaches that optimize scaffold design to enhance oxygen delivery. A robust model that properly addresses this requirement must capture the following three elements: (i) the flow of blood plasma and oxygen transport within the poroelastic scaffold, (ii) the scaffold’s encapsulation within semi-permeable poroelastic membranes or plates, and (iii) the encapsulated scaffold’s integration with a vascular graft that delivers oxygen-rich blood to the transplanted cells while removing insulin and metabolic waste.

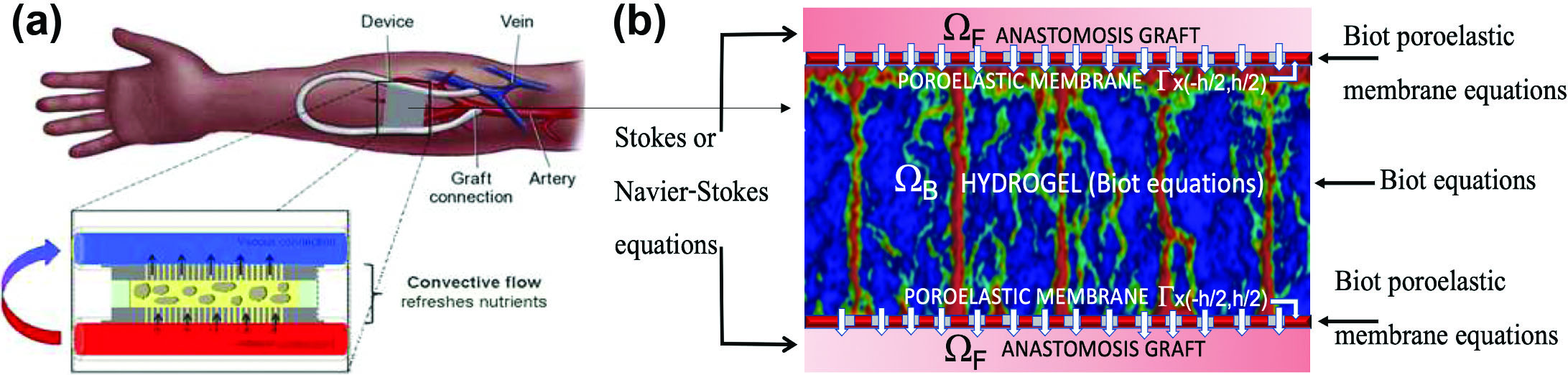
Figure 1a depicts a bioartificial pancreas implant in a patient’s arm. An anastomotic graft connects the encapsulated scaffold—which houses insulin-producing \(\beta\) cells—to the patient’s vasculature. Accurate modeling of fluid-structure interaction (FSI) between blood flow in the graft and blood plasma filtration through the poroelastic encapsulating membrane and scaffold helps predict oxygen delivery and capture the bioartificial pancreas’ mechanistic function.

The Mathematical Approach

To study cell encapsulation, we are developing a comprehensive multiscale and multiphysics framework that incorporates state-of-the-art mathematical and computational methods. The framework utilizes the following four modules:

(I) A macroscale FSI module models the interaction between blood flow through the anastomosis graft—via the Stokes or Navier-Stokes equations—and the encapsulated poroelastic scaffold (see Figure 1b). We represent the encapsulated organ as a multilayered poroelastic medium that comprises a thin membrane (modeled via reduced Biot membrane/plate equations [8]) and a thick poroelastic hydrogel scaffold (modeled via nonlinear Biot equations [10]). Both Biot components track pore pressure, Darcy velocity, and structural displacement. Permeability coefficients depend on microstructure [1, 4, 10]; two-way coupling conditions link the fluid and poroelastic subproblems [1, 7].

Our mathematical analysis establishes the existence and stability of weak finite-energy solutions for this new FSI model, advancing the theory of FSI with poroelastic media [1, 6]. These weak solutions serve as the backbone for finite element method (FEM)-based computational solvers. To simulate the model, we developed both monolithic and partitioned schemes [9, 10] that produce fluid velocity and poroelastic structure displacement, which feed into oxygen transport modeling.

(II) A macroscale advection-reaction-diffusion module uses advection-reaction-diffusion equations to characterize oxygen- and glucose-dependent insulin release within the encapsulated poroelastic hydrogel. It links microscale processes like oxygen consumption and insulin secretion to macroscale transport; the fluid velocities from the previous module drive advection. We define the equations on moving domains; incorporate hydrogel poroelasticity, which significantly affects transport; and generate a novel FEM-based solver to efficiently simulate the fully coupled system [10].

(III) A micro/nanoscale module employs smoothed-particle hydrodynamics (SPH) to model local hydrogel structure/architecture and plasma filtration at the micro/nanoscale. These simulations allow us to recover the spatially varying macroscale permeability tensor for use in the aforementioned FSI model [10].

(IV) An artificial intelligence module utilizes an encoder-decoder convolution neural network (CNN) to efficiently estimate macroscale properties—such as the spatially varying permeability tensor—from micro/nanoscale hydrogel simulations. Instead of running costly SPH simulations online, we train the CNN on synthetic data offline to rapidly predict permeability for new architectures — including those from fabricated hydrogels. The predicted permeability tensor parameters feed into the FSI model, influencing oxygen transport results.

Results

Using the four modules, we developed FEM-based solvers [2, 9, 10] to simulate blood flow and oxygen transport in an implantable bioartificial pancreas (iBAP) prototype manufactured in the Biodesign Laboratory at the University of California, San Francisco. Figure 2a depicts the iBAP prototype during implantation in a porcine model. The device connects to an artery for blood inlet and to a vein at the outlet; pressure difference drives flow through the channel. Semipermeable silicon membranes connect the channel to poroelastic scaffolds (i.e., islet chambers) and filter plasma into the hydrogel scaffold, where transplanted islets absorb nutrients and release insulin.

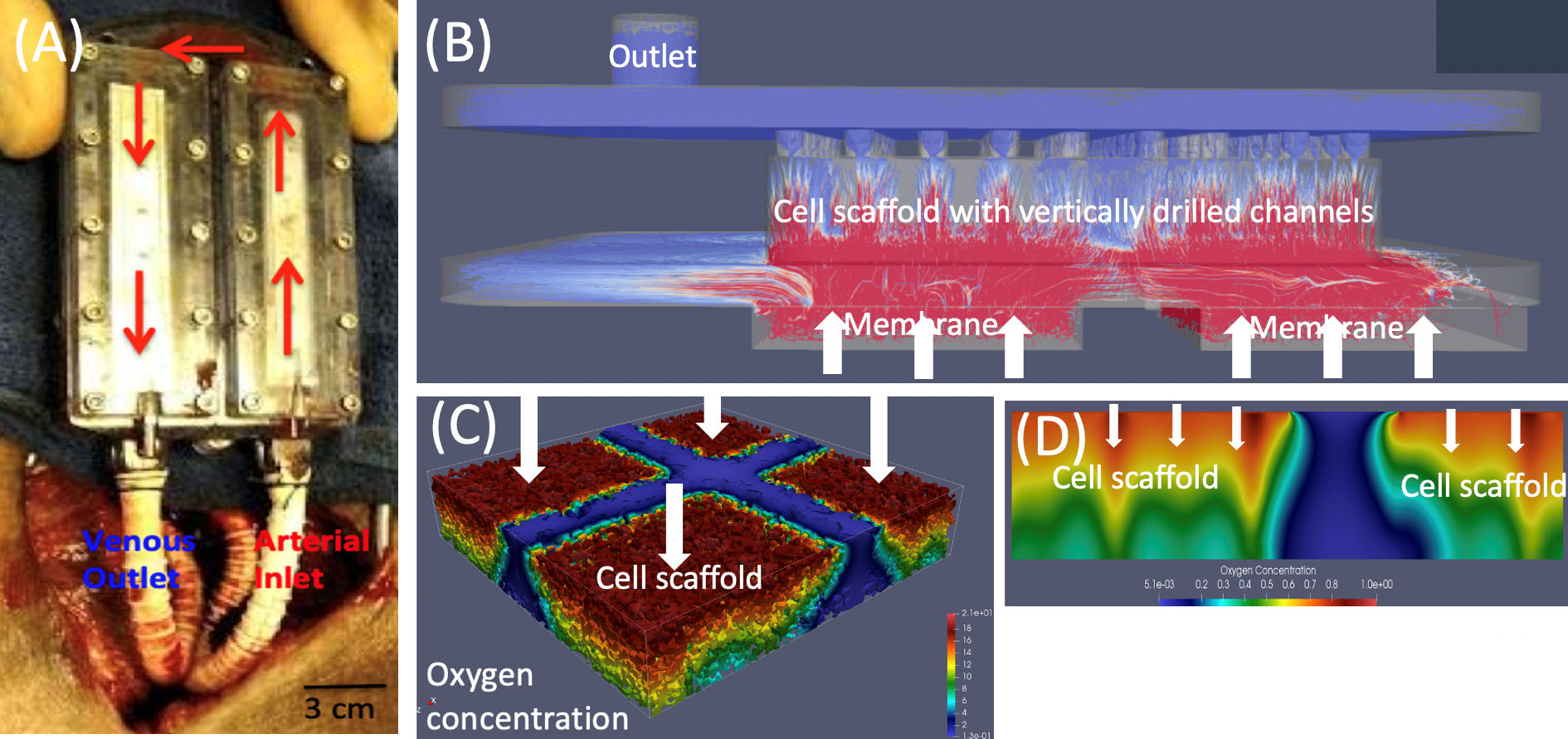
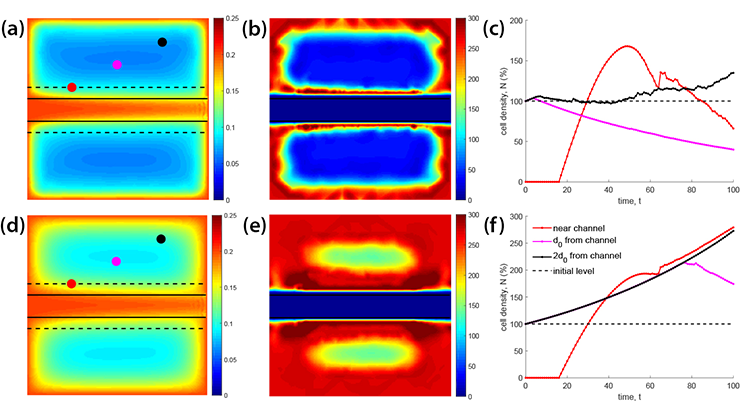
Figure 2b illustrates simulated flow through one chamber. The results of our FSI solver and scaffold microarchitecture data reveal strong filtration flow near the membranes/inlet and drilled channels, suggesting that oxygen levels are highest in these regions. Indeed, simulations with the advection-reaction-diffusion solver indicate a high oxygen concentration near the inlet and vertical channels, with hypoxic regions near the outlet where oxygen falls below the survival threshold (see Figures 2c and 2d).

To improve oxygen concentration in the cell chamber, we investigated different hydrogel scaffold architectures and produced an architecture with ultrafiltrate channels that provides oxygen concentration that is (i) as uniform as possible throughout the scaffold and (ii) above the minimum concentration at which hypoxia occurs. For this purpose, we developed a computational algorithm that employs a diffuse interface approach to solve the corresponding multiphysics problem that couples the time-dependent Stokes equations—which govern blood plasma flow through the channel network—with the time-dependent Biot equations, which characterize the Darcy velocity of blood plasma, pressure, and displacement within the poroelastic hydrogel scaffold. We subsequently utilized the calculated plasma velocity to determine oxygen concentration within the scaffold via a diffuse interface advection-reaction-diffusion model [2].

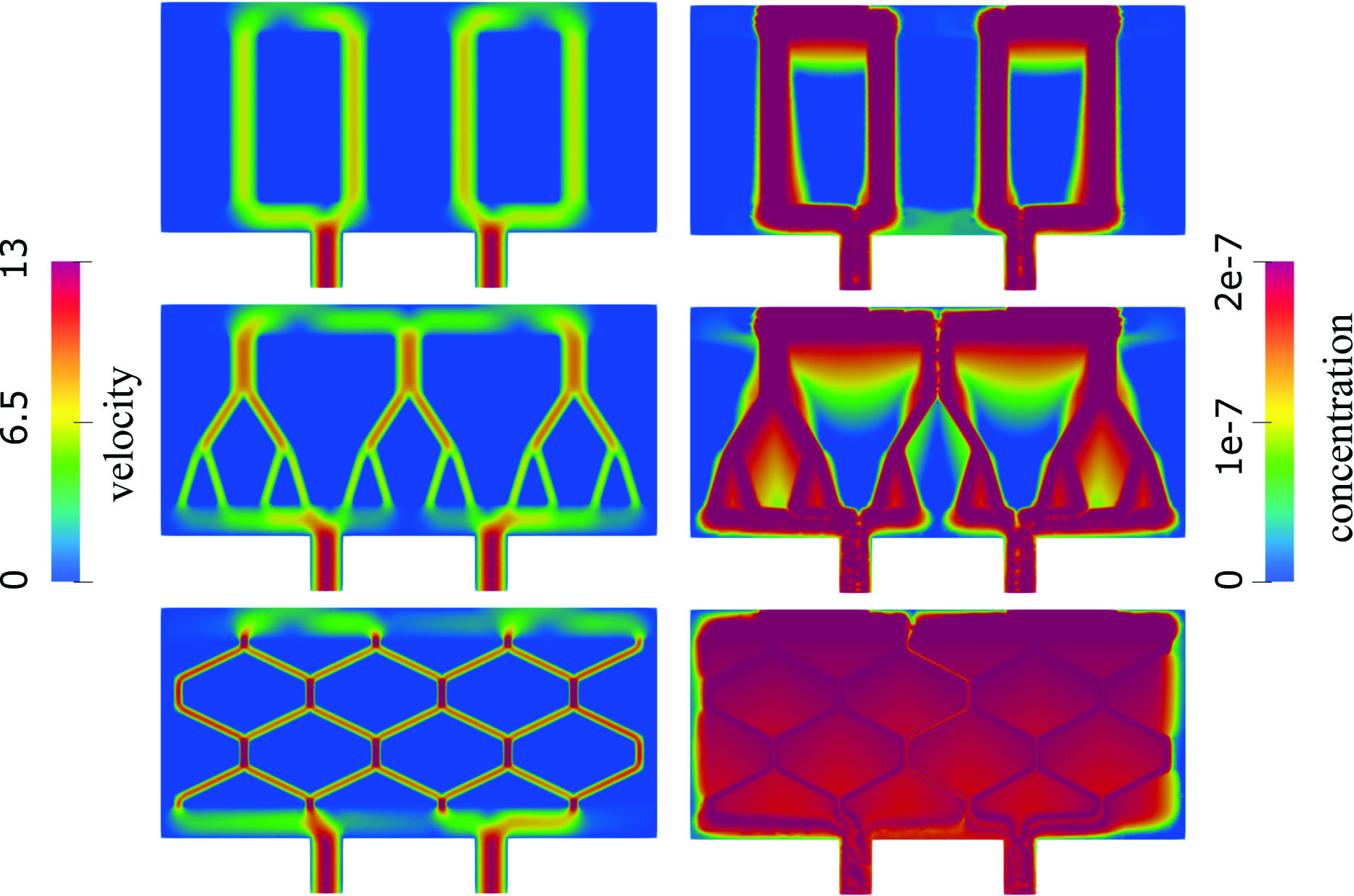
Next, we considered three scaffold architectures that are inspired by biological flow-nutrient scenarios: (i) vertical ultrafiltrate channels, the standard in bioartificial pancreas design; (ii) bifurcating channels that are modeled after vascular branching; and (iii) hexagonal channels that mimic interstitial flow in epithelial tissues. For the sake of comparison, we generated all geometries with the same total channel volume. Figure 3 shows velocity and oxygen concentration for the three cases. Most flow in vertical channels occurs within the channels, leaving hypoxic regions in between. In bifurcating networks, higher velocities appear in the first two generations of branches, leading to improved but still incomplete oxygenation between vessels. Channels in the hexagonal geometry (see Figure 3) have the smallest radius, the highest fluid velocity, and are uniformly distributed throughout the scaffold. The resulting Darcy velocity is consequently significant across the entire poroelastic hydrogel, yielding a nearly uniform oxygen distribution that is well above the critical threshold. This outcome ensures adequate oxygen delivery throughout the hydrogel and sustains normal insulin production.

Ultimately, our findings indicate that hydrogel scaffolds with hexagonal geometry (extruded in the third dimension) are more effective than the conventional vertical channel designs in current hydrogel architectures. These results are particularly significant given recent advances in hydrogel fabrication, which now permit the fine-tuned modulation of hydrogel rheological properties [5] and enable the translation of computational predictions into physically optimized scaffold designs.

Acknowledgments: The authors would like to acknowledge Boris Muha of the University of Zagreb; Jeffrey Kuan of the University of Maryland, College Park; Martina Bukac of the University of Notre Dame; and the bioengineers in Shuvo Roy’s Biodesign Laboratory at the University of California, San Francisco, for their contributions to this project. The research is also supported in part by the U.S. National Science Foundation under grants DMS-2408928, DMS-2247000, DMS-2247001, and DMS-2011319.

References
[1] Bociu, L., Čanić, S., Muha, B., & Webster, J.T. (2021). Multilayered poroelasticity interacting with Stokes flow. SIAM J. Math. Anal., 53(6), 6243-6279.
[2] Bukač, M., Čanić, S., Muha, B., & Wang, Y. (2024). A computational algorithm for optimal design of bioartificial organ scaffold architecture. PLoS Comput. Biol., 20(11), e1012079. 
[3] Kanani, D.M., Fissell, W.H., Roy, S., Dubnisheva, A., Fleischman, A., & Zydney, A.L. (2010). Permeability-selectivity analysis for ultrafiltration: Effect of pore geometry. J. Memb. Sci., 349(1-2), 405-410.
[4] Kim, S., Feinberg, B., Kant, R., Chui, B., Goldman, K., Park, J., … Roy, S. (2016). Diffusive silicon nanopore membranes for hemodialysis applications. PLOS One, 11(7), e0159526.
[5] Krishani, M., Shin, W.Y., Suhaimi, H., & Sambudi, N.S. (2023). Development of scaffolds from bio-based natural materials for tissue regeneration applications: A review. Gels, 9(2), 100.
[6] Kuan, J., Čanić, S., & Muha, B. (2023). Existence of a weak solution to a regularized moving boundary fluid-structure interaction problem with poroelastic media. Comptes Rendus Mecanique, 351(S1), 505-534.
[7] Kuan, J., Čanić, S., & Muha, B. (2024). Fluid-poroviscoelastic structure interaction problem with nonlinear coupling. J. Math. Pures Appl., 188, 345-445. 
[8] Mikelić, A., & Tambača, J. (2019). Derivation of a poroelastic elliptic membrane shell model. Appl. Anal., 98(1-2), 136-161. 
[9] Scharf, A., Bukač, M., & Čanić, S. (2025). A partitioned scheme for FSI with multi-layered poroelastic structures. Under review. 
[10] Wang, Y., Čanić, S, Bukač, M., Blaha, C., & Roy, S. (2022). Mathematical and computational modeling of poroelastic cell scaffolds used in the design of an implantable bioartificial pancreas. Fluids, 7(7), 222.